13.15: The Bohr Model of the Atom
( \newcommand{\kernel}{\mathrm{null}\,}\)
The Structure of the Atom
By the late nineteenth century, most people had accepted Dalton's proposal of 1808 that matter was made of atoms. Dalton "proved" his theory with a number of assumptions, each of which is either factually wrong or was used in a logically inconsistent manner. Nonetheless opposition from critics such as Mach, who never believed in atoms, was largely ignored. Throughout the nineteenth century atomism became an idea that came to dominate thought in a number of fields, including political science, sociology, psychology, biology and more.
 Then, in 1897 J.J. Thomson discovered the electron. He determined that these electrons had a negative electric charge and compared to the atom had very little mass. Thus he proposed that atoms consisted of a large massive positively charged body with a number of small negatively charged electrons scattered throughout it. The total charge of the electrons exactly balanced the positive charge of the large mass, so the total electric charge was zero. This was called the plum pudding model of the atom. The number of electrons determines the particular chemical element. Hydrogen, for example, has one electron; helium has two; carbon has six, etc.
Then, in 1897 J.J. Thomson discovered the electron. He determined that these electrons had a negative electric charge and compared to the atom had very little mass. Thus he proposed that atoms consisted of a large massive positively charged body with a number of small negatively charged electrons scattered throughout it. The total charge of the electrons exactly balanced the positive charge of the large mass, so the total electric charge was zero. This was called the plum pudding model of the atom. The number of electrons determines the particular chemical element. Hydrogen, for example, has one electron; helium has two; carbon has six, etc.
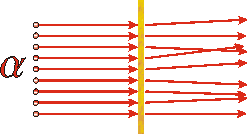
In the early twentieth century Rutherford was experimenting with one of the newly discovered radioactive substances, one that emitted alpha particles. He knew that these particles had a mass much larger than the electron and had a net positive electric charge; now we know that these particles are identical to the nucleus of the helium atom. He was directing a beam of these alpha particles onto a very thin piece of gold foil. If Thomson's plum pudding model was correct, the experiments would be sort of similar to firing BB's from a BB gun into a thin slab of cream cheese with chives. And in fact the results of Rutherford's experiments usually followed this model: almost all of the alpha particles emerged on the other side slightly deflected by their interaction with the gold. However, once in a while he observed an alpha particle that was scattered right back towards the radioactive source.
|
The above diagram shows what we would expect the result of Rutherford's experiment to be if the "plum pudding" model of the atom is correct. |
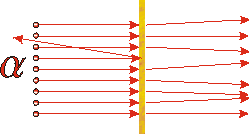
The above indicates the actual result. Most of the alpha particles are only slightly deflected, as expected, but occasionally one is deflected back towards the source. |
If you were doing the experiment involving the BB's and the cream cheese and occasionally had a BB scattered back towards you, you would probably conclude that there was something fairly small and very massive inside the slab. Similarly, Rutherford concluded that inside the gold foil there must be something fairly small, very massive, and positively charged. Thus the plum pudding model of the atom collapsed: most of the mass and the positive charge of the atom was concentrated into a very small volume. This small massive positively charged object is called the nucleus.
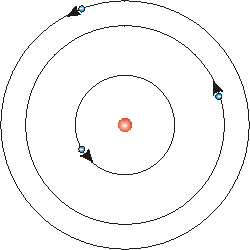 Soon, people proposed a planetary model of the atom. The electrons were in orbits around the nucleus, held in their orbits by the electric force that attracts negatively charged electrons to the positively charged nucleus.
Soon, people proposed a planetary model of the atom. The electrons were in orbits around the nucleus, held in their orbits by the electric force that attracts negatively charged electrons to the positively charged nucleus.
However this model makes no sense. We know from classical electromagnetic theory that any charged body that is in a state of motion other than at rest or in uniform motion in a straight line will emit energy as electromagnetic radiation. Thus the electrons is this planetary model will be radiating energy. As they lose energy they will spiral into the nucleus and in a matter of nanoseconds will collide with it. Thus this atom can not be stable.
Bohr's Model
Neils Bohr knew about all of these facts, and in the early part of the century was collaborating with Rutherford. He also knew about the existence of line spectra from chemical elements; a document on this topic may be found here. He was struggling to make sense of all of this. As was common with Bohr when confronted with a puzzle, this struggle was nearly all-consuming.
Then in 1913 Bohr, by accident, stumbled across Balmer's numerology for the hydrogen spectrum, and in a flash came up with a workable model of the atom. The model asserts that:
- The planetary model is correct.
- When an electron is in an "allowed" orbit it does not radiate. Thus the model simply throws out classical electromagnetic theory. Technical note: an allowed orbit is one in which the electron mass times its speed times the radius of the orbit is equal to a positive integer n times Planck's constant divided by 2 pi. The integer n can be 1, 2, 3, 17, 108, etc. In fact, there are an infinite number of allowed orbits corresponding to the infinite number of positive integers.
- When an electron absorbs energy from incident electromagnetic radiation, it "quantum jumps" into a higher energy allowed state. This higher energy state corresponds to an allowed orbit with a higher value of the integer n.
- When an electron is in a higher energy state, it can quantum jump into a lower energy state, one with a smaller value of n, emitting all of its energy as a single photon of electromagnetic energy.
A Flash animation of Bohr's model showing the excitation and photon emission of the electron in a Hydrogen atom has been prepared. It requires the Flash player of Version 6 or better; the player is available free from http://www.macromedia.com/. The file size is 74k, and the animation will appear in a separate window. To access the animation click here.
![]() Technical note: the allowed orbits are given by the equation to the right, where m is the mass of the electron, v is its speed, r is the radius of the orbit, and h is Planck's constant.
Technical note: the allowed orbits are given by the equation to the right, where m is the mass of the electron, v is its speed, r is the radius of the orbit, and h is Planck's constant.
As Bohr fully realised, this model is largely ad hoc, if not downright ugly. It does, however, "explain" the line spectra of the elements.
When Bohr published his model Otto Stern, who was Einstein’s student, and Max von Laue, who was Planck’s student, made an earnest vow: "If this nonsense of Bohr should in the end prove to be right, we will quit physics!"
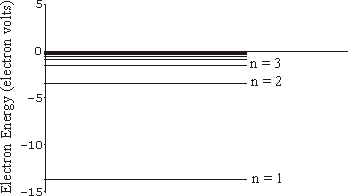 Given these assertions plus the standard classical laws of attraction between two oppositely charged objects one can calculate the energy of the electrons in their orbits as a function of the value of n. It turns out to depend on the mass and charge of the electron, Planck's constant, some constants from electromagnetic theory, and also depends on 1/n2. The energy of allowed orbits for hydrogen is shown to the right; we have also indicated the value of n for three of those energy levels.
Given these assertions plus the standard classical laws of attraction between two oppositely charged objects one can calculate the energy of the electrons in their orbits as a function of the value of n. It turns out to depend on the mass and charge of the electron, Planck's constant, some constants from electromagnetic theory, and also depends on 1/n2. The energy of allowed orbits for hydrogen is shown to the right; we have also indicated the value of n for three of those energy levels.
Technical note: the fact that the energies are negative is only due to a common convention as to where we choose the zero point of energy in a non-relativistic analysis.
Recall Balmer's formula:
![]()
Here R is a constant equal to about 10,970,000 and n is any integer greater than 2, such as 3, 4, 5, 108, etc. Each different value of n gives the wavelength of a different line in the Hydrogen spectrum. The constant R is usually called the Rydberg constant.
The wavelengths described by this formula correspond exactly to the radiation emitted when an electron in the Bohr model quantum jumps from a high energy orbit, described by some n greater than 2, to an orbit whose value of n is equal to 2. In the model transitions to other "final" states such as n equal to 1 or 3, 4, 5, etc. are also predicted and the wavelengths in the spectrum for these are found experimentally to exist. Further, the constant R turns out to be expressed in terms of fundamental physical constants. So we have pushed the numerology of Balmer's work a bit back.
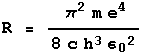 Technical note: the Rydberg constant is given by the equation to the right, where m is the mass of the electron, e its charge, c is the speed of light, h is Planck's constant, and
Technical note: the Rydberg constant is given by the equation to the right, where m is the mass of the electron, e its charge, c is the speed of light, h is Planck's constant, and ![]() the constant relating the forces exerted by charged bodies on each other and the magnitudes of the charges.
the constant relating the forces exerted by charged bodies on each other and the magnitudes of the charges.
The lowest energy allowed orbit, the one with n equal to one, is the ground state of the atom. An unexcited hydrogen atom will have its electron in this state.
Explaining the Bohr Model
In 1924 Louis de Broglie proposed that electrons have a wave nature. As part of that proposal he also described the relationship between the wavelength of the wave aspect and the mass and speed of its particle aspect. The proposal has been experimentally confirmed and is one of the fundamental aspects of Quantum Mechanics.
Imagine a planetary model of the atom, but now think of the electrons as waves. Which waves states might be allowed?
You may recall that waves that "fit" into their available space, standing waves, are the ones that are allowed. A document discussing this is available here.
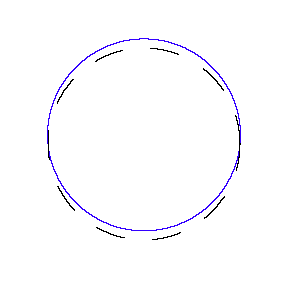
We show some of the standing waves that can exist for a circular orbit.
So in general the circumference equals n times the wavelength, where n is any positive integer. In the above figures the value of n is 1, 2 and 3 respectively.
You can view a simple animation of any of the three orbits above by pointing at it and clicking the left button. If you are using a fairly modern browser the animation will appear in a separate window; close that window whenever you wish. If you are using an older browser the animation will appear in this window; use the Back button of your browser to return here.
It turns out that these standing wave states for electrons correspond exactly to the "allowed" electron orbits in Bohr's model. So, Quantum Mechanics explains Bohr's ad-hoc model of the atom.
Now we call the integer n the principle quantum number. Note that for the hydrogen atom it completely describes the state of the electron.
"We are tracing the description of natural phenomena back to combinations of pure numbers which far transcends the boldest dreams of the Pythagoreans." -- Bohr
Tags recommended by the template: article:topic
Author
This document was written in March 1999 by David M. Harrison, Department of Physics, University of Toronto, mailto:harrison@physics.utoronto.ca. This is version 1.10, date (m/d/y) 11/19/07.
This document is Copyright © 1999, 2000, 2001, 2003 David M. Harrison.
This material may be distributed only subject to the terms and conditions set forth in the Open Content License, v1.0 or later (the latest version is presently available at http://opencontent.org/opl.shtml).