1.1: To c or Not to c
( \newcommand{\kernel}{\mathrm{null}\,}\)
Einstein’s famous special theory of relativity has gained unquestioned acceptance in the scientific world. It has been proved in countless ways and is the foundation upon which gravitation and high-energy quantum physics are based. Is it something that a “normal” person can understand? Relativity forces us to abandon our ideas about time, which is a hard thing to do, but the basic mathematics of it are relatively simple—just a picture away.
The picture depends on extending something you know about on an intuitive level. Suppose I tell you that you have an hour to drive and that you must go south at 50 miles/hour. Can you tell me where you will end up?* Suppose I tell you to go south at 100 miles/ hour: Where will you find yourself after one hour?† Suppose I tell you to go south for two hours at 50 miles/hour, where do you end up?‡ So you see, you know the distance traveled if you know how fast you are going and how much time is allowed. That is,
distance traveled is velocity × time.
Let’s check this against our intuition for the last case:
100 \text { miles }=50 \text { miles/hour } \times 2 \text { hours. }^§ \nonumber
But I’m a slow typist so I want to abbreviate this understanding by using the first letter of each word:
d=v t. \nonumber
Any heart attacks yet? Well that one relation, which you already understand enough to do the calculation in your head, is all the math you need to do much of relativity!
Note
* Fifty miles south of your start. In my case, Salem, Oregon.
† On the way to jail.
‡ One hundred miles south of your start. In my case, Eugene, Oregon.
§ Of course, the 50 × 2 on the right-hand side gives 100, the numerical part of the result on the left-hand side, but also notice that the hour in “2 hours” cancels the hour in “miles/hour” (or “miles per hour”) leaving just “miles” as the unit of the result—correctly a unit of distance. Another way to say this is “hour/hour = 1,” and 1 times anything just gives that thing back.
It’s About Time!
You are at the airport trying to catch a plane you are late for. As you run onto Concourse E, the announcer says the jetway door will be closing in 1 minute, and you see the door 300 meters (328 yards) away. With your luggage you can only run at 3 meters per second (3 m/s is 6 miles/hour), which means that it will take you 100 seconds to get to the plane, but you only have 60 seconds before the door closes. You notice a sliding walkway (slidewalk) ahead with people standing still relative to it, yet moving at the same velocity you are (3 m/s) relative to the hallway. What would you do? If you run onto the slidewalk, past the people standing still relative to the slidewalk, how fast would you be moving relative to the hallway? Would this solve your problem?*
You know that these sorts of gadgets are irresistible to children. What is the first thing a child will do on a slidewalk (or on an escalator)? Run in the “wrong” direction at 3 m/s. If she does so, what would her velocity be relative to the hallway?† She is playing with the idea that in our everyday experience, velocities add and subtract. (This is why we must use the term velocity rather than speed whenever we wish to be mindful of directions, since the latter is only the size of the velocity with no indication of direction. If direction is immaterial, speed and velocity are often used interchangeably.)
During the late 1800s, physicists were trying to find how fast the Earth was moving through a cosmic substance that they called ether.‡ They thought that they could determine the Earth’s speed (like the slidewalk’s) by comparing the speed relative to the ether (akin to the hallway) of one beam of light cast one way from the Earth to another beam of light cast sideways from that direction. But every time they tried this, they found no difference for the two cases.
This was a big mystery. Albert Einstein sorted it out it in 1905 by asking what the consequences would be for our experiences if the speed of light were the same no matter what the state of motion of the object that projects the beam is.§ He also said that there is no absolute state of motion (or absolute reference frame) to which we can compare our motion and thus no need to pose the existence of the “ether.” He showed that the major consequence of the speed of light being the same in all frames of reference is that the passage of time depends on the motion of the viewer.
To show the general idea, consider one of Einstein’s thought experiments. Suppose you were reading this book while you sat on a train moving at the speed of light away from a clock fixed on a tower. If you passed the tower precisely at twelve o’clock, what time would the clock face show 10 minutes later as you look back at the light coming from it?¶ Does that match the 12:10 showing on your wristwatch (or smartphone)? What time would it show three hours later? Not three o’clock, like on your watch? What about three days or three months later? Indeed, since you are moving at the same speed that the light is, it would never overtake you with new information. It would always read twelve o’clock.
It turns out that matter like you and the train cannot ever reach the speed of light for reasons we will show a bit later. So we have to modify the thought experiment a bit and say you are reading this book while you sit on a train moving at the 99.86% of the speed of light away from a clock fixed on a tower. If you passed the tower precisely at twelve o’clock, what time would the clock face show 10 minutes later as you look back at the light coming from it? Well, it would be slowing overtaking you and would read something like 12:03, but it would still not match the 12:10 showing on your wristwatch. The picture we develop in the next section will allow us to determine whether the clock shows 12:01 or 12:00.32 or 12:03.
We think of light as the colors red through violet in the color spectrum. But consider, why is it that you wear sunglasses that block out ultraviolet radiation? UV is a higher-energy form of light that the dyes in our eyes do not register but that will interact with (burn) our bodies. X-rays, gamma rays, and so on are even higher-energy forms of light. On the other side of the visible spectrum are the lower-energy forms of light starting with infrared, microwave, radio waves, and radar. They all travel at the same speed. The speed of light is always represented by the letter c and has been measured to be c = 186,000 miles/second.
Once we know the value of c, we can measure the distance to a spaceship by counting how many seconds pass between when we send it a radio wave and when it returns the wave to us. Likewise, when we bounce a laser beam off the Moon, we notice that there is a 1.28-second delay for each leg of the trip. That means that the distance between Earth and the Moon is
d=c t \nonumber
or
d=186,000 \text { miles } / \text { second } \times 1.28 \text { seconds }=238,000 \text { miles. } \nonumber
Note
* Your velocity of 3 m/s would add to that of the slidewalk, 3 m/s, to give 6 m/s. At this velocity, you need only 50 seconds to travel 300 m and have 10 extra seconds to casually walk onboard the plane.
† It would be 0 m/s; she would make no progress, and that is why it is fun.
‡ This term was a holdover from the Ptolemaic model of the Solar System, where ether was a substance said to fill the celestial spheres.
§ A. Einstein, Ann. Phys. (Leipzig) 17, 891 (1905); 20, 371 (1906).
¶ Twelve o’clock.
Did You Ever Wish You Had More Time?
Consider a beam of light bouncing between the mirrors of a spaceship moving, perpendicular to the light beam, at speed v relative to the ground, as seen in Figure \PageIndex{1}.
To someone sitting in the ship, the distance the beam must travel is simply the height H of the ship. The distance is the velocity c times the time of travel \tau between bounces as measured in the ship or
H=c \tau. \nonumber
Note that we use the Greek letter tau (\tau) for this time, since we know there will be two different times to consider.
To someone standing on the Earth (Figure \PageIndex{2}) the light will be seen to follow a diagonal path because the spaceship moves relative to the Earth between the time that the light is emitted near the bottom and when it is reflected from the mirror near the top of the spaceship.
Since the speed of light is the same in the Earth’s reference frame as in the reference frame of the ship, this diagonal distance is d=c \ t, where t is the time interval measured from the Earth. Finally, the ship travels a distance r = v \ t with respect to the Earth.
It is clear from Figure \PageIndex{2} that the hypotenuse d of the triangle is longer than the vertical leg H. Then since the speed of light c is the same for both the hypotenuse and the vertical leg, t must be larger than \tau. But the hypotenuse of any right triangle you can draw is always longer than each leg or is equal to the length of one leg if the length of the other is zero. (Draw several examples to prove this to yourself.) This means that t is always larger than \tau for nonzero v. We call this minimum time value \tau proper time. It is simply the time measured in any frame in which the two events are measured at the same place, such as the emission and the return points of the bouncing beam of light, or two clicks of a clock. The coordinate time interval t is measured in a frame of reference moving at velocity v relative to the frame in which the clock is stationary. (If we want to be precise, \tau in Figure \PageIndex{1} is actually half of the proper-time interval for a round trip 2 \tau. Likewise, in Figure \PageIndex{2}, t is half of the corresponding coordinate time 2 t.)
How Does This Relate to Me?
We say that the coordinate time is dilated. What exactly does that mean? It means that if your twin sister drives a fast car while you walk everywhere, she will live longer than you do—her lifetime will be dilated relative to yours! By how much?
We could find how much larger t is than \tau by using the Pythagorean theorem and some algebra* but there is a simple way to get the time-dilation factor by drawing the spaceship picture carefully, with v properly proportional to c as demonstrated in Figure \PageIndex{3}:
- Start with a square that is 10 cm on each side (the bottom side of which represents the distance light travels in the coordinate frame of reference).
- Now express the velocity of the spaceship as a fraction of the speed of light and draw a rectangle that is that same fraction of 10 cm wide and is the full 10 cm high.† Suppose v is \frac{3}{5}=\frac{6}{10} of the speed of light (111,600 miles/second); then the width of the rectangle is 6 cm, shown as red as in Figure \PageIndex{3}.
- Now trace the square onto a thin sheet of paper (or cut out a square of this size) and rotate the square around the lower left-hand corner until the lower right-hand corner of the square just touches the right-hand edge of the rectangle, approximated by the sequence of three rotated green squares shown in Figure \PageIndex{3}.
- Tape the square in place and measure the distance from the lower right-hand corner of the rotated square to the lower right-hand corner of the rectangle. For the present example, this length is 8 cm, shown as blue in Figure \PageIndex{3}. Divide 10 cm by this length to get the value of the time-dilation factor. In the present example, this ratio is \frac{5}{4} , or 1.25.
If your twin rides around in a spaceship at 111,600 miles/second for 40 years, 50 years will have passed for you when she returns! That may seem strange to you, but she is traveling at about 400 trillion miles/hour, something not exactly within your normal range of experience.
Suppose your twin slows way down, to 1/10th of the speed of light (see Figure \PageIndex{4}). Her speed is v = 0.1 c, so the width of the rectangle is 1/10 of 10 cm or 1 cm.
As you rotate the rectangle, you notice that c \ t = 10 cm is not much longer than c \ \tau = 9.95 cm. This simply shows that the dilation of coordinate time (1.01 in this case) becomes unnoticeable at velocities that are small compared to c.
So suppose your twin drives around at 70 miles/hour or 0.019 miles/second (Figure \PageIndex{5}). That is v = c/1000000 so the width of the rectangle should be 10 cm/1000000, or 80,000 times thinner than the narrowest line this printer can draw at 300 dots per inch. Even if you could draw it, you cannot see any difference between c \ t and c \ \tau, so no time dilation comes into our everyday experience.
Note
* Suppose \frac{v}{c}=\frac{3}{5} ; then the ratio of the flight path (in the Earth’s frame of reference) to the light path is also \frac{3}{5}. Let us use 3 cm and 5 cm, respectively. We can use the Pythagorean theorem to relate the two times, \tau and t:
\text { (flight path) }^{2}+(\text { vertical light path })^{2}=(\text { diagonal light path })^{2} , \nonumber
or (vertical light path)2 = (diagonal light path)2 − (flight path)2 = 25 cm2 − 9 cm2 = 16 cm2. This means that the vertical light path is 4 cm. Then t / \tau=\frac{5}{4} or 1.25.
† Suppose the speed is v = 111,600 miles/second. Then the fraction \frac{v}{c}=\frac{111600 \textit { miles } / \textit { second }}{186000 \textit { miles } / \textit { second }}=0.6. The width of the rectangle would then be 0.6 × 10 cm = 6 cm.
Relativity Bites
This is not to say that time dilation does not affect our lives. The Earth is bombarded by cosmic rays that produce showers of particles called muons in the upper atmosphere. Half of a given group of muons decays within two-millionths of a second (two microseconds) when they are at rest. That is, they have a proper half-life of two microseconds. After another two microseconds, half of those remaining decay, leaving one-fourth, and so on.
If there were no relativistic time dilation, most would decay as they travel through the depth of the atmosphere before crashing through your skull. We will show later that on average, the muons are traveling to the Earth’s surface at v = 0.9986 c. At this speed, it would take them 16 microseconds to travel through the atmosphere from the height they are produced, about 3 miles,* or about 8 half-lives.† It turns out that 18 muons are created each second over an area the width of our bodies. After 8 half-lives, \frac{1}{2^{8}} \times 18=0.07 muons per second should be left to crash through our bodies. Table \PageIndex{1} shows a progression of halving the prior number, with some rounding.
| Time | Muons left |
|---|---|
| 0 \mu s | 18 |
| 2 \mu s | 9 |
| 4 \mu s | 4 or so |
| 6 \mu s | 2 |
| 8 \mu s | 1 |
| 10 \mu s | 0.5 |
| 12 \mu s | 0.3 |
| 14 \mu s | 0.15 |
| 16 \mu s | 0.07 |
But relativity changes all this. To find the time-dilation factor for this speed, we find that we only need to rotate the square slightly to get the lower right-hand corner of the square to just touch the right-hand edge of the rectangle (see Figure \PageIndex{6}).
Note
* A. W. Wolfendale, Cosmic Rays at Ground Level (Institute of Physics, London, 1973), p. 174–75.
† t=\frac{d}{.9986 c}=\frac{3 \textit { miles }}{.9986 \times 186000 \textit { miles } / \textit { second }}=\frac{3}{1.86} \times \frac{10 \textit { seconds }}{1000000}=16 \text { microseconds. }
In this case, c \ t = 10 cm is much longer than c \ \tau = 0.52 cm. The coordinate time is extremely dilated by a factor of 19. So thanks to relativistic time dilation you measure a muon’s half-life at 19 times its proper half-life, or 38 microseconds. This is about twice the time it takes for the muons to travel through the atmosphere. That is, roughly 1/4 of them will decay, and 13 muons make it through each second* to crash through your skull and increase your cancer rate. The typical yearly dose of radiation due to these muons is 400 µsv (microsievert),† 6 times higher than a typical yearly dose of radiation due to diagnostic X-rays, 70 µsv.‡ If there were no relativistic time dilation, the yearly radiation dosage from muon exposure would be only 2 µsv. (For perspective, if I were to ask you to give me $2, the chances are pretty good you might do so. But if I asked you to give—not lend— me $400, the chances you might do so would be pretty slim.) Relativistic effects are not a minor factor in our lives at all!
Note
* National Council on Radiation Protection and Measurements, Report No. 94, Exposure of the Population in the United States and Canada from Natural Background Radiation (NCRP, Bethesda, MD, 1987), p. 12, has a rate of 0.00190 muons per cm2 per second at the surface. I obtained 13 muons per second by modeling a person by a cylinder with a radius of 15 cm.
† Alan Martin and Samuel A. Harbison, An Introduction to Radiation Protection (Chapman & Hall, New York, 1979), p. 53, gives 500 µsv for all types of cosmic radiation, of which muons make up 80%, according to the National Council on Radiation Protection and Measurements, Report No. 94, Exposure of the Population in the United States and Canada from Natural Background Radiation (NCRP, Bethesda, MD, 1987), p. 12.
‡ Alan Martin and Samuel A. Harbison, An Introduction to Radiation Protection (Chapman & Hall, New York, 1979), p. 57.
Just so that you do not get the idea that the real-world consequences of relativity are all negative, consider that evolution works by taking advantage of mutations. Theistic philosophers struggle with the question of why there are disease and evil in the world. In his last book, And God Laughed When the Birds Came Forth from the Dinosaurs, my father asked the question this way:
[W]hy does God allow such mutation, which, from the higher standpoint of the personal value that it destroys, must be classified as an “evil”? The answer that seems reasonable is to affirm that such mutation . . . is the risk God must run in creating or bringing forth a finite world of freely developing process. The over-all rationality of such possibility seems borne out by the thoughtful conclusions of genetical science itself. The geneticists Dunn and Dobzhansky write:
Harmful mutations and hereditary diseases are thus the price which the species pays for the plasticity which makes continued evolution possible.*
[T]he above quotation contains the idea of the neutrality of mutations as a necessary principle of . . . physical process. The mutation of the genes makes the survival of life possible in the long run in any environment, or amid environmental changes, within, of course, upper and lower limits of temperature and other absolute environmental boundaries for life. In theistic faith, and from the standpoint of values, this “neutrality” of mutation would itself seem purposive, since its effect is that life does survive. To theistic faith, the immanent rationale of mutation is that life shall survive.†
He also writes,
[A] modern teleological‡ view of evolution would cite mutation itself—the capacity of life at the very deepest level of process to adjust or adapt itself—as significant evidence of an ultimate spiritual meaning, design, or purpose within our world’s evolutionary development. The spiritual meaning inheres in this “free capacity,” which makes possible the manifold growth and integration of life in many experimental directions, instanced by all the past and present organic forms.§
Note
* L. C. Dunn and Th. Dobzhansky, Heredity, Race, and Society, A Mentor Book (New American Library, New York, 1946/1952), p. 81.
† G. Douglas Straton, And God Laughed When the Birds Came Forth from the Dinosaurs: Essays on the Idea and Knowledge of God (1995 ms.), Chap. 6, p. 163.
‡ Teleology is the study of cosmic design
§ G. Douglas Straton, And God Laughed When the Birds Came Forth from the Dinosaurs: Essays on the Idea and Knowledge of God (1995 ms.), Chap. 5, p. 115.
Clearly, if relativity were not working, evolution would have proceeded at a pace that is between 5 and 256 times slower (28).† The Earth would have had to wait 18 to 900 billion years for intelligent life to form (instead of 3.5 billion years)—much longer than the Sun’s 10-billion-year lifetime!
Put another way, the person attempting to write this book today would likely be a mess of green slime had relativity not offered us its gifts.
There Are Cops, You Know!
What about people traveling at super high speeds, such as v = 0.9986 c in Figure \PageIndex{6}? Suppose your twin left Earth when you were 20 years of age, traveled for 10 years at v = 0.9986 c, and then returned to Earth to tell you about her trip. Tough luck; you would have died of old age a century before she returned! You were both 20 when she left. She is 30 years old (20 + 10) when she returns (both her clock and her body agree with this assertion), but you would be 210 years old (20 + 10 × 19) had you lived.
As we increase the speed from this point, we will find that we reach a limit in our ability to graph. But this limit expresses a reality of nature. As the velocity v of a rocket approaches that of the speed of light c, the right-hand side of the rectangle really does approach the right side of the 10 cm square in Figure \PageIndex{6}. The limit as v goes to c is that the rectangle goes to a square. Then we have to move the square not at all to get its lower right-hand corner to touch the right side of the rectangle-which-is-a-square. That is, c \tau = 0 cm.
A finite coordinate time period in a rocket moving at velocity v = c relative to the Earth corresponds to zero proper time. What does that mean? If we divide 10 cm by 0 cm we get an infinite time-dilation factor.‡
We actually never run into this infinite limit because it is impossible to exert sufficient force on the rocket to get it moving at the speed c. The reason is that whatever force is exerted on the rocket to increase its velocity is spread out over a longer and longer period of Earth coordinate time as v approaches c. We would have to wait an infinite amount of Earth coordinate time to see the rocket reach the speed of light.
Note
† The maximal value is assuming that the other 100 µsv of cosmic radiation noted in Alan Martin and Samuel A. Harbison’s An Introduction to Radiation Protection (Chapman & Hall, New York, 1979), p. 53, would have a similar reduction in the absence of relativity; the minimal value assumes that there would be no such reduction.
‡ To see this consider the following pattern: On your calculator divide 10 by 10 to get 1; 10/1 = 10; 10/0.1 = 100; 10/0.01 = 1,000; 10/0.001 = 10,000; 10/0.0001 = 100,000; 10/0.00001 = 1,000,000; and so on. As you divide 10 by smaller and smaller numbers, you get a result that is bigger and bigger. Infinity is the limit of this sequence.
To see how this works, imagine a spaceship powered by small nuclear bombs that are dropped through a small hole in a radiation shield attached to the passenger cabin. When a bomb explodes, half of the exploded material and associated photons push against the radiation shield, shoving the rocket faster in its direction of travel. As the rocket’s velocity increases, the time dilation increases on Earth, which the passengers have left behind. As the rocket crew steadily drops and explodes bombs (at a steady proper-time interval), there are longer and longer time intervals between when Earth folk see the photons from the explosions arrive. In fact, as the people on Earth see the rocket’s speed approach the speed of light, they have to wait through an infinite time interval for the explosion that would have just pushed the rocket past the limit. Thus, the rocket never reaches the speed of light relative to the Earth. One might rephrase the classic Western koan as “What happens when an irresistible force meets an interminable stasis?”
Some readers will note that many science popularizers and introductory physics teachers used to invoke the idea that
[t]he faster a particle is pushed, the more its mass increases, thereby resulting in less and less response to the accelerating force. . . . [A]s v approaches c, m approaches infinity! [To push a particle] to the speed of light . . . would require an infinite force, which is clearly impossible.*
Let me caution you that research physicists rely heavily upon the fact† that the mass of a particle is the same in all frames of references; it is an invariant quantity.‡
See, for instance, the caption of Figure \PageIndex{4} in the paper publishing the discovery of the Higgs boson,§ reproduced below, that begins with the explicit acknowledgment of the “[i]nvariant mass distribution,” while the simpler and equivalent “mass” is also used throughout, such as in the section G, following that figure: “The measured Higgs boson mass [is] 125.98 ± 0.50 GeV. . . .” The (invariant) mass of an object is sometimes referred to in older texts as the “rest mass.”
Note
* Paul G. Hewitt, Conceptual Physics, 6th ed. (Scott, Foresman & Co., Boston, 1989), p. 662.
† For a complete history of this, see Lev. B. Okun, Phys. Today 42, 31–36 (June 1989).
‡ See, for instance, the standard textbook by John D. Jackson, Classical Electrodynamics (John Wiley & Sons, New York, 1975), p. 531, eq. (11.54).
§ G. Aad et al. (ATLAS Collaboration), Phys. Rev. D 90, 052004 (2014).
Figure \PageIndex{7}: Invariant mass distribution in the H → \gamma \gamma analysis for data (7 TeV and 8 TeV samples combined), showing weighted data points with errors, and the result of the simultaneous fit to all categories. The fitted signal plus background is shown, along with the background-only component of this fit. The different categories are summed together with a weight given by the s/b ratio in each category. The bottom plot shows the difference between the summed weights and the background component of the fit.
Figure 4 of G. Aad et al. (ATLAS Collaboration), Phys. Rev. D 90, 052004, reproduced under the terms of the Creative Commons Attribution 3.0 License.
The idea that mass increases with velocity was introduced by Hendrick Lorentz* in 1899 so that he could use the low-speed expression for momentum, m v, for relativistically high velocities. When Einstein introduced relativity six years later, the idea of mass increasing with velocity became unnecessary, but unfortunately, it has retained a very long life. This puts you, the reader, in the nasty position of having to decide between two “authorities.” Since the explanation for the upper limit on rocket speeds given on the previous page does not need to mention mass, changing or otherwise, Occam’s razor† would dictate that we choose it over an explanation that includes the idea of varying mass. I would recommend that you discard the latter idea as outdated. After all, the downside of using a convenient, though incorrect, model to make predictions is revealed well in the story of the Ptolemaic vs. Copernican models of the Solar System.
A Short Tale
So everything you believe about time has just gotten blown out the window. About now, I would expect you to be wondering if space gets messed with too. It does.
Unfortunately, the pictures below show this only with the aid of a series of length comparisons. In my experience, those who are a bit wigged out by math may put up with a single such relation here and there, but a series of about eight length comparisons that build up to the answer may well lead to frustration. So let me simply give you the result here and you can just skim over the notes below as if they were written in Portuguese, from which a recognizable word or two might pop out if you know a bit of Spanish or French. If you would like to bypass the comparisons entirely, read the following paragraph and then just jump to the words Skip to here.
The length \ell of the rocket measured by Earth is contracted by the same factor, relative to the proper length L, as the time t measured by Earth is dilated relative to proper time \tau. Since we keep on finding this “factor,” we had better give it a name. It is always represented by the Greek letter for g, gamma, which is written \gamma. That is, t=\gamma \ \tau, and \ell=\frac{L}{\gamma}.
Here are the details. Consider our spaceship at rest, with an additional pair of mirrors set at the same distance horizontally as the original ones were set vertically (see Figure \PageIndex{8}. Then if a light wave is emitted from the lower left-hand corner of the set of mirrors, it will travel outward in concentric rings, strike the top and right-hand mirrors simultaneously, and be reflected back to the emission point. The total distance traveled in this proper-time interval is
2 L=c \tau. \nonumber
Now suppose the rocket is moving at velocity v=\frac{3}{5} c relative to the Earth. If the spaceship were at rest, light emitted from the left-hand mirror would have to travel a distance \ell to the right-hand mirror in Figure \PageIndex{9a}. But in time t_{a}, that right-hand mirror moves with the spaceship an additional distance, a=v \ t_{a}, before the light catches up (Figure \PageIndex{9c}). So the distance that light must move in that same time is
c \ t_{a}=\ell+v \ t_{a}. \nonumber
Subtracting v \ t_{a} from both sides, collecting terms, and using v=\frac{3}{5} c gives
\begin{array}{l} c t_{a}-v t_{a}=c t_{a}\left(1-\frac{v}{c}\right) \\ =c t_{a}\left(1-\frac{3}{5}\right)=\ell \ , \end{array} \nonumber
or
c t_{a}=\frac{5}{2} \ell. \nonumber
In this time, the rocket travels 3/5 as far as the light,
a=v t_{a}=\frac{3}{5} c t_{a}=\frac{3}{2} \ell. \nonumber
A much shorter time later, t_{b} , the reflected wave collides with the bottom left-hand mirror, traveling toward it rather than away this time (Figure \PageIndex{9d}), so that
\begin{array}{c} c t_{b}=\ell-v t_{b}, \text { or } \\ c t_{b}+v t_{b}=c t_{b}\left(1+\frac{v}{c}\right) \\ =c t_{b}\left(1+\frac{3}{5}\right)=\ell \ , \end{array} \nonumber
and (multiplying both sides by \frac{5}{8} )
c t_{b}=\frac{5}{8} \ell, \nonumber
3/5 of which is
b=v t_{b}=\frac{3}{8} \ell, \nonumber
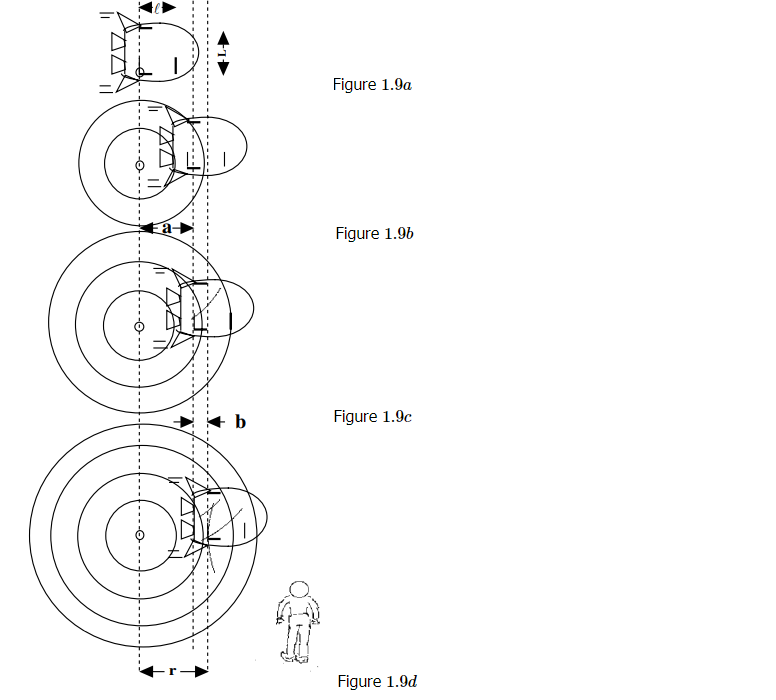
Figure \PageIndex{9}
(CC BY-NC-ND; Jack C. Straton)
Then the total distance the rocket travels for the emission and reflection is the sum of these, r=v t=a+b=\frac{3}{2} \times \frac{4}{4} \ell+\frac{3}{8} \ell=\mathbf{3 \times} \frac{5 \ell}{8}, which is again \frac{3}{5} of the distance the light travels in the same time, c t=\frac{5}{2} \times \frac{4}{4} \ell+\frac{5}{8} \ell=5 \times \frac{5 \ell}{8}. We found from our time-dilation calculation in Figure \PageIndex{2} that if one leg is 3 units long when the hypotenuse is 5 units long, then the other leg has to be 4 units long. This is the case in the two expressions above for the leg and hypotenuse, where the unit of measure is \frac{5 \ell}{8}. So c \tau=4 \times \frac{5 \ell}{8}.
But from Figure \PageIndex{8}, we see that c \ \tau=2 L. Comparing these two expressions shows that
\ell=\frac{8}{5} \times \frac{2 L}{4}=\frac{4}{5} L. \nonumber
(Skip to here.) Comparing this to the time-dilation expression we obtained from Figure \PageIndex{3}, t=\frac{5}{4} \tau shows that the length \ell of the rocket measured by Earth is contracted, relative to the proper length L, by the same factor \gamma=\frac{5}{4}, as the time t measured by Earth is dilated relative to proper time \tau. That is t=\gamma \tau and \ell=\frac{L}{\gamma}.
This compensation between time dilation and length contraction is necessary for reality to be whole. Einstein’s second postulate of relativity was that no experiment you could perform would tell you whether it was your frame of reference that was moving or someone else’s (alternatively stated, motion is relative, or there is no preferred frame of reference).
Consider our example of the time dilation of muons created in the Earth’s atmosphere. These muons are free to think they are at rest and it is the Earth that is moving toward them. They see the surface of the Earth traveling toward them at v = 0.9986 c just after they are produced.
At this speed, it would take the Earth’s 3 miles of atmosphere 16 microseconds to pass by them before the surface crashes into them. As before, this is about 8 proper half-lives. If there were no relativistic length contraction, most would decay before they saw your head approaching as you stood on the surface of the Earth. But because of relativity, the muons see the Earth’s atmosphere contracted to only 1/6 of a mile.* The time it takes the Earth’s surface to hit them is then 0.8 microseconds, or about half of the muon half-life.† Again, we get the result that roughly 1/4 of the muons decay, leaving 13 muons getting hit by your head each second before their lives are over. Without length contraction, the physical reality of your cancer risk would depend on which frame of reference does the calculation. That would violate Einstein’s principle of relativity.


