5.1: What is Inertial Motion?

Learning Objectives

• Explain the inertial motion

In section 2.3, I stated the following as an axiom of special relativity:

P4: Inertial frames of reference exist. These are frames in which particles move at constant velocity if not subject to any forces. We can construct such a frame by using a particular particle, which is not subject to any forces, as a reference point. Inertial motion is modeled by vectors and parallelism.

This is a typical modern restatement of Newton’s first law. It claims to define inertial frames and claims that they exist.

An operational definition

Figure \(\PageIndex{1}\): The spherical chamber, shown in a cutaway view, has layers of shielding to exclude all known nongravitational forces. The three guns, at right angles to each other, fire bullets. Once the chamber has been calibrated by marking the three dashed-line trajectories under free-fall conditions, an observer inside the chamber can always tell whether she is in a ninertial frame.

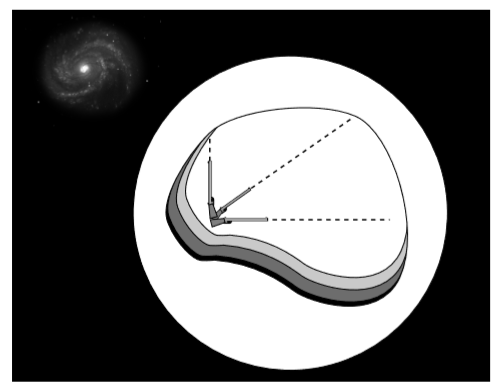
In keeping with the philosophy of operationalism, we ought to be able to translate the definition into a method for testing whether a given frame really is inertial. Figure \(\PageIndex{1}\) shows an idealized variation on a device actually built for this purpose by Harold Waage at Princeton as a lecture demonstration to be used by his partner in crime John Wheeler. We build a sealed chamber whose contents are isolated as much as possible from outside forces. Of the four known forces of nature, the ones we know how to exclude are the strong nuclear force, the weak nuclear force, and the electromagnetic force. The strong nuclear force has a range of only about \(1\: fm\) (\(10^{-15} m\)), so to exclude it we merely need to make the chamber thicker than that, and also surround it with enough paraffin wax to keep out any neutrons that happen to be flying by. The weak nuclear force also has a short range, and although shielding against neutrinos is a practical impossibility, their influence on the apparatus inside will be negligible. To shield against electromagnetic forces, we surround the chamber with a Faraday cage and a solid sheet of mu-metal. Finally, we make sure that the chamber is not being touched by any surrounding matter, so that short-range residual electrical forces (sticky forces, chemical bonds, etc.) are excluded. That is, the chamber cannot be supported; it is free-falling.

Crucially, the shielding does not exclude gravitational forces. There is in fact no known way of shielding against gravitational effects such as the attraction of other masses or the propagation of gravitational waves. (Because the shielding is spherical, it exerts no gravitational force of its own on the apparatus inside.)

Inside, an observer carries out an initial calibration by firing bullets along three Cartesian axes and tracing their paths, which she defines to be linear. (She can also make sure that the chamber isn’t rotating, e.g., by checking for velocity-dependent Coriolis forces.) After the initial calibration, she can always tell whether or not she is in an inertial frame. She simply has to fire the bullets, and see whether or not they follow the precalibrated paths. For example, she can detect that the frame has become noninertial if the chamber is rotated, allowed to rest on the ground, or accelerated by a rocket engine.

Isaac Newton would have been extremely unhappy with our definition. “This is absurd,” he says. “The way you’ve defined it, my street in London isn’t inertial.” Newtonian mechanics only makes predictions if we input the correct data on all the mass in the universe. Given this kind of knowledge, we can properly account for all the gravitational forces, and define the street in London as an inertial frame because in that frame, the trees and houses have zero total force on them and don’t accelerate. But spacetime isn’t Galilean. In special relativity’s description of spacetime, information propagates at a maximum speed of \(c\), so there will always be distant parts of the universe that we can never know about, because information from those regions hasn’t had time to reach us yet.

Example \(\PageIndex{1}\): Rotation is noninertial

Figure \(\PageIndex{2}\) shows a hypothetical example proposed by Einstein. One planet rotates about its axis and therefore has an equatorial bulge. The other planet doesn’t rotate and has none. Both Newtonian mechanics and special relativity make these predictions, and although the scenario is idealized and unrealistic, there is no doubt that their predictions are correct for this situation, because the two theories have been tested in similar cases. This also agrees with our operational definition of inertial motion as stated above. Rotational motion is noninertial.

Figure \(\PageIndex{2}\): Hypothetical example proposed by Einstein

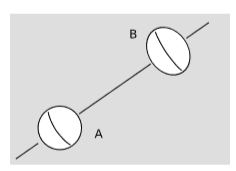
This bothered Einstein for the following reason. If the inhabitants of the two planets can look up in the sky at the “fixed stars,” they have a clear explanation of the reason for the difference in shape. People on planet A don’t see the stars rise or set, and they infer that this is because they live on a nonrotating world. The inhabitants of planet B do see the stars rise and set, just as they do here on earth, so they infer, just as Copernicus did, that their planet rotates.

But suppose, Einstein said, that the two planets exist alone in an otherwise empty universe. There are no stars. Then it’s equally valid for someone on either planet to say that it’s the one that doesn’t rotate. Each planet rotates relative to the other planet, but the situation now appears completely symmetric. Einstein took this argument seriously and felt that it showed a defect in special relativity. He hoped that his theory of general relativity would fix this problem, and predict that in another wise empty universe, neither planet would show any tidal bulge. In reality,further study of the general theory of relativity showed that it made the same prediction as special relativity. Theorists have constructed other theories of gravity, most prominently the Brans-Dicke theory, that do behave more in the way Einstein’s physical intuition expected. Precise solar-system tests have, however, supported general relativity rather than Brans-Dicke gravity, so it appears well settled now that rotational motion really shouldn’t be considered inertial.

Equivalence of Inertial and Gravitational Mass

All of the reasoning above depends on the perfect cancellation referred to by Newton: since gravitational forces are proportional to mass, and acceleration is inversely proportional to mass, the result is that accelerations caused by gravity are independent of mass. This is the universality of free fall, which was famously observed by Galileo, Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): According to Galileo’s student Viviani, Galileo dropped a cannonball and a musketball simultaneously from the leaning tower of Pisa, and observed that they hit the ground at nearly the same time. This contradicted Aristotle’s long-accepted idea that heavier objects fell faster.

Suppose that, on the contrary, we had access to some matter that was immune to gravity. It’s sold under the brand name FloatyStuff^TM. The cancellation fails now. Let’s say that alien gangsters land in a flying saucer, kidnap you out of your back yard, konk you on the head, and take you away. When you regain consciousness, you’re locked up in a sealed cabin in their spaceship. You pull your keychain out of your pocket and release it, and you observe that it accelerates toward the floor with an acceleration that seems quite a bit slower than what you’re used to on earth, perhaps a third of a gee. There are two possible explanations for this. One is that the aliens have taken you to some other planet, maybe Mars, where the strength of gravity is a third of what we have on earth. The other is that your keychain didn’t really accelerate at all: you’re still inside the flying saucer, which is accelerating at a third of a gee, so that it was really the deck that accelerated up and hit the keys.

There is absolutely no way to tell which of these two scenarios is actually the case — unless you happen to have a chunk of FloatyStuff in your other pocket. If you release the FloatyStuff and it hovers above the deck, then you’re on another planet and experiencing genuine gravity; your keychain responded to the gravity, but the FloatyStuff didn’t. But if you release the FloatyStuff and see it hit the deck, then the flying saucer is accelerating through outer space.