5.2: The Equivalence Principle

Learning Objectives

• Explain the Equivalence Principle

Equivalence of acceleration to a gravitational field

The nonexistence of FloatyStuff in our universe is a special case of the equivalence principle. The equivalence principle states that an acceleration (such as the acceleration of the flying saucer) is always equivalent to a gravitational field, and no observation can ever tell the difference without reference to something external. (And suppose you did have some external reference point — how would you know whether it was accelerating?)

Eötvös experiments

FloatyStuff would be an extreme example, but if there was any violation of the universality of free fall, no matter how small, then the equivalence principle would be falsified. Since Galileo’s time, experimental methods have had several centuries in which to improve, and the second law has been subjected to similar tests with exponentially improving precision. For such an experiment in 1993,¹ physicists at the University of Pisa (!) built a metal disk out of copper and tungsten semicircles joined together at their flat edges. They evacuated the air from a vertical shaft and dropped the disk down it \(142\) times, using lasers to measure any tiny rotation that would result if the accelerations of the copper and tungsten were very slightly different. The results were statistically consistent with zero rotation, and put an upper limit of \(1×10^{-9}\) on the fractional difference in acceleration

\[\frac{ |g_{copper} - g_{tungsten}|}{g}\]

Experiments of this type are called Eötvös experiments, after Loránd Eötvös, who did the first modern, high-precision versions.

Figure \(\PageIndex{1}\): Loránd Eötvös (1848-1919).

Example \(\PageIndex{1}\): The artificial horizon

Figure \(\PageIndex{2}\): An artificial horizon.

The pilot of an airplane cannot always easily tell which way is up. The horizon may not be level simply because the ground has an actual slope, and in any case the horizon may not be visible if the weather is foggy. One might imagine that the problem could be solved simply by hanging a pendulum and observing which way it pointed, but by the equivalence principle the pendulum cannot tell the difference between a gravitational field and an acceleration of the aircraft relative to the ground — nor can any other accelerometer, such as the pilot’s inner ear. For example, when the plane is turning to the right, accelerometers will be tricked into believing that “down” is down and to the left. To get around this problem, airplanes use a device called an artificial horizon, which is essentially a gyroscope. The gyroscope has to be initialized when the plane is known to be oriented in a horizontal plane. No gyroscope is perfect, so over time it will drift. For this reason the instrument also contains an accelerometer, and the gyroscope is automatically restored to agreement with the accelerometer, with a time-constant of several minutes. If the plane is flown in circles for several minutes, the artificial horizon will be fooled into indicating that the wrong direction is vertical.

Gravity without gravity

We live immersed in the earth’s gravitational field, and that is where we do almost all of our physics experiments. It’s surprising, then, that special relativity can be confirmed in earthbound experiments, sometimes with phenomonal precision, as in the Ives-Stilwell experiment’s \(10\)-significant-figure test of the relativistic Doppler shift equation. How can this be, since special relativity is supposed to be the version of relativity that can’t handle gravity? The equivalence principle provides an answer. If the only gravitational effect on your experiment is a uniform field \(g\), then it’s valid for you to describe your experiment as having been done in a region without any gravity, but in a laboratory whose floor happened to have been accelerating upward with an acceleration \(-g\). Special relativity works just fine in such situations, because switching into an accelerated frame of reference doesn’t have any effect on the flatness of spacetime. Note that Gravity Probe B orbited the earth, so the field it experienced varied in direction, causing the above argument to fail; the effects it observed were not explainable by special relativity.

Gravitational Doppler shifts

Figure \(\PageIndex{3}\): 1. A light wave is emitted upward from the floor of the elevator. The elevator accelerates upward. 2. By the time the light wave is detected at the ceiling, the elevator has changed its velocity, so the wave is detected with a Doppler shift.

For an example of a specifically gravitational experiment that is explainable by special relativity, and that has actually been carried out, In a laboratory accelerating upward, a light wave emitted from the floor would be Doppler-shifted toward lower frequencies when observed at the ceiling, because of the change in the receiver’s velocity during the wave’s time of flight. The effect is given by

\[\frac{\Delta f}{f} \approx \frac{-a\Delta x}{c^2}\]

where a is the lab’s acceleration, \(∆x\) is the height from floor to ceiling, and \(c\) is the speed of light.

In units with \(c = 1\), we have

\[\frac{\Delta f}{f} \approx -a\Delta x\]

By the equivalence principle, we find that when such an experiment is done in a gravitational field \(g\), there should be a gravitational effect on frequency

\[\frac{\Delta f}{f} \approx -g\Delta x\]

This can be expressed more compactly as

\[\frac{\Delta f}{f} \approx -\Delta \Phi\]

where \(Φ\) is the gravitational potential, i.e., the gravitational energy per unit mass.

Figure \(\PageIndex{4}\): Pound and Rebka at the top and bottom of the tower.

In 1959, Pound and Rebka² carried out an experiment in a tower at Harvard. Gamma rays from were emitted by a \(^{57}\textrm{Fe}\) source at the bottom and detected at the top, having risen \(∆x = 22.6 m\). The equivalence principle predicts a fractional frequency shift due to gravity of \(2.46×10^{-15}\). This is very small, and would normally have been masked by recoil effects, but by exploiting the Mössbauer effect Pound and Rebka measured the shift to be \((2.56±0.25)×10^{-15}\).

A varying metric

In the Pound-Rebka experiment, the nuclei emitting the gamma rays at frequency \(f\) can be thought of as little clocks. Each wave crest that propagates upward is a signal saying that the clock has ticked once. An observer at the top of the tower finds that the signals come in at the lower frequency \(f'\), and concludes naturally that the clocks at the bottom had been slowed down due to some kind of time dilation effect arising from gravity.

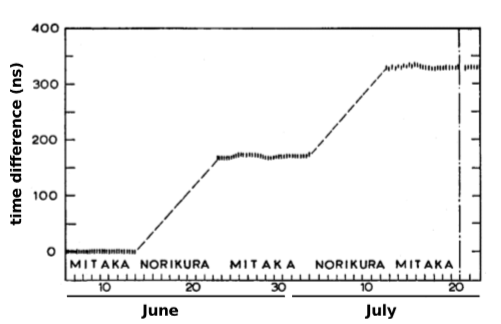
This may seem like a big conceptual leap, but it has been confirmed using atomic clocks. In a 1978 experiment by Iijima and Fujiwara, figure \(\PageIndex{5}\), identical atomic clocks were kept at rest at the top and bottom of a mountain near Tokyo. The discrepancies between the clocks were consistent with the predictions of the equivalence principle. The gravitational Doppler shift was also one of the effects that led to the non-null result of the Hafele-Keating experiment, in which atomic clocks were flown around the world aboard commercial passenger jets. Every time you use the GPS system, you are making use of these effects.

Figure \(\PageIndex{5}\): A graph showing the time difference between two atomic clocks. One clock was kept at Mitaka Observatory, at 58 m above sea level. The other was moved back and forth to a second observatory, Norikura Corona Station, at the peak of the Norikura volcano, 2876 m above sea level. The plateaus on the graph are data from the periods when the clocks were compared side by side at Mitaka. The difference between one plateau and the next shows a gravitational effect on the rate of flow of time, accumulated during the period when the mobile clock was at the top of Norikura.

Starting from only the seemingly innocuous assumption of the equivalence principle, we are led to surprisingly far-reaching conclusions. We find that time flows at different rates depending on the height within a gravitational field. Since the metric can be interpreted as a measure of the amount of proper time along a given world-line, we conclude that we cannot always express the metric in the familiar form \(\tau ^2 = (+1)\Delta t^2 + (-1)\Delta x^2\) with fixed coefficients \(+1\) and \(-1\). Suppose that the \(t\) coordinate is defined by radio synchronization. Then the \(+1\) in the metric needs to be replaced with approximately \(1 + 2Φ\), where we take \(Φ = 0\) by convention at the height of the standard clock that coordinates the synchronization.

Keep in mind that although we have connected gravity to the measurement apparatus of special relativity, there is no curvature of spacetime, so what we are doing here is still special relativity, not general relativity. In fact there is nothing more mysterious going on here than a renaming of spacetime events through a change of coordinates. The renaming might be convenient if we were using earth-based reference points to measure the \(x\) coordinate. But if we felt like it, we could switch to a good inertial frame of reference, one that was free-falling. In this frame, we would obtain exactly the same prediction for the results of any experiment. For example, the free-falling observer would explain the result of the Pound-Rebka experiment as arising from the upward acceleration of the detector away from the source.

References

¹ Carusotto et al., “Limits on the violation of g-universality with a Galileotype experiment,” Phys Lett A183 (1993) 355. Freely available online at researchgate.net.

² Phys. Rev. Lett. 4 (1960) 337