14: The Clausius-Clapeyron Equation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Before starting this chapter, it would probably be a good idea to re-read Sections 9.2 and 9.3 of Chapter 9.
The Clausius-Clapeyron equation relates the latent heat (heat of transformation) of vaporization or condensation to the rate of change of vapour pressure with temperature. Or, in the case of a solid-liquid transformation, it relates the latent heat of fusion or solidification to the rate of change of melting point with pressure.
Let us imagine a vapour in equilibrium with its liquid held in a cylinder by a piston, at a constant temperature – namely the temperature at which the liquid and vapour are in equilibrium − that is to say, the boiling (or condensation) point for that pressure. We imagine the piston to be pulled out, at constant temperature; liquid evaporates and the pressure remains constant. If the piston is pushed in, vapour condenses, at constant temperature and pressure. During this process the pressure and temperature remain constant, so the Gibbs free energy of the system is constant.
Let G1 be the specific Gibbs free energy for the liquid
and G2 be the specific Gibbs free energy for the vapour.
Suppose that a mass dm of the liquid vaporizes, so that the Gibbs free energy for the liquid decreases by G1dm and the Gibbs free energy for the vapour increases by G2dm. But the Gibbs free energy for the system is constant. This therefore shows that, when we have a liquid in equilibrium with its vapour (i.e. at its boiling point) the specific Gibbs free energies of liquid and vapour are equal. (The same is true, of course, for the molar Gibbs free energies.) That is:
H1−TS1=H2−TS2
or
T(S2−S1)=H2−H1,
in which the enthalpy and entropy are specific. The left hand side is the specific latent heat of vaporization, and we already knew from Chapter 9 that this was equal to the difference in the specific enthalpies of liquid and vapour.
The equality of the specific Gibbs free energies of liquid and vapour can also be written
U1−TS1+PV1=U2−TS2+PV2,
or
T(S2−S1)=(U2−U1)+P(V2−V1).
This shows that the latent heat of vaporization goes into two things: To increase the internal energy upon vaporization (especially the increase of potential energy as the molecules are pulled apart from each other) and the PdV work done against the external pressure as the volume increases. Thus we could divide the latent heat into an internal latent heat and an external latent heat.
In the foregoing, we imagined that some liquid vaporized as we withdrew the piston. Now let us imagine that we cause some liquid to vaporize as we add some heat at constant volume. The specific Gibbs free energies of liquid and vapour both increase, but they increase by the same amount because, as we have seen, when a liquid and its vapour are in equilibrium at the boiling point, their specific Gibbs free energies are equal. Thus
−S1dT+V1dP=−S2dT+V2dP,
or
dPdT=S2−S1V2−V1.
The left hand side is the rate of increase of vapour pressure with temperature, while S2 − S1 is equal to L/T, where L is the specific latent heat of vaporization. Thus we arrive at the Clausius-Clapeyron equation:
dPdT=LT(V2−VL).
Example: At 100 oC the rate of increase of vapour pressure of steam is 27.1 mm Hg per Celsius degree, and a gram of steam occupies 1674 cm3. What is the specific latent heat of vaporization?
Answer: L=T(V2−V1)dPdT.
T=373.15K.V2−V1=1.673m3kg−1.
dPdT=1.36×104×9.81×2.71×10−2=3.616PaK−1.
Hence
L=2.26×106Jkg−1__.
The same argument can be used to relate the rate of change of melting point with pressure of a solid with its latent heat of fusion. The Clausius-Clapeyron equation then takes the form
dTdP=T(V2−V1)L.
For most substances, the specific volume of the liquid (V2) is greater than the specific volume of the solid (V1); but for H2O, Bi and Ga, V2 < V1 and dT/dP is negative.
Example: For the ice-water system,
L=3.36×105Jkg−1V2=10−3m3kg−1V1=1.091×10−3m3kg−1T=273.15K
Hence
dTdP=−7.4×10−8KPa−1
That’s about −7.4 × 10−3 kelvins per atmosphere
Solids, Liquids, Gases, Entropy and the Gibbs Function.
Of the three phases, solid, liquid and vapour, solid is the most ordered (has the least entropy) and vapour is the most disordered (has the most entropy). Now equation 12.6.12a tells us that (∂G/∂T) = −S. This means that, at a given pressure, the Gibbs function of the vapour decreases rapidly with increasing temperature, whereas the Gibbs function of a solid decreases relatively slowly. Schematically the Gibbs function of the three phases for H2O at atmospheric pressure looks something like this:
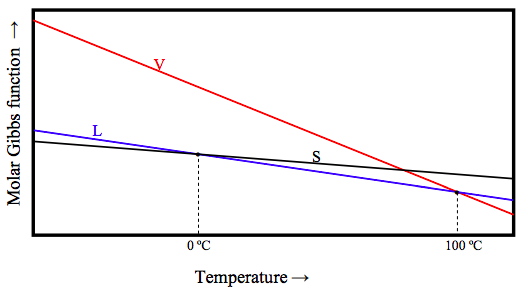
Below 0 ºC, the Gibbs function is lowest for the solid, and that is the stable phase. Between 0 ºC and 100 ºC, the Gibbs function is lowest for the liquid, and that is the stable phase. Above 100 ºC, the Gibbs function is lowest for the vapour, and that is the stable phase. At 0 ºC, the molar Gibbs function of solid and liquid are equal; the two phases there are in equilibrium. At 100 ºC, the molar Gibbs function of gas and liquid are equal; the two phases there are in equilibrium.
The slopes and intercepts of these lines vary not only from substance to substance, but also, for a given substance, with pressure. The Maxwell relation 12.6.16, (∂S∂P)T=−(∂V∂T)P, tells us that the manner in which entropy changes with pressure is related to the expansion coefficient. For most substances (water between 0 ºC and 4 ºC is an exception), the coefficient of expansion is positive, so this tells us that entropy decreases with increasing pressure, and increases with decreasing pressure. The change in entropy with pressure is greatest for the vapour, so that, at lower pressures the slope of the vapour line in the graph of Gibbs function with temperature will be much steeper, and the situation will look like this:
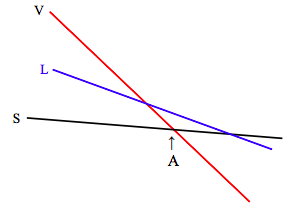
At temperatures below A, the Gibbs function is lowest for the solid, and that is the stable phase. At temperature above A, the Gibbs function is lowest for the vapour, and that is the stable phase. At the pressure represented in the above diagram, the liquid is never the stable phase. The substance sublimates from solid to vapour as the temperature is raised.
At the pressure corresponding to the triple point line (remind yourself by looking at figures VI.3, VI.4 and VI.8), the diagram looks like:
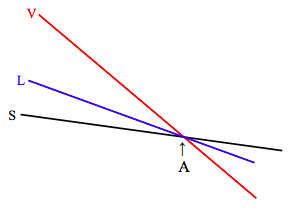
At the triple point (A) the molar Gibbs functions of all three phases are equal, and all three phases are in equilibrium. As you increase the temperature from below A to above A, the substance sublimates directly from solid to vapour, as can also be seen from figure VI.5.


