2.4: The First Law of Thermodynamics

\( \newcommand\bes{\begin{equation}\begin{split}}\)
\( \newcommand\ltwid{\propto}\)
\( \newcommand\ees{\end{split}\end{equation}}\)
\( \newcommand\mib{\mathbf}\)
\( \newcommand\Sa{\textsf a}\)
\( \newcommand\Sb{\textsf b}\)
\( \newcommand\Sc{\textsf c}\)
\( \newcommand\Sd{\textsf d}\)
\( \newcommand\Se{\textsf e}\)
\( \newcommand\Sf{\textsf f}\)
\( \newcommand\Sg{\textsf g}\)
\( \newcommand\Sh{\textsf h}\)
\( \newcommand\Si{\textsf i}\)
\( \newcommand\Sj{\textsf j}\)
\( \newcommand\Sk{\textsf k}\)
\( \newcommand\Sl{\textsf l}\)
\( \newcommand\Sm{\textsf m}\)
\( \newcommand\Sn{\textsf n}\)
\( \newcommand\So{\textsf o}\)
\( \newcommand\Sp{\textsf p}\)
\( \newcommand\Sq{\textsf q}\)
\( \newcommand\Sr{\textsf r}\)
\( \newcommand\Ss{\textsf s}\)
\( \newcommand\St{\textsf t}\)
\( \newcommand\Su{\textsf u}\)
\( \newcommand\Sv{\textsf v}\)
\( \newcommand\Sw{\textsf w}\)
\( \newcommand\Sx{\textsf x}\)
\( \newcommand\Sy{\textsf y}\)
\( \newcommand\Sz{\textsf z}\)
\( \newcommand\SA{\textsf A}\)
\( \newcommand\SB{\textsf B}\)
\( \newcommand\SC{\textsf C}\)
\( \newcommand\SD{\textsf D}\)
\( \newcommand\SE{\textsf E}\)
\( \newcommand\SF{\textsf F}\)
\( \newcommand\SG{\textsf G}\)
\( \newcommand\SH{\textsf H}\)
\( \newcommand\SI{\textsf I}\)
\( \newcommand\SJ{\textsf J}\)
\( \newcommand\SK{\textsf K}\)
\( \newcommand\SL{\textsf L}\)
\( \newcommand\SM{\textsf M}\)
\( \newcommand\SN{\textsf N}\)
\( \newcommand\SO{\textsf O}\)
\( \newcommand\SP{\textsf P}\)
\( \newcommand\SQ{\textsf Q}\)
\( \newcommand\SR{\textsf R}\)
\( \newcommand\SS{\textsf S}\)
\( \newcommand\ST{\textsf T}\)
\( \newcommand\SU{\textsf U}\)
\( \newcommand\SV{\textsf V}\)
\( \newcommand\SW{\textsf W}\)
\( \newcommand\SX{\textsf X}\)
\( \newcommand\SY{\textsf Y}\)
\( \newcommand\SZ{\textsf Z}\)
\( \newcommand\Ha{\hat a}\)
\( \newcommand\Hb{\hat b}\)
\( \newcommand\Hc{\hat c}\)
\( \newcommand\Hd{\hat d}\)
\( \newcommand\He{\hat e}\)
\( \newcommand\Hf{\hat f}\)
\( \newcommand\Hg{\hat g}\)
\( \newcommand\Hh{\hat h}\)
\( \newcommand\Hi{\hat \imath}\)
\( \newcommand\Hj{\hat \jmath}\)
\( \newcommand\Hk{\hat k}\)
\( \newcommand\Hl{\hat l}\)
\( \newcommand\Hm{\hat m}\)
\( \newcommand\Hn{\hat n}\)
\( \newcommand\Ho{\hat o}\)
\( \newcommand\Hp{\hat p}\)
\( \newcommand\Hq{\hat q}\)
\( \newcommand\Hr{\hat r}\)
\( \newcommand\Hs{\hat s}\)
\( \newcommand\Ht{\hat t}\)
\( \newcommand\Hu{\hat u}\)
\( \newcommand\Hv{\hat v}\)
\( \newcommand\Hw{\hat w}\)
\( \newcommand\Hx{\hat x}\)
\( \newcommand\Hy{\hat y}\)
\( \newcommand\Hz{\hat z}\)
\( \newcommand\HA{\hat A}\)
\( \newcommand\HB{\hat B}\)
\( \newcommand\HC{\hat C}\)
\( \newcommand\HD{\hat D}\)
\( \newcommand\HE{\hat E}\)
\( \newcommand\HF{\hat F}\)
\( \newcommand\HG{\hat G}\)
\( \newcommand\HH{\hat H}\)
\( \newcommand\HI{\hat I}\)
\( \newcommand\HJ{\hat J}\)
\( \newcommand\HK{\hat K}\)
\( \newcommand\HL{\hat L}\)
\( \newcommand\HM{\hat M}\)
\( \newcommand\HN{\hat N}\)
\( \newcommand\HO{\hat O}\)
\( \newcommand\HP{\hat P}\)
\( \newcommand\HQ{\hat Q}\)
\( \newcommand\HR{\hat R}\)
\( \newcommand\HS{\hat S}\)
\( \newcommand\HT{\hat T}\)
\( \newcommand\HU{\hat U}\)
\( \newcommand\HV{\hat V}\)
\( \newcommand\HW{\hat W}\)
\( \newcommand\HX{\hat X}\)
\( \newcommand\HY{\hat Y}\)
\( \newcommand\HZ{\hat Z}\)
\( \newcommand\Halpha{\hat\alpha}\)
\( \newcommand\Hbeta{\hat\beta}\)
\( \newcommand\Hgamma{\hat\gamma}\)
\( \newcommand\Hdelta{\hat\delta}\)
\( \newcommand\Hepsilon{\hat\epsilon}\)
\( \newcommand\Hvarepsilon{\hat\varepsilon}\)
\( \newcommand\Hzeta{\hat\zeta}\)
\( \newcommand\Heta{\hat\eta}\)
\( \newcommand\Htheta{\hat\theta}\)
\( \newcommand\Hvartheta{\hat\vartheta}\)
\( \newcommand\Hiota{\hat\iota}\)
\( \newcommand\Hkappa{\hat\kappa}\)
\( \newcommand\Hlambda{\hat\lambda}\)
\( \newcommand\Hmu{\hat\mu}\)
\( \newcommand\Hnu{\hat\nu}\)
\( \newcommand\Hxi{\hat\xi}\)
\( \newcommand\Hom{\hat\omicron}\)
\( \newcommand\Hpi{\hat\pi}\)
\( \newcommand\Hvarpi{\hat\varpi}\)
\( \newcommand\Hrho{\hat\rho}\)
\( \newcommand\Hvarrho{\hat\varrho}\)
\( \newcommand\Hsigma{\hat\sigma}\)
\( \newcommand\Hvarsigma{\hat\varsigma}\)
\( \newcommand\Htau{\var\tau}\)
\( \newcommand\Hupsilon{\hat\upsilon}\)
\( \newcommand\Hphi{\hat\phi}\)
\( \newcommand\Hvarphi{\hat\varphi}\)
\( \newcommand\Hchi{\hat\chi}\)
\( \newcommand\Hxhi{\hat\xhi}\)
\( \newcommand\Hpsi{\hat\psi}\)
\( \newcommand\Homega{\hat\omega}\)
\( \newcommand\HGamma{\hat\Gamma}\)
\( \newcommand\HDelta{\hat\Delta}\)
\( \newcommand\HTheta{\hat\Theta}\)
\( \newcommand\HLambda{\hat\Lambda}\)
\( \newcommand\HXi{\hat\Xi}\)
\( \newcommand\HPi{\hat\Pi}\)
\( \newcommand\HSigma{\hat\Sigma}\)
\( \newcommand\HUps{\hat\Upsilon}\)
\( \newcommand\HPhi{\hat\Phi}\)
\( \newcommand\HPsi{\hat\Psi}\)
\( \newcommand\HOmega{\hat\Omega}\)
\( \newcommand\xhat{\hat\Bx}\)
\( \newcommand\yhat{\hat\By}\)
\( \newcommand\zhat{\hat\Bz}\)
\( \newcommand\ehat{\hat\Be}\)
\( \newcommand\khat{\hat\Bk}\)
\( \newcommand\nhat{\hat\Bn}\)
\( \newcommand\rhat{\hat\Br}\)
\( \newcommand\phihat{\hat\Bphi}\)
\( \newcommand\thetahat{\hat\Btheta}\)
\( \newcommand\MA{\mathbb A}\)
\( \newcommand\MB{\mathbb B}\)
\( \newcommand\MC{\mathbb C}\)
\( \newcommand\MD{\mathbb D}\)
\( \newcommand\ME{\mathbb E}\)
\( \newcommand\MF{\mathbb F}\)
\( \newcommand\MG{\mathbb G}\)
\( \newcommand\MH{\mathbb H}\)
\( \newcommand\MI{\mathbb I}\)
\( \newcommand\MJ{\mathbb J}\)
\( \newcommand\MK{\mathbb K}\)
\( \newcommand\ML{\mathbb L}\)
\( \newcommand\MM{\mathbb M}\)
\( \newcommand\MN{\mathbb N}\)
\( \newcommand\MO{\mathbb O}\)
\( \newcommand\MP{\mathbb P}\)
\( \newcommand\MQ{\mathbb Q}\)
\( \newcommand\MR{\mathbb R}\)
\( \newcommand\MS{\mathbb S}\)
\( \newcommand\MT{\mathbb T}\)
\( \newcommand\MU{\mathbb U}\)
\( \newcommand\MV{\mathbb V}\)
\( \newcommand\MW{\mathbb W}\)
\( \newcommand\MX{\mathbb X}\)
\( \newcommand\MY{\mathbb Y}\)
\( \newcommand\MZ{\mathbb Z}\)
\( \newcommand\CA{\mathcal A}\)
\( \newcommand\CB{\mathcal B}\)
\( \newcommand\CC{\mathcal C}\)
\( \newcommand\CD{\mathcal D}\)
\( \newcommand\CE{\mathcal E}\)
\( \newcommand\CF{\mathcal F}\)
\( \newcommand\CG{\mathcal G}\)
\( \newcommand\CH{\mathcal H}\)
\( \newcommand\CI{\mathcal I}\)
\( \newcommand\CJ{\mathcal J}\)
\( \newcommand\CK{\mathcal K}\)
\( \newcommand\CL{\mathcal L}\)
\( \newcommand\CM{\mathcal M}\)
\( \newcommand\CN{\mathcal N}\)
\( \newcommand\CO{\mathcal O}\)
\( \newcommand\CP{\mathcal P}\)
\( \newcommand\CQ{\mathcal Q}\)
\( \newcommand\CR{\mathcal R}\)
\( \newcommand\CS{\mathcal S}\)
\( \newcommand\CT{\mathcal T}\)
\( \newcommand\CU{\mathcal U}\)
\( \newcommand\CV{\mathcal V}\)
\( \newcommand\CW{\mathcal W}\)
\( \newcommand\CX{\mathcal X}\)
\( \newcommand\CY{\mathcal Y}\)
\( \newcommand\CZ{\mathcal Z}\)
\( \newcommand\Fa{\mathfrak a}\)
\( \newcommand\Fb{\mathfrak b}\)
\( \newcommand\Fc{\mathfrak c}\)
\( \newcommand\Fd{\mathfrak d}\)
\( \newcommand\Fe{\mathfrak e}\)
\( \newcommand\Ff{\mathfrak f}\)
\( \newcommand\Fg{\mathfrak g}\)
\( \newcommand\Fh{\mathfrak h}\)
\( \newcommand\Fi{\mathfrak i}\)
\( \newcommand\Fj{\mathfrak j}\)
\( \newcommand\Fk{\mathfrak k}\)
\( \newcommand\Fl{\mathfrak l}\)
\( \newcommand\Fm{\mathfrak m}\)
\( \newcommand\Fn{\mathfrak n}\)
\( \newcommand\Fo{\mathfrak o}\)
\( \newcommand\Fp{\mathfrak p}\)
\( \newcommand\Fq{\mathfrak q}\)
\( \newcommand\Fr{\mathfrak r}\)
\( \newcommand\Fs{\mathfrak s}\)
\( \newcommand\Ft{\mathfrak t}\)
\( \newcommand\Fu{\mathfrak u}\)
\( \newcommand\Fv{\mathfrak v}\)
\( \newcommand\Fw{\mathfrak w}\)
\( \newcommand\Fx{\mathfrak x}\)
\( \newcommand\Fy{\mathfrak y}\)
\( \newcommand\Fz{\mathfrak z}\)
\( \newcommand\FA{\mathfrak A}\)
\( \newcommand\FB{\mathfrak B}\)
\( \newcommand\FC{\mathfrak C}\)
\( \newcommand\FD{\mathfrak D}\)
\( \newcommand\FE{\mathfrak E}\)
\( \newcommand\FF{\mathfrak F}\)
\( \newcommand\FG{\mathfrak G}\)
\( \newcommand\FH{\mathfrak H}\)
\( \newcommand\FI{\mathfrak I}\)
\( \newcommand\FJ{\mathfrak J}\)
\( \newcommand\FK{\mathfrak K}\)
\( \newcommand\FL{\mathfrak L}\)
\( \newcommand\FM{\mathfrak M}\)
\( \newcommand\FN{\mathfrak N}\)
\( \newcommand\FO{\mathfrak O}\)
\( \newcommand\FP{\mathfrak P}\)
\( \newcommand\FQ{\mathfrak Q}\)
\( \newcommand\FR{\mathfrak R}\)
\( \newcommand\FS{\mathfrak S}\)
\( \newcommand\FT{\mathfrak T}\)
\( \newcommand\FU{\mathfrak U}\)
\( \newcommand\FV{\mathfrak V}\)
\( \newcommand\FW{\mathfrak W}\)
\( \newcommand\FX{\mathfrak X}\)
\( \newcommand\FY{\mathfrak Y}\)
\( \newcommand\FZ{\mathfrak Z}\)
\( \newcommand\Da{\dot a}\)
\( \newcommand\Db{\dot b}\)
\( \newcommand\Dc{\dot c}\)
\( \newcommand\Dd{\dot d}\)
\( \newcommand\De{\dot e}\)
\( \newcommand\Df{\dot f}\)
\( \newcommand\Dg{\dot g}\)
\( \newcommand\Dh{\dot h}\)
\( \newcommand\Di{\dot \imath}\)
\( \newcommand\Dj{\dot \jmath}\)
\( \newcommand\Dk{\dot k}\)
\( \newcommand\Dl{\dot l}\)
\( \newcommand\Dm{\dot m}\)
\( \newcommand\Dn{\dot n}\)
\( \newcommand\Do{\dot o}\)
\( \newcommand\Dp{\dot p}\)
\( \newcommand\Dq{\dot q}\)
\( \newcommand\Dr{\dot r}\)
\( \newcommand\Ds{\dot s}\)
\( \newcommand\Dt{\dot t}\)
\( \newcommand\Du{\dot u}\)
\( \newcommand\Dv{\dot v}\)
\( \newcommand\Dw{\dot w}\)
\( \newcommand\Dx{\dot x}\)
\( \newcommand\Dy{\dot y}\)
\( \newcommand\Dz{\dot z}\)
\( \newcommand\DA{\dot A}\)
\( \newcommand\DB{\dot B}\)
\( \newcommand\DC{\dot C}\)
\( \newcommand\DD{\dot D}\)
\( \newcommand\DE{\dot E}\)
\( \newcommand\DF{\dot F}\)
\( \newcommand\DG{\dot G}\)
\( \newcommand\DH{\dot H}\)
\( \newcommand\DI{\dot I}\)
\( \newcommand\DJ{\dot J}\)
\( \newcommand\DK{\dot K}\)
\( \newcommand\DL{\dot L}\)
\( \newcommand\DM{\dot M}\)
\( \newcommand\DN{\dot N}\)
\( \newcommand\DO{\dot O}\)
\( \newcommand\DP{\dot P}\)
\( \newcommand\DQ{\dot Q}\)
\( \newcommand\DR{\dot R}\)
\( \newcommand\DS{\dot S}\)
\( \newcommand\DT{\dot T}\)
\( \newcommand\DU{\dot U}\)
\( \newcommand\DV{\dot V}\)
\( \newcommand\DW{\dot W}\)
\( \newcommand\DX{\dot X}\)
\( \newcommand\DY{\dot Y}\)
\( \newcommand\DZ{\dot Z}\)
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dmu{\dot\mu}\)
\( \newcommand\Dnu{\dot\nu}\)
\( \newcommand\Dxi{\dot\xi}\)
\( \newcommand\Dom{\dot\omicron}\)
\( \newcommand\Dpi{\dot\pi}\)
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Drho{\dot\rho}\)
\( \newcommand\Dvarrho{\dot\varrho}\)
\( \newcommand\Dsigma{\dot\sigma}\)
\( \newcommand\Dvarsigma{\dot\varsigma}\)
\( \newcommand\Dtau{\var\tau}\)
\( \newcommand\Dupsilon{\dot\upsilon}\)
\( \newcommand\Dphi{\dot\phi}\)
\( \newcommand\Dvarphi{\dot\varphi}\)
\( \newcommand\Dchi{\dot\chi}\)
\( \newcommand\Dpsi{\dot\psi}\)
\( \newcommand\Domega{\dot\omega}\)
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DLambda{\dot\Lambda}\)
\( \newcommand\DXi{\dot\Xi}\)
\( \newcommand\DPi{\dot\Pi}\)
\( \newcommand\DSigma{\dot\Sigma}\)
\( \newcommand\DUps{\dot\Upsilon}\)
\( \newcommand\DPhi{\dot\Phi}\)
\( \newcommand\DPsi{\dot\Psi}\)
\( \newcommand\DOmega{\dot\Omega}\)
\( \newcommand\Va{\vec a}\)
\( \newcommand\Vb{\vec b}\)
\( \newcommand\Vc{\vec c}\)
\( \newcommand\Vd{\vec d}\)
\( \newcommand\Ve{\vec e}\)
\( \newcommand\Vf{\vec f}\)
\( \newcommand\Vg{\vec g}\)
\( \newcommand\Vh{\vec h}\)
\( \newcommand\Vi{\vec \imath}\)
\( \newcommand\Vj{\vec \jmath}\)
\( \newcommand\Vk{\vec k}\)
\( \newcommand\Vl{\vec l}\)
\( \newcommand\Vm{\vec m}\)
\( \newcommand\Vn{\vec n}\)
\( \newcommand\Vo{\vec o}\)
\( \newcommand\Vp{\vec p}\)
\( \newcommand\Vq{\vec q}\)
\( \newcommand\Vr{\vec r}\)
\( \newcommand\Vs{\vec s}\)
\( \newcommand\Vt{\vec t}\)
\( \newcommand\Vu{\vec u}\)
\( \newcommand\Vv{\vec v}\)
\( \newcommand\Vw{\vec w}\)
\( \newcommand\Vx{\vec x}\)
\( \newcommand\Vy{\vec y}\)
\( \newcommand\Vz{\vec z}\)
\( \newcommand\VA{\vec A}\)
\( \newcommand\VB{\vec B}\)
\( \newcommand\VC{\vec C}\)
\( \newcommand\VD{\vec D}\)
\( \newcommand\VE{\vec E}\)
\( \newcommand\VF{\vec F}\)
\( \newcommand\VG{\vec G}\)
\( \newcommand\VH{\vec H}\)
\( \newcommand\VI{\vec I}\)
\( \newcommand\VJ{\vec J}\)
\( \newcommand\VK{\vec K}\)
\( \newcommand\VL{\vec L}\)
\( \newcommand\VM{\vec M}\)
\( \newcommand\VN{\vec N}\)
\( \newcommand\VO{\vec O}\)
\( \newcommand\VP{\vec P}\)
\( \newcommand\VQ{\vec Q}\)
\( \newcommand\VR{\vec R}\)
\( \newcommand\VS{\vec S}\)
\( \newcommand\VT{\vec T}\)
\( \newcommand\VU{\vec U}\)
\( \newcommand\VV{\vec V}\)
\( \newcommand\VW{\vec W}\)
\( \newcommand\VX{\vec X}\)
\( \newcommand\VY{\vec Y}\)
\( \newcommand\VZ{\vec Z}\)
\( \newcommand\Valpha{\vec\alpha}\)
\( \newcommand\Vbeta{\vec\beta}\)
\( \newcommand\Vgamma{\vec\gamma}\)
\( \newcommand\Vdelta{\vec\delta}\)
\( \newcommand\Vepsilon{\vec\epsilon}\)
\( \newcommand\Vvarepsilon{\vec\varepsilon}\)
\( \newcommand\Vzeta{\vec\zeta}\)
\( \newcommand\Veta{\vec\eta}\)
\( \newcommand\Vtheta{\vec\theta}\)
\( \newcommand\Vvartheta{\vec\vartheta}\)
\( \newcommand\Viota{\vec\iota}\)
\( \newcommand\Vkappa{\vec\kappa}\)
\( \newcommand\Vlambda{\vec\lambda}\)
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VTheta{\vec\Theta}\)
\( \newcommand\VLambda{\vec\Lambda}\)
\( \newcommand\VXi{\vec\Xi}\)
\( \newcommand\VPi{\vec\Pi}\)
\( \newcommand\VSigma{\vec\Sigma}\)
\( \newcommand\VUps{\vec\Upsilon}\)
\( \newcommand\VPhi{\vec\Phi}\)
\( \newcommand\VPsi{\vec\Psi}\)
\( \newcommand\VOmega{\vec\Omega}\)
\( \newcommand\BA{\mib A}\)
\( \newcommand\BB{\mib B}\)
\( \newcommand\BC{\mib C}\)
\( \newcommand\BD{\mib D}\)
\( \newcommand\BE{\mib E}\)
\( \newcommand\BF{\mib F}\)
\( \newcommand\BG{\mib G}\)
\( \newcommand\BH{\mib H}\)
\( \newcommand\BI{\mib I}}\)
\( \newcommand\BJ{\mib J}\)
\( \newcommand\BK{\mib K}\)
\( \newcommand\BL{\mib L}\)
\( \newcommand\BM{\mib M}\)
\( \newcommand\BN{\mib N}\)
\( \newcommand\BO{\mib O}\)
\( \newcommand\BP{\mib P}\)
\( \newcommand\BQ{\mib Q}\)
\( \newcommand\BR{\mib R}\)
\( \newcommand\BS{\mib S}\)
\( \newcommand\BT{\mib T}\)
\( \newcommand\BU{\mib U}\)
\( \newcommand\BV{\mib V}\)
\( \newcommand\BW{\mib W}\)
\( \newcommand\BX{\mib X}\)
\( \newcommand\BY{\mib Y}\)
\( \newcommand\BZ{\mib Z}\)
\( \newcommand\Ba{\mib a}\)
\( \newcommand\Bb{\mib b}\)
\( \newcommand\Bc{\mib c}\)
\( \newcommand\Bd{\mib d}\)
\( \newcommand\Be{\mib e}\)
\( \newcommand\Bf{\mib f}\)
\( \newcommand\Bg{\mib g}\)
\( \newcommand\Bh{\mib h}\)
\( \newcommand\Bi{\mib i}\)
\( \newcommand\Bj{\mib j}\)
\( \newcommand\Bk{\mib k}\)
\( \newcommand\Bl{\mib l}\)
\( \newcommand\Bm{\mib m}\)
\( \newcommand\Bn{\mib n}\)
\( \newcommand\Bo{\mib o}\)
\( \newcommand\Bp{\mib p}\)
\( \newcommand\Bq{\mib q}\)
\( \newcommand\Br{\mib r}\)
\( \newcommand\Bs{\mib s}\)
\( \newcommand\Bt{\mib t}\)
\( \newcommand\Bu{\mib u}\)
\( \newcommand\Bv{\mib v}\)
\( \newcommand\Bw{\mib w}\)
\( \newcommand\Bx{\mib x}\)
\( \newcommand\By{\mib y}\)
\( \newcommand\Bz{\mib z}\)\)
\( \newcommand\vrh{\varrho}\)
\( \newcommand\vsig{\varsigma}\)
\( \newcommand\ups{\upsilon}\)
\( \newcommand\eps{\epsilon}\)
\( \newcommand\ve{\varepsilon}\)
\( \newcommand\vth{\vartheta}\)
\( \newcommand\vphi{\varphi}\)
\( \newcommand\xhi{\chi}\)
\( \newcommand\Ups{\Upsilon}\)
\( \newcommand\Balpha{\mib\alpha}\)
\( \newcommand\Bbeta{\mib\beta}\)
\( \newcommand\Bgamma{\mib\gamma}\)
\( \newcommand\Bdelta{\mib\delta}\)
\( \newcommand\Beps{\mib\epsilon}\)
\( \newcommand\Bve{\mib\varepsilon}\)
\( \newcommand\Bzeta{\mib\zeta}\)
\( \newcommand\Beta{\mib\eta}\)
\( \newcommand\Btheta{\mib\theta}\)
\( \newcommand\Bvth{\mib\vartheta}\)
\( \newcommand\Biota{\mib\iota}\)
\( \newcommand\Bkappa{\mib\kappa}\)
\( \newcommand\Blambda{\mib\lambda}\)
\( \newcommand\Bmu{\mib\mu}\)
\( \newcommand\Bnu{\mib\nu}\)
\( \newcommand\Bxi{\mib\xi}\)
\( \newcommand\Bom{\mib\omicron}\)
\( \newcommand\Bpi{\mib\pi}\)
\( \newcommand\Bvarpi{\mib\varpi}\)
\( \newcommand\Brho{\mib\rho}\)
\( \newcommand\Bvrh{\mib\varrho}\)
\( \newcommand\Bsigma{\mib\sigma}\)
\( \newcommand\Bvsig{\mib\varsigma}\)
\( \newcommand\Btau{\mib\tau}\)
\( \newcommand\Bups{\mib\upsilon}\)
\( \newcommand\Bphi{\mib\phi}\)
\( \newcommand\Bvphi{\mib\vphi}\)
\( \newcommand\Bchi{\mib\chi}\)
\( \newcommand\Bpsi{\mib\psi}\)
\( \newcommand\Bomega{\mib\omega}\)
\( \newcommand\BGamma{\mib\Gamma}\)
\( \newcommand\BDelta{\mib\Delta}\)
\( \newcommand\BTheta{\mib\Theta}\)
\( \newcommand\BLambda{\mib\Lambda}\)
\( \newcommand\BXi{\mib\Xi}\)
\( \newcommand\BPi{\mib\Pi}\)
\( \newcommand\BSigma{\mib\Sigma}\)
\( \newcommand\BUps{\mib\Upsilon}\)
\( \newcommand\BPhi{\mib\Phi}\)
\( \newcommand\BPsi{\mib\Psi}\)
\( \newcommand\BOmega{\mib\Omega}\)
\( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\)
\( \newcommand\RGamma{ \Gamma}\)
\( \newcommand\RDelta{ \Delta}\)
\( \newcommand\RTheta{ \Theta}\)
\( \newcommand\RLambda{ \Lambda}\)
\( \newcommand\RXi{ \Xi}\)
\( \newcommand\RPi{ \Pi}\)
\( \newcommand\RSigma{ \Sigma}\)
\( \newcommand\RUps{ \Upsilon}\)
\( \newcommand\RPhi{ \Phi}\)
\( \newcommand\RPsi{ \Psi}\)
\( \newcommand\ROmega{ \Omega}\)
\( \newcommand\RA{ A}\)
\( \newcommand\RB{ B}\)
\( \newcommand\RC{ C}\)
\( \newcommand\RD{ D}\)
\( \newcommand\RE{ E}\)
\( \newcommand\RF{ F}\)
\( \newcommand\RG{ G}\)
\( \newcommand\RH{ H}\)
\( \newcommand\RI{ I}\)
\( \newcommand\RJ{ J}\)
\( \newcommand\RK{ K}\)
\( \newcommand\RL{ L}\)
\( \newcommand { M}\)
\( \newcommand\RN{ N}\)
\( \newcommand\RO{ O}\)
\( \newcommand\RP{ P}\)
\( \newcommand\RQ{ Q}\)
\( \newcommand\RR{ R}\)
\( \newcommand\RS{ S}\)
\( \newcommand\RT{ T}\)
\( \newcommand\RU{ U}\)
\( \newcommand\RV{ V}\)
\( \newcommand\RW{ W}\)
\( \newcommand\RX{ X}\)
\( \newcommand\RY{ Y}\)
\( \newcommand\RZ{ Z}\)
\( \newcommand\Ra{ a}\)
\( \newcommand\Rb{ b}\)
\( \newcommand\Rc{ c}\)
\( \newcommand\Rd{ d}\)
\( \newcommand\Re{ e}\)
\( \newcommand\Rf{ f}\)
\( \newcommand\Rg{ g}\)
\( \newcommand\Rh{ h}\)
\( \newcommand\Ri{ i}\)
\( \newcommand\Rj{ j}\)
\( \newcommand\Rk{ k}\)
\( \newcommand\Rl{ l}\)
\( \newcommand { m}\)
\( \newcommand\Rn{ n}\)
\( \newcommand\Ro{ o}\)
\( \newcommand\Rp{ p}\)
\( \newcommand\Rq{ q}\)
\( \newcommand\Rr{ r}\)
\( \newcommand\Rs{ s}\)
\( \newcommand\Rt{ t}\)
\( \newcommand\Ru{ u}\)
\( \newcommand\Rv{ v}\)
\( \newcommand\Rw{ w}\)
\( \newcommand\Rx{ x}\)
\( \newcommand\Ry{ y}\)
\( \newcommand\Rz{ z}\)
\( \newcommand\BBA{\boldsymbol\RA}\)
\( \newcommand\BBB{\boldsymbol\RB}\)
\( \newcommand\BBC{\boldsymbol\RC}\)
\( \newcommand\BBD{\boldsymbol\RD}\)
\( \newcommand\BBE{\boldsymbol\RE}\)
\( \newcommand\BBF{\boldsymbol\RF}\)
\( \newcommand\BBG{\boldsymbol\RG}\)
\( \newcommand\BBH{\boldsymbol\RH}\)
\( \newcommand\BBI{\boldsymbol\RI}\)
\( \newcommand\BBJ{\boldsymbol\RJ}\)
\( \newcommand\BBK{\boldsymbol\RK}\)
\( \newcommand\BBL{\boldsymbol\RL}\)
\( \newcommand\BBM{\boldsymbol }\)
\( \newcommand\BBN{\boldsymbol\RN}\)
\( \newcommand\BBO{\boldsymbol\RO}\)
\( \newcommand\BBP{\boldsymbol\RP}\)
\( \newcommand\BBQ{\boldsymbol\RQ}\)
\( \newcommand\BBR{\boldsymbol\RR}\)
\( \newcommand\BBS{\boldsymbol\RS}\)
\( \newcommand\BBT{\boldsymbol\RT}\)
\( \newcommand\BBU{\boldsymbol\RU}\)
\( \newcommand\BBV{\boldsymbol\RV}\)
\( \newcommand\BBW{\boldsymbol\RW}\)
\( \newcommand\BBX{\boldsymbol\RX}\)
\( \newcommand\BBY{\boldsymbol\RY}\)
\( \newcommand\BBZ{\boldsymbol\RZ}\)
\( \newcommand\BBa{\boldsymbol\Ra}\)
\( \newcommand\BBb{\boldsymbol\Rb}\)
\( \newcommand\BBc{\boldsymbol\Rc}\)
\( \newcommand\BBd{\boldsymbol\Rd}\)
\( \newcommand\BBe{\boldsymbol\Re}\)
\( \newcommand\BBf{\boldsymbol\Rf}\)
\( \newcommand\BBg{\boldsymbol\Rg}\)
\( \newcommand\BBh{\boldsymbol\Rh}\}\)
\( \newcommand\BBi{\boldsymbol\Ri}\)
\( \newcommand\BBj{\boldsymbol\Rj}\)
\( \newcommand\BBk{\boldsymbol\Rk}\)
\( \newcommand\BBl{boldsymbol\Rl}\)
\( \newcommand\BBm{\boldsymbol }\)
\( \newcommand\BBn{\boldsymbol\Rn}\)
\( \newcommand\BBo{\boldsymbol\Ro}\)
\( \newcommand\BBp{\boldsymbol\Rp}\)
\( \newcommand\BBq{\boldsymbol\Rq}\)
\( \newcommand\BBr{\boldsymbol\Rr}\)
\( \newcommand\BBs{\boldsymbol\Rs}\)
\( \newcommand\BBt{\boldsymbol\Rt}\)
\( \newcommand\BBu{\boldsymbol\Ru}\)
\( \newcommand\BBv{\boldsymbol\Rv}\)
\( \newcommand\BBw{\boldsymbol\Rw}\)
\( \newcommand\BBx{\boldsymbol\Rx}\)
\( \newcommand\BBy{\boldsymbol\Ry}\)
\( \newcommand\BBz{\boldsymbol\Rz}\)
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
\( \newcommand\bnabla{\boldsymbol{\nabla}}\)
\( \newcommand\Bell{\boldsymbol\ell}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \newcommand\ns{^\vphantom{*}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\)
\( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\)
\( \newcommand\etc{\it etc.\/}\)
\( \newcommand\etal{\it et al.\/}\)
\( \newcommand\opcit{\it op. cit.\/}\)
\( \newcommand\ie{\it i.e.\/}\)
\( \newcommand\Ie{\it I.e.\/}\)
\( \newcommand\viz{\it viz.\/}\)
\( \newcommand\eg{\it e.g.\/}\)
\( \newcommand\Eg{\it E.g.\/}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \def\sss#1{\scriptscriptstyle #1}\)
\( \def\ss#1{\scriptstyle #1}\)
\( \def\ssr#1{\scriptstyle #1}\)
\( \def\ssf#1{\scriptstyle #1}\)
\( \newcommand\NA{N_{\ssr{\!A}}}\)
\( \newcommand\lala{\langle\!\langle}\)
\( \newcommand\rara{\rangle\!\rangle}\)
\( \newcommand\blan{\big\langle}\)
\( \newcommand\bran{\big\rangle}\)
\( \newcommand\Blan{\Big\langle}\)
\( \newcommand\Bran{\Big\rangle}\)
\( \newcommand\intl{\int\limits}\)
\( \newcommand\half{\frac{1}{2}}\)
\( \newcommand\third{\frac{1}{3}}\)
\( \newcommand\fourth{\frac{1}{4}}\)
\( \newcommand\eighth{\frac{1}{8}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\)
\( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\)
\( \newcommand\det{\mathop{\textsf{det}}\,}\)
\( \def\tket#1{|  #1 \rangle}\)
\( \def\tbra#1{\langle #1|}\)
\( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\)
\( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\)
\( \def\sket#1{|  \, #1 \,  \rangle}\)
\( \def\sbra#1{\langle \,  #1 \, |}\)
\( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\)
\( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\)
\(\def\ket#1{\big| \, #1\, \big\rangle}\)
\( \def\bra#1{\big\langle \, #1 \, \big|}\)
\( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\)
\( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\)
\( \newcommand\pz{\partial}\)
\( \newcommand\pzb{\bar{\partial}}\)
\( \newcommand\svph{\vphantom{\int}}\)
\( \newcommand\vph{\vphantom{\sum_i}}\)
\( \newcommand\bvph{\vphantom{\sum_N^N}}\)
\( \newcommand\nd{^{\vphantom{\dagger}}}\)
\( \newcommand\ns{^{\vphantom{*}}}\)
\( \newcommand\yd{^\dagger}\)
\( \newcommand\zb{\bar z}\)
\( \newcommand\zdot{\dot z}\)
\( \newcommand\zbdot{\dot{\bar z}}\)
\( \newcommand\kB{k_{\sss{B}}}\)
\( \newcommand\kT{k_{\sss{B}}T}\)
\( \newcommand\gtau{g_\tau}\)
\( \newcommand\Htil{\tilde H}\)
\( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\)
\( \newcommand\pairm{(\phi\nd_0,J)}\)
\( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\)
\( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\)
\( \newcommand\pair{(\phi,J)}\)
\( \newcommand\Hz{H\nd_0}\)
\( \newcommand\Ho{H\nd_1}\)
\( \newcommand\Htz{\Htil\nd_0}\)
\( \newcommand\Hto{\Htil\nd_1}\)
\( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\)
\( \newcommand\csch{\,{ csch\,}}\)
\( \newcommand\ctnh{\,{ ctnh\,}}\)
\( \newcommand\ctn{\,{ ctn\,}}\)
\( \newcommand\sgn{\,{ sgn\,}}\)
\( \def\tmapright#1{\xrightarrow \limits^{#1}}\)
\( \def\bmapright#1{\xrightarrow\limits_{#1}}\)
\( \newcommand\hfb{\hfill\break}\)
\( \newcommand\Rep{\textsf{Re}\,}\)
\( \newcommand\Imp{\textsf{Im}\,}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\)
\( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\)
\( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

\( \def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}\)
\( \def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}\)
\( \def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}\)
\( \def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}\)
\( \newcommand\subA{\ns_\ssr{A}}\)
\( \newcommand\subB{\ns_\ssr{B}}\)
\( \newcommand\subC{\ns_\ssr{C}}\)
\( \newcommand\subD{\ns_\ssr{D}}\)
\( \newcommand\subAB{\ns_\ssr{AB}}\)
\( \newcommand\subBC{\ns_\ssr{BC}}\)
\( \newcommand\subCD{\ns_\ssr{CD}}\)
\( \newcommand\subDA{\ns_\ssr{DA}}\)
\( \def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }\)
\( \def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}\)
\( \newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}\)
\( \newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}\)
\( \newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}\)
\( \newcommand\cds{\,\bullet\,}\)
\( \newcommand\ccs{\,\circ\,}\)
\( \newcommand\nsub{_{\vphantom{\dagger}}}\)
\( \newcommand\rhohat{\hat\rho}\)
\( \newcommand\vrhhat{\hat\vrh}\)
\( \newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}\)
\( \newcommand\brangle{\big\rangle}\)
\( \newcommand\blangle{\big\langle}\)
\( \newcommand\vet{\tilde\ve}\)
\( \newcommand\zbar{\bar z}\)
\( \newcommand\ftil{\tilde f}\)
\( \newcommand\XBE{\RXi\ns_\ssr{BE}}\)
\( \newcommand\XFD{\RXi\ns_\ssr{FD}}\)
\( \newcommand\OBE{\Omega\ns_\ssr{BE}}\)
\( \newcommand\OFD{\Omega\ns_\ssr{FD}}\)
\( \newcommand\veF{\ve\ns_\RF}\)
\( \newcommand\kF{k\ns_\RF}\)
\( \newcommand\kFu{k\ns_{\RF\uar}}\)
\( \newcommand\SZ{\textsf Z}}\) \( \newcommand\kFd{k\ns_{\RF\dar}\)
\( \newcommand\muB{\mu\ns_\ssr{B}}\)
\( \newcommand\mutB{\tilde\mu}\ns_\ssr{B}\)
\( \newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}\)
\( \newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}\)
\( \newcommand\xhiOZ{\xhi^\ssr{OZ}}\)
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\jhz{\HJ(0)}\)
\( \newcommand\nda{\nd_\alpha}\)
\( \newcommand\ndap{\nd_{\alpha'}}\)
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/02:_Thermodynamics/2.04:_The_First_Law_of_Thermodynamics), /content/body/p/span, line 1, column 23

\)
\( \newcommand\msa{m\ns_\ssr{A}}\)
\( \newcommand\msb{m\ns_\ssr{B}}\)
\( \newcommand\mss{m\ns_\Rs}\)
\( \newcommand\HBx{\hat\Bx}\)
\( \newcommand\HBy{\hat\By}\)
\( \newcommand\HBz{\hat\Bz}\)
\( \newcommand\thm{\theta\ns_m}\)
\( \newcommand\thp{\theta\ns_\phi}\)
\( \newcommand\mtil{\widetilde m}\)
\( \newcommand\phitil{\widetilde\phi}\)
\( \newcommand\delf{\delta\! f}\)
\( \newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}\)
\( \newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}\)
\( \newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}\)
\( \newcommand\vbar{\bar v}\)
\( \newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}\)
\( \newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}\)
\( \newcommand\gla{g\nd_{\RLambda\nd}}\)
\( \newcommand\TA{T\ns_\ssr{A}}\)
\( \newcommand\TB{T\ns_\ssr{B}}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \newcommand\NS{N\ns_{\textsf S}}\)

Conservation of energy

The first law is a statement of energy conservation, and is depicted in Fig. [firstlaw]. It says, quite simply, that during a thermodynamic process, the change in a system’s internal energy \(E\) is given by the heat energy \(Q\) added to the system, minus the work \(W\) done by the system: \[\RDelta E = Q-W\ .\] The differential form of this, the First Law of Thermodynamics, is \[dE=\dbar Q - \dbar W\ .\] We use the symbol \(\dbar\) in the differentials \(\dbar Q\) and \(\dbar W\) to remind us that these are inexact differentials. The energy \(E\), however, is a state function, hence \(dE\) is an exact differential.

Consider a volume \(V\) of fluid held in a flask, initially at temperature \(T\ns_0\), and held at atmospheric pressure. The internal energy is then \(E\ns_0=E(T\ns_0,p,V)\). Now let us contemplate changing the temperature in two different ways. The first method (A) is to place the flask on a hot plate until the temperature of the fluid rises to a value \(T\ns_1\). The second method (B) is to stir the fluid vigorously. In the first case, we add heat \(Q\subA>0\) but no work is done, so \(W\subA=0\). In the second case, if we thermally insulate the flask and use a stirrer of very low thermal conductivity, then no heat is added, \(Q\subB=0\). However, the stirrer does work \(-W\subB>0\) on the fluid (remember \(W\) is the work done by the system). If we end up at the same temperature \(T\ns_1\), then the final energy is \(E\ns_1=E(T\ns_1,p,V)\) in both cases. We then have \[\RDelta E = E\ns_1-E\ns_0 = Q\subA = -W\subB\ .\]

[firstlaw] The first law of thermodynamics is a statement of energy conservation.

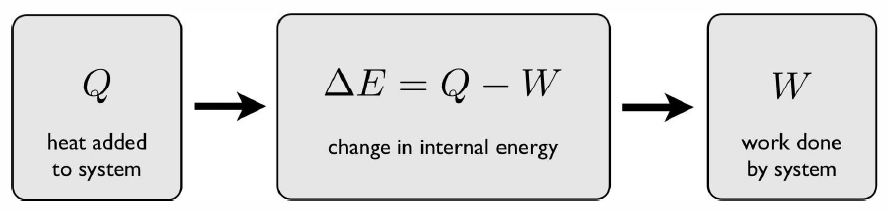
It also follows that for any cyclic transformation, where the state variables are the same at the beginning and the end, we have \[\RDelta E\ns_{cyclic}=Q-W=0 \quad\Longrightarrow\quad Q=W \quad\hbox{(cyclic)}\ .\]

Single component systems

A single component system is specified by three state variables. In many applications, the total number of particles \(N\) is conserved, so it is useful to take \(N\) as one of the state variables. The remaining two can be \((T,V)\) or \((T,p)\) or \((p,V)\). The differential form of the first law says \[\begin{aligned} dE&=\dbar Q-\dbar W\nonumber\\ &=\dbar Q - p\,dV + \mu\,dN\ . \label{DFL}\end{aligned}\] The quantity \(\mu\) is called the chemical potential. We ask: how much heat is required in order to make an infinitesimal change in temperature, pressure, volume, or particle number? We start by rewriting Equation [DFL] as \[\dbar Q=dE + p\,dV -\mu\,dN\ .\] We now must roll up our sleeves and do some work with partial derivatives.

\(\bullet\) \((T,V,N)\) systems : If the state variables are \((T,V,N)\), we write \[dE=\pabc{E}{T}{V,N}dT + \pabc{E}{V}{T,N}dV + \pabc{E}{N}{T,V}dN\ .\] Then \[\dbar Q=\pabc{E}{T}{V,N}dT + \Bigg[\pabc{E}{V}{T,N}+p\Bigg] dV + \Bigg[\pabc{E}{N}{T,V}-\mu\Bigg]dN\ . \label{QTVN}\]

\(\bullet\) \((T,p,N)\) systems : If the state variables are \((T,p,N)\), we write \[dE=\pabc{E}{T}{p,N}dT + \pabc{E}{p}{T,N}dp+ \pabc{E}{N}{T,p}dN\ .\] We also write \[dV=\pabc{V}{T}{p,N}dT + \pabc{V}{p}{T,N}dp + \pabc{V}{N}{T,p}dN\ .\] Then \[\begin{split} \dbar Q&=\Bigg[\pabc{E}{T}{p,N}+p\pabc{V}{T}{p,N}\Bigg] dT + \Bigg[\pabc{E}{p}{T,N}+p\pabc{V}{p}{T,N}\Bigg] dp\\ &\qquad\qquad+\Bigg[\pabc{E}{N}{T,p}+ p\pabc{V}{N}{T,p} -\mu\Bigg]dN\ . \label{QTpN} \end{split}\]

\(\bullet\) \((p,V,N)\) systems : If the state variables are \((p,V,N)\), we write \[dE=\pabc{E}{p}{V,N}dp + \pabc{E}{V}{p,N}dV + \pabc{E}{N}{p,V}dN\ .\] Then \[\dbar Q=\pabc{E}{p}{V,N}dp + \Bigg[\pabc{E}{V}{p,N}+p\Bigg] dV + \Bigg[\pabc{E}{N}{p,V}-\mu\Bigg]dN\ . \label{QpVN}\]

The heat capacity of a body, \(C\), is by definition the ratio \(\dbar Q/dT\) of the amount of heat absorbed by the body to the associated infinitesimal change in temperature \(dT\). The heat capacity will in general be different if the body is heated at constant volume or at constant pressure. Setting \(dV=0\) gives, from Equation [QTVN], \[C\ns_{V,N}=\bigg({\dbar Q\over dT}\bigg)\ns_{V,N}=\pabc{E}{T}{V,N}\ . \label{cveqn}\] Similarly, if we set \(dp=0\), then Equation [QTpN] yields \[C\ns_{p,N}=\bigg({\dbar Q\over dT}\bigg)\ns_{p,N}=\pabc{E}{T}{p,N}+ p \pabc{V}{T}{p,N}\ . \label{cpeqn}\] Unless explicitly stated as otherwise, we shall assume that \(N\) is fixed, and will write \(C\ns_V\) for \(C\ns_{V,N}\) and \(C\ns_p\) for \(C\ns_{p,N}\).

[cptab] Specific heat (at \(25^\circ\,\)C, unless otherwise noted) of some common substances. (Source: Wikipedia.)

	\(c\ns_p\)	\({\tilde c}\ns_p\)		\(c\ns_p\)	\({\tilde c}\ns_p\)
SUBSTANCE	(\(\RJ/{mol}\,\RK\))	(\(\RJ/{g}\,\RK\))	SUBSTANCE	(\(\RJ/{mol}\,\RK\))	(\(\RJ/{g}\,\RK\))
Air	29.07	1.01	\(\RH\ns_2\RO\) (\(25^\circ\,\)C)	75.34	4.181
Aluminum	24.2	0.897	\(\RH\ns_2\RO\) (\(100_+^\circ\,\)C)	37.47	2.08
Copper	24.47	0.385	Iron	25.1	0.450
\(\RC\RO\ns_2\)	36.94	0.839	Lead	26.4	0.127
Diamond	6.115	0.509	Lithium	24.8	3.58
Ethanol	112	2.44	Neon	20.786	1.03
Gold	25.42	0.129	Oxygen	29.38	0.918
Helium	20.786	5.193	Paraffin (wax)	900	2.5
Hydrogen	28.82	5.19	Uranium	27.7	0.116
\(\RH\ns_2\RO\) (\(-10^\circ\,\)C)	38.09	2.05	Zinc	25.3	0.387

The units of heat capacity are energy divided by temperature, \(\RJ/\RK\). The heat capacity is an extensive quantity, scaling with the size of the system. If we divide by the number of moles \(N/\NA\), we obtain the molar heat capacity, sometimes called the molar specific heat: \(c=C/\nu\), where \(\nu=N/\NA\) is the number of moles of substance. Specific heat is also sometimes quoted in units of heat capacity per gram of substance. We shall define \[{\tilde c}={C\over m N}={c\over M} = { \hbox{heat capacity per mole}\over \hbox{mass per mole}}\ .\] Here \(m\) is the mass per particle and \(M\) is the mass per mole: \(M=\NA\, m\).

Suppose we raise the temperature of a body from \(T=\TA\) to \(T=\TB\). How much heat is required? We have \[Q=\int\limits_\TA^\TB\!\!dT\,C(T)\ ,\] where \(C=C\ns_V\) or \(C=C\ns_p\) depending on whether volume or pressure is held constant. For ideal gases, as we shall discuss below, \(C(T)\) is constant, and thus \[Q=C(\TB-\TA) \quad\Longrightarrow\quad \TB=\TA+{Q\over C}\ .\]

In metals at very low temperatures one finds \(C=\gamma T\), where \(\gamma\) is a constant⁶. We then have \[\begin{aligned} Q&=\int\limits_\TA^\TB\!\!dT\,C(T)=\half\gamma\big(T_\ssr{B}^2 - T_\ssr{A}^2\big)\\ \TB&=\sqrt{T_\ssr{A}^2 + 2\gamma^{-1} Q}\ .\end{aligned}\]

Ideal gases

The ideal gas equation of state is \(pV=N\kT\). In order to invoke the formulae in Equations \ref{QTVN}, \ref{QTpN}, and \ref{QpVN}, we need to know the state function \(E(T,V,N)\). A landmark experiment by Joule in the mid-19th century established that the energy of a low density gas is independent of its volume⁷. Essentially, a gas at temperature \(T\) was allowed to freely expand from one volume \(V\) to a larger volume \(V'>V\), with no added heat \(Q\) and no work \(W\) done. Therefore the energy cannot change. What Joule found was that the temperature also did not change. This means that \(E(T,V,N)=E(T,N)\) cannot be a function of the volume.

[CVH2] Heat capacity \(C_V\) for one mole of hydrogen (\(\RH_2\)) gas. At the lowest temperatures, only translational degrees of freedom are relevant, and \(f=3\). At around \(200\,\RK\), two rotational modes are excitable and \(f=5\). Above \(1000\,\RK\), the vibrational excitations begin to contribute. Note the logarithmic temperature scale. (Data from H. W. Wooley et al., Jour. Natl. Bureau of Standards, 41, 379 (1948).)

Since \(E\) is extensive, we conclude that \[E(T,V,N)=\nu\,\ve(T) \ ,\] where \(\nu=N/\NA\) is the number of moles of substance. Note that \(\nu\) is an extensive variable. From eqns. [cveqn] and [cpeqn], we conclude \[C\ns_V(T)=\nu\,\ve'(T) \qquad,\qquad C\ns_p(T)=C\ns_V(T) + \nu R\ ,\] where we invoke the ideal gas law to obtain the second of these. Empirically it is found that \(C\ns_V(T)\) is temperature independent over a wide range of \(T\), far enough from boiling point. We can then write \(C\ns_V=\nu\, c\ns_V\), where \(\nu\equiv N/\NA\) is the number of moles, and where \(c\ns_V\) is the molar heat capacity. We then have \[c\ns_p=c\ns_V+R\ ,\] where \(R=\NA\kB = 8.31457\,\RJ/{mol}\,\RK\) is the gas constant. We denote by \(\gamma=c\ns_p/c\ns_V\) the ratio of specific heat at constant pressure and at constant volume.

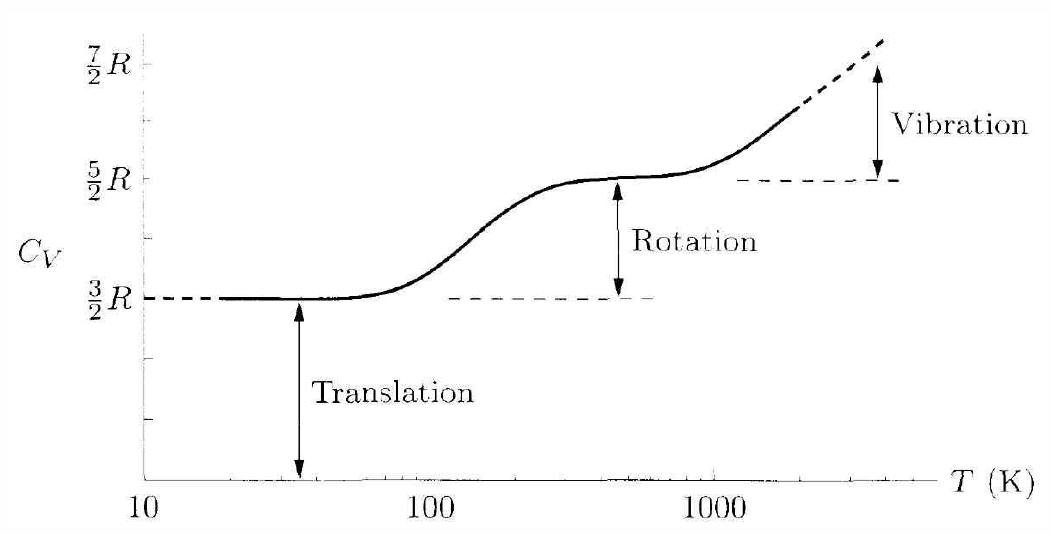
From the kinetic theory of gases, one can show that \[\begin{aligned} \hbox{monatomic gases:} \quad &c\ns_V=\frac{3}{2}R\quad,\quad c\ns_p=\frac{5}{2}R \quad,\quad \gamma=\frac{5}{3}\\ \hbox{diatomic gases:} \quad &c\ns_V=\frac{5}{2}R\quad,\quad c\ns_p=\frac{7}{2}R \quad,\quad \gamma=\frac{7}{5}\\ \hbox{polyatomic gases:} \quad &c\ns_V=3R\quad,\quad c\ns_p=4R\, \quad,\quad \gamma=\frac{4}{3}\ .\end{aligned}\]

Digression : kinetic theory of gases

We will conclude in general from noninteracting classical statistical mechanics that the specific heat of a substance is \(c\ns_v=\half f R\), where \(f\) is the number of phase space coordinates, per particle, for which there is a quadratic kinetic or potential energy function. For example, a point particle has three translational degrees of freedom, and the kinetic energy is a quadratic function of their conjugate momenta: \(H\ns_0=(p_x^2 + p_y^2 + p_z^2)/2m\). Thus, \(f=3\). Diatomic molecules have two additional rotational degrees of freedom – we don’t count rotations about the symmetry axis – and their conjugate momenta also appear quadratically in the kinetic energy, leading to \(f=5\). For polyatomic molecules, all three Euler angles and their conjugate momenta are in play, and \(f=6\).

[CVsolids] Molar heat capacities \(c_V\) for three solids. The solid curves correspond to the predictions of the Debye model, which we shall discuss later.

The reason that \(f=5\) for diatomic molecules rather than \(f=6\) is due to quantum mechanics. While translational eigenstates form a continuum, or are quantized in a box with \(\RDelta k\ns_\alpha=2\pi/L\ns_\alpha\) being very small, since the dimensions \(L\ns_\alpha\) are macroscopic, angular momentum, and hence rotational kinetic energy, is quantized. For rotations about a principal axis with very low moment of inertia \(I\), the corresponding energy scale \(\hbar^2/2I\) is very large, and a high temperature is required in order to thermally populate these states. Thus, degrees of freedom with a quantization energy on the order or greater than \(\ve\ns_0\) are ‘frozen out’ for temperatures \(T\ltwid \ve\ns_0/\kB\).

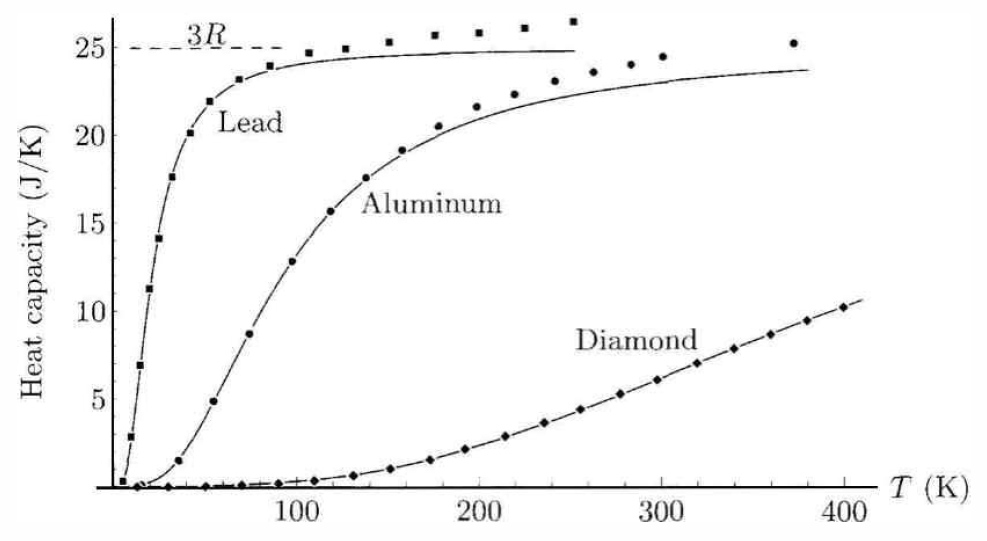
In solids, each atom is effectively connected to its neighbors by springs; such a potential arises from quantum mechanical and electrostatic consideration of the interacting atoms. Thus, each degree of freedom contributes to the potential energy, and its conjugate momentum contributes to the kinetic energy. This results in \(f=6\). Assuming only lattice vibrations, then, the high temperature limit for \(c\ns_V(T)\) for any solid is predicted to be \(3R=24.944\,\RJ/{mol}\,\RK\). This is called the Dulong-Petit law. The high temperature limit is reached above the so-called Debye temperature, which is roughly proportional to the melting temperature of the solid.

In table [cptab], we list \(c\ns_p\) and \({\tilde c}\ns_p\) for some common substances at \(T=25^\circ\,\)C (unless otherwise noted). Note that \(c\ns_p\) for the monatomic gases He and Ne is to high accuracy given by the value from kinetic theory, \(c\ns_p=\frac{5}{2}R=20.7864\,\RJ/{mol}\,\RK\). For the diatomic gases oxygen (\(\RO\ns_2\)) and air (mostly \(\RN\ns_2\) and \(\RO\ns_2\)), kinetic theory predicts \(c\ns_p=\frac{7}{2}R=29.10\), which is close to the measured values. Kinetic theory predicts \(c\ns_p=4R=33.258\) for polyatomic gases; the measured values for \(\RC\RO\ns_2\) and \(\RH\ns_2\RO\) are both about 10% higher.

Adiabatic transformations of ideal gases

Assuming \(dN=0\) and \(E=\nu\,\ve(T)\), Equation [QTVN] tells us that \[\dbar Q=C\ns_V\, dT + p\,dV\ .\] Invoking the ideal gas law to write \(p=\nu RT/V\), and remembering \(C\ns_V=\nu\, c\ns_V\), we have, setting \(\dbar Q=0\), \[{dT\over T} + {R\over c\ns_V}\,{dV\over V}=0\ .\] We can immediately integrate to obtain \[\dbar Q=0 \quad\Longrightarrow\quad\begin{cases} T V^{\gamma-1} = {constant} &\\ p V^\gamma = {constant} & \\ T^\gamma p^{1-\gamma} = {constant} & \end{cases}\] where the second two equations are obtained from the first by invoking the ideal gas law. These are all adiabatic equations of state. Note the difference between the adiabatic equation of state \(d(pV^\gamma)=0\) and the isothermal equation of state \(d(pV)=0\). Equivalently, we can write these three conditions as \[V^2\, T^f=V_0^2\, T_0^f\qquad,\qquad p^f \,V^{f+2}=p_0^f \,V_0^{f+2} \qquad,\qquad T^{f+2}\, p^{-2}=T_0^{f+2}\, p_0^{-2}\ .\]

It turns out that air is a rather poor conductor of heat. This suggests the following model for an adiabatic atmosphere. The hydrostatic pressure decrease associated with an increase \(dz\) in height is \(dp=-\vrh g\,dz\), where \(\vrh\) is the density and \(g\) the acceleration due to gravity. Assuming the gas is ideal, the density can be written as \(\vrh=Mp/RT\), where \(M\) is the molar mass. Thus, \[{dp\over p}=-{Mg\over RT}\,dz\ .\] If the height changes are adiabatic, then, from \(d(T^\gamma p^{1-\gamma})=0\), we have \[dT={\gamma-1\over\gamma}\,{T dp\over p}=-{\gamma-1\over\gamma}\,{Mg\over R}\,dz\ ,\] with the solution \[T(z)=T\ns_0-{\gamma-1\over\gamma}\,{Mg\over R}\,z= \bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)\,T\ns_0\ ,\] where \(T\ns_0=T(0)\) is the temperature at the earth’s surface, and \[\lambda={RT\ns_0\over Mg}\ .\] With \(M=28.88\,\Rg\) and \(\gamma=\frac{7}{5}\) for air, and assuming \(T\ns_0=293\,\RK\), we find \(\lambda=8.6\,\)km, and \(dT/dz=-(1-\gamma^{-1})\,T\ns_0/\lambda=-9.7\,\RK/{km}\). Note that in this model the atmosphere ends at a height \(z\ns_{max}=\gamma\lambda/(\gamma-1)=30\,\)km.

Again invoking the adiabatic equation of state, we can find \(p(z)\): \[{p(z)\over p\ns_0}=\bigg({T\over T\ns_0}\bigg)^{\gamma\over\gamma-1} = \bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)^{\gamma\over\gamma-1}\] Recall that \[e^x=\lim_{k\to\infty} \Big(1+{x\over k} \Big)^{\!k}\ .\] Thus, in the limit \(\gamma\to 1\), where \(k=\gamma/(\gamma-1)\to\infty\), we have \(p(z)=p\ns_0\,\exp(-z/\lambda)\). Finally, since \(\vrh\propto p/T\) from the ideal gas law, we have \[{\vrh(z)\over\vrh\ns_0}=\bigg(1-{\gamma-1\over\gamma}\,{z\over\lambda}\bigg)^{1\over\gamma-1}\ .\]

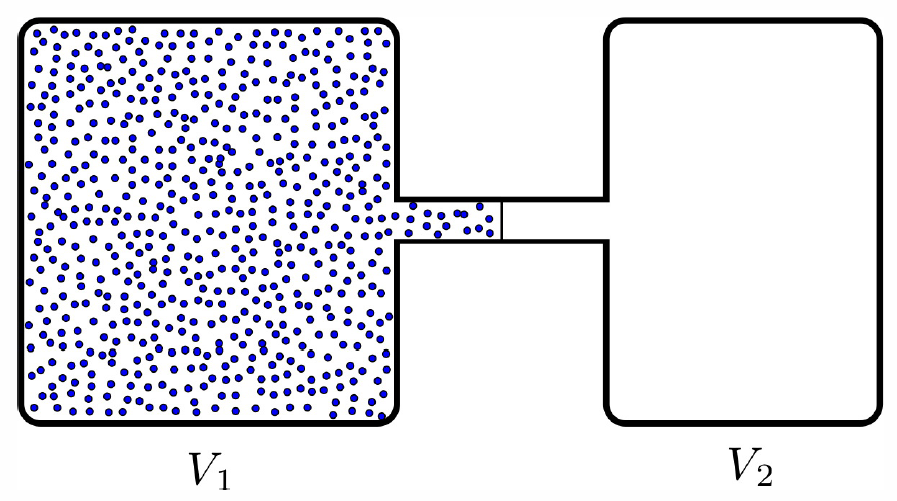
Adiabatic free expansion

Consider the situation depicted in Fig. [AFE]. A quantity (\(\nu\) moles) of gas in equilibrium at temperature \(T\) and volume \(V\ns_1\) is allowed to expand freely into an evacuated chamber of volume \(V\ns_2\) by the removal of a barrier. Clearly no work is done on or by the gas during this process, hence \(W=0\). If the walls are everywhere insulating, so that no heat can pass through them, then \(Q=0\) as well. The First Law then gives \(\RDelta E=Q-W=0\), and there is no change in energy.

If the gas is ideal, then since \(E(T,V,N)=N c\ns_V T\), then \(\RDelta E=0\) gives \(\RDelta T=0\), and there is no change in temperature. (If the walls are insulating against the passage of heat, they must also prevent the passage of particles, so \(\RDelta N=0\).) There is of course a change in volume: \(\RDelta V=V\ns_2\), hence there is a change in pressure. The initial pressure is \(p=N\kB T/V\ns_1\) and the final pressure is \(p'=N\kB T/ (V\ns_1+V\ns_2)\).

[AFE] In the adiabatic free expansion of a gas, there is volume expansion with no work or heat exchange with the environment: \(\RDelta E = Q = W = 0\).

If the gas is nonideal, then the temperature will in general change. Suppose \(E(T,V,N)=\alpha\, V^x\, N^{1-x}\, T^y\), where \(\alpha\), \(x\), and \(y\) are constants. This form is properly extensive: if \(V\) and \(N\) double, then \(E\) doubles. If the volume changes from \(V\) to \(V'\) under an adiabatic free expansion, then we must have, from \(\RDelta E=0\), \[\bigg({V\over V'}\bigg)^{\!x} = \bigg({T'\over T}\bigg)^{\!y} \qquad\Longrightarrow\qquad T'=T\cdot\bigg({V\over V'}\bigg)^{\!x/y}\ .\] If \(x/y>0\), the temperature decreases upon the expansion. If \(x/y<0\), the temperature increases. Without an equation of state, we can’t say precisely what happens to the pressure, although we know on general grounds that it must decrease because, as we shall see, thermodynamic stability entails a positive isothermal compressibility: \(\kappa\ns_T=-{1\over V}\big({\pz V\over\pz p}\big)\ns_{T,N}>0\) .

Adiabatic free expansion of a gas is a spontaneous process, arising due to the natural internal dynamics of the system. It is also irreversible. If we wish to take the gas back to its original state, we must do work on it to compress it. If the gas is ideal, then the initial and final temperatures are identical, so we can place the system in thermal contact with a reservoir at temperature \(T\) and follow a thermodynamic path along an isotherm. The work done on the gas during compression is then \[\CW=-N\kT\!\int\limits_{V\ns_\Rf}^{V\ns_\Ri}\!{dV\over V} =N\kT\,\ln\!\bigg({V\ns_\Rf\over V\ns_\Ri}\bigg) = N\kT\,\ln\!\bigg(\!1 + {V\ns_2\over V\ns_1}\bigg)\] The work done by the gas is \(W=\int\!p\, dV=-\CW\). During the compression, heat energy \(Q=W<0\) is transferred to the gas from the reservoir. Thus, \(\CQ=\CW>0\) is given off by the gas to its environment.