4.2: The Quantum Mechanical Trace
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/04:_Statistical_Ensembles/4.02:_The_Quantum_Mechanical_Trace), /content/body/p[1]/span, line 1, column 23
Thus far our understanding of ergodicity is rooted in the dynamics of classical mechanics. A Hamiltonian flow which is ergodic is one in which time averages can be replaced by phase space averages using the microcanonical ensemble. What happens, though, if our system is quantum mechanical, as all systems ultimately are?
The Density Matrix
First, let us consider that our system S will in general be in contact with a world W. We call the union of S and W the universe, U=W∪S. Let |N⟩ denote a quantum mechanical state of W, and let |n⟩ denote a quantum mechanical state of S. Then the most general wavefunction we can write is of the form
|Ψ⟩=∑N,nΨ†N,n|N⟩⊗|n⟩ .
Now let us compute the expectation value of some operator ˆA which acts as the identity within W, meaning ⟨N|ˆA|N′⟩=ˆAδ†NN′, where ˆA is the ‘reduced’ operator which acts within S alone. We then have
⟨Ψ|ˆA|Ψ⟩=∑N,N′∑n,n′Ψ∗N,nΨ∗N′,n′δ∗NN′⟨n|ˆA|n′⟩=Tr(ˆϱˆA) ,
where
ˆϱ=∑N†∑n†,n′Ψ∗N,nΨ∗N,n′|n′⟩⟨n|
is the density matrix. The time-dependence of ˆϱ is easily found:
ˆϱ(t)=∑N†∑n†,n′Ψ∗N,nΨ∗N,n′|n′(t)⟩⟨n(t)|=e−iˆHt/ℏˆϱe+iˆHt/ℏ ,
where ˆH is the Hamiltonian for the system S. Thus, we find
iℏ∂ˆϱ∂t=[ˆH,ˆϱ] .
Note that the density matrix evolves according to a slightly different equation than an operator in the Heisenberg picture, for which
ˆA(t)=e+iHt/ℏAe−iˆHt/ℏ⟹iℏ∂ˆA∂t=[ˆA,ˆH]=−[ˆH,ˆA] .

For Hamiltonian systems, we found that the phase space distribution ϱ(q,p,t) evolved according to the Liouville equation,
i∂ϱ∂t=Lϱ ,
where the Liouvillian L is the differential operator
L=−iNd∑j=1{∂ˆH∂p∗j∂∂q∗j−∂ˆH∂q∗j∂∂p∗j} .
Accordingly, any distribution ϱ(Λ∗1,…,Λ∗k) which is a function of constants of the motion Λ∗a(q,p) is a stationary solution to the Liouville equation: ∂∗tϱ(Λ∗1,…,Λ∗k)=0. Similarly, any quantum mechanical density matrix which commutes with the Hamiltonian is a stationary solution to Equation ???. The corresponding microcanonical distribution is
ˆϱ†E=δ(E−ˆH) .
Averaging the DOS
If our quantum mechanical system is placed in a finite volume, the energy levels will be discrete, rather than continuous, and the density of states (DOS) will be of the form
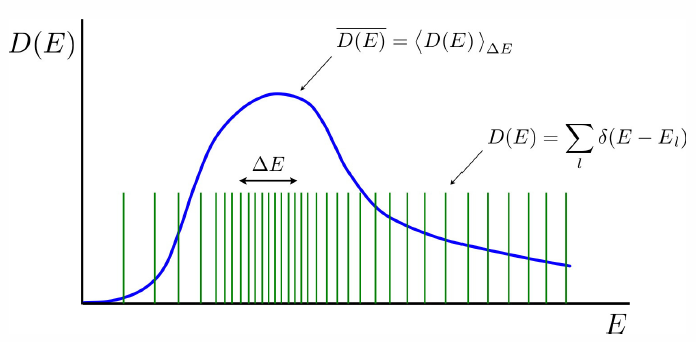
D(E)=Trδ(E−ˆH)=∑lδ(E−E∗l) ,
where {E∗l} are the eigenvalues of the Hamiltonian ˆH. In the thermodynamic limit, V→∞, and the discrete spectrum of kinetic energies remains discrete for all finite V but must approach the continuum result. To recover the continuum result, we average the DOS over a window of width ΔE:
¯D(E)=1ΔEE+ΔE∫EdE′D(E′) .
If we take the limit ΔE→0 but with ΔE≫δE, where δE is the spacing between successive quantized levels, we recover a smooth function, as shown in Figure 4.2.2. We will in general drop the bar and refer to this function as D(E). Note that δE∼1/D(E)=e−Nϕ(ε,v) is (typically) exponentially small in the size of the system, hence if we took ΔE∝V−1 which vanishes in the thermodynamic limit, there are still exponentially many energy levels within an interval of width ΔE.
Coherent States
The quantum-classical correspondence is elucidated with the use of coherent states. Recall that the one-dimensional harmonic oscillator Hamiltonian may be written
ˆH∗0=p22m+12mω20q2=ℏω∗0(a†a+12) ,
where a and a† are ladder operators satisfying [a,a†]=1, which can be taken to be
a=ℓ∂∂q+q2ℓ,a†=−ℓ∂∂q+q2ℓ ,
with ℓ=√ℏ/2mω∗0 . Note that
q=ℓ(a+a†),p=ℏ2iℓ(a−a†) .
The ground state satisfies aψ0(q)=0, which yields
ψ∗0(q)=(2πℓ2)−1/4e−q2/4ℓ2 .
The normalized coherent state |z⟩ is defined as
|z⟩=e−12|z|2eza†|0⟩=e−12|z|2∞∑n=0zn√n!|n⟩ .
The overlap of coherent states is given by
⟨z1|z2⟩=e−12|z†1|2e−12|z†2|2eˉz†1z†2 ,
hence different coherent states are not orthogonal. Despite this nonorthogonality, the coherent states allow a simple resolution of the identity,
1=∫d2z2πi|z⟩⟨z|;d2z2πi≡dRez dImzπ
which is straightforward to establish.
To gain some physical intuition about the coherent states, define
z≡Q2ℓ+iℓPℏ
and write |z⟩≡|Q,P⟩. One finds (exercise!)
ψ†Q,P(q)=⟨q|z⟩=(2πℓ2)−1/4e−iPQ/2ℏeiPq/ℏe−(q−Q)2/4ℓ2 ,
hence the coherent state ψ†Q,P(q) is a wavepacket Gaussianly localized about q=Q, but oscillating with average momentum P.
For example, we can compute
⟨Q,P|q|Q,P⟩=⟨z|ℓ(a+a†)|z⟩=2ℓRez=Q⟨Q,P|p|Q,P⟩=⟨z|ℏ2iℓ(a−a†)|z⟩=ℏℓImz=P
as well as
⟨Q,P|q2|Q,P⟩=⟨z|ℓ2(a+a†)2|z⟩=Q2+ℓ2⟨Q,P|p2|Q,P⟩=−⟨z|ℏ24ℓ2(a−a†)2|z⟩=P2+ℏ24ℓ2 .
Thus, the root mean square fluctuations in the coherent state |Q,P⟩ are
Δq=ℓ=√ℏ2mω∗0,Δp=ℏ2ℓ=√mℏω∗02,
and Δq⋅Δp=12ℏ. Thus we learn that the coherent state ψ∗Q,P(q) is localized in phase space, in both position and momentum. If we have a general operator ˆA(q,p), we can then write
⟨Q,P|ˆA(q,p)|Q,P⟩=A(Q,P)+O(ℏ) ,
where A(Q,P) is formed from ˆA(q,p) by replacing q→Q and p→P.
Since
d2z2πi≡dRez dImzπ=dQdP2πℏ ,
we can write the trace using coherent states as
TrˆA=12πℏ∞∫−∞dQ∞∫−∞dP⟨Q,P|ˆA|Q,P⟩ .
We now can understand the origin of the factor 2πℏ in the denominator of each (q†i,p†i) integral over classical phase space in Equation ???.
Note that ω∗0 is arbitrary in our discussion. By increasing ω∗0, the states become more localized in q and more plane wave like in p. However, so long as ω∗0 is finite, the width of the coherent state in each direction is proportional to ℏ1/2, and thus vanishes in the classical limit.


