6.1: Ising Model
( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand\Dalpha
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dbeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dgamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Ddelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Depsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarepsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dzeta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Deta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dtheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dvartheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Diota
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dkappa
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dlambda
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Dvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\DGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\DDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\DTheta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vmu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vnu
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vxi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vom
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarpi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarrho
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarsigma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vtau
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vupsilon
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vvarphi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vchi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vpsi
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\Vomega
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\VGamma
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\VDelta
Callstack:
at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\newcommand\BI{\mib I}}
\)
\newcommand { M}
\newcommand { m}
}
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
1$#1_$
\newcommand\SZ{\textsf Z}} \( \newcommand\kFd{k\ns_{\RF\dar}\)
\newcommand\mutB{\tilde\mu}\ns_\ssr{B}
\( \newcommand\xhihOZ
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
\( \newcommand\labar
Callstack:
at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
at template()
at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.01:_Ising_Model), /content/body/p/span, line 1, column 23
Definition
The simplest model of an interacting system consists of a lattice \CL of sites, each of which contains a spin \sigma\ns_i which may be either up (\sigma\ns_i=+1) or down (\sigma\ns_i=-1). The Hamiltonian is
\HH=-J\sum_{\langle ij\rangle} \sigma\ns_i \,\sigma\ns_j - \mu\ns_0 H\sum_i\sigma\ns_i\ .
When J>0, the preferred (lowest energy) configuration of neighboring spins is that they are aligned, \sigma\ns_i\,\sigma\ns_j=+1. The interaction is then called ferromagnetic. When J<0 the preference is for anti-alignment, \sigma\ns_i\,\sigma\ns_j=-1, which is antiferromagnetic.
This model is not exactly solvable in general. In one dimension, the solution is quite straightforward. In two dimensions, Onsager’s solution of the model (with H=0) is among the most celebrated results in statistical physics. In higher dimensions the system has been studied by numerical simulations (the Monte Carlo method) and by field theoretic calculations (renormalization group), but no exact solutions exist.
Ising Model in One Dimension
Consider a one-dimensional ring of N sites. The ordinary canonical partition function is then
\begin{split} Z\nd_{ring}&=\Tra e^{-\beta\HH}\\ &=\sum_{\{\sigma\ns_n\}}\prod_{n=1}^N e^{\beta J \sigma\ns_n\sigma\ns_{n+1}}\,e^{\beta\mu\ns_0 H\sigma\ns_n}\\ &=\Tra\! \big(R^N\big)\ , \end{split}
where \sigma\ns_{N+1}\equiv\sigma\ns_1 owing to periodic (ring) boundary conditions, and where R is a 2\times 2 transfer matrix,
\begin{split} R\ns_{\sigma\sigma'}&= e^{\beta J\sigma\sigma'}\,e^{\beta\mu\ns_0 H(\sigma+\sigma')/2}\\ &=\begin{pmatrix} e^{\beta J}\,e^{\beta\mu\ns_0 H} & e^{-\beta J} \\ e^{-\beta J} & e^{\beta J}\,e^{-\beta\mu\ns_0 H} \end{pmatrix}\\ &=e^{\beta J}\cosh(\beta\mu\nd_0 H) + e^{\beta J}\sinh(\beta\mu\ns_0 H)\,\tau^z + e^{-\beta J}\,\tau^x\ , \end{split}
where \tau^\alpha are the Pauli matrices. Since the trace of a matrix is invariant under a similarity transformation, we have
Z(T, H,N)=\lambda_+^N+ \lambda_-^N \ ,
where
\lambda\ns_\pm(T, H)=e^{\beta J}\cosh(\beta\mu\ns_0 H)\pm\sqrt{e^{2\beta J}\sinh^2(\beta\mu\ns_0 H) + e^{-2\beta J}}
are the eigenvalues of R. In the thermodynamic limit, N\to\infty, and the \lambda_+^N term dominates exponentially. We therefore have
F(T, H,N)=-N\kT\ln\lambda\ns_+(T, H)\ .
From the free energy, we can compute the magnetization,
M=-\pabc{F}{ H}{T,N}={N\mu\ns_0\,\sinh(\beta\mu\ns_0 H)\over\sqrt{\sinh^2(\beta\mu\ns_0 H) + e^{-4\beta J}}}
and the zero field isothermal susceptibility,
\xhi(T)={1\over N}\,{\pz M\over\pz H}\bigg|\nd_{ H=0}={\mu_0^2\over\kT}\,e^{2J/\kT}\ .
Note that in the noninteracting limit J\to 0 we recover the familiar result for a free spin. The effect of the interactions at low temperature is to vastly increase the susceptibility. Rather than a set of independent single spins, the system effectively behaves as if it were composed of large blocks of spins, where the block size \xi is the correlation length, to be derived below.
The physical properties of the system are often elucidated by evaluation of various correlation functions. In this case, we define
\begin{split} C(n)\equiv \blangle \sigma\ns_1\,\sigma\ns_{n+1}\brangle&={\Tra\big(\sigma\ns_1\,R\ns_{\sigma\ns_1\sigma\ns_2}\cdots R\ns_{\sigma\ns_n\sigma\ns_{n+1}}\,\sigma\ns_{n+1}\,R\ns_{\sigma\ns_{n+1}\sigma\ns_{n+2}}\cdots R\ns_{\sigma\ns_N\sigma\ns_1}\big) \over\Tra \big(R^N\big)}\\ &={\Tra\big(\Sigma\, R^n\, \Sigma\, R^{N-n}\big)\over \Tra \big(R^N\big)}\ , \end{split}
where 0<n<N, and where
\Sigma=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\ .
To compute this ratio, we decompose R in terms of its eigenvectors, writing
R=\lambda\ns_+\, \tket{+}\tbra{+} + \lambda\ns_-\, \tket{-}\tbra{-}\ .
Then
C(n)={\lambda_+^N\,\Sigma^2_{++} + \lambda_-^N\,\Sigma^2_{--} + \big(\lambda_+^{N-n}\,\lambda_-^n + \lambda_+^n\,\lambda_-^{N-n}\big)\,\Sigma\ns_{+-}\Sigma\ns_{-+}\over \lambda_+^N + \lambda_-^N}\ ,
where
\Sigma\ns_{\mu\mu'}=\sexpect{\mu}{\Sigma}{\mu'}\ .
Zero External Field
Consider the case H=0, where R=e^{\beta J} + e^{-\beta J}\,\tau^x, where \tau^x is the Pauli matrix. Then
\sket{\pm}=\frac{1}{\sqrt{2}}\Big(\tket{\!\uar} \pm \tket{\!\dar}\Big)\ ,
the eigenvectors of R are
\psi\nd_\pm={1\over\sqrt{2}}\begin{pmatrix} 1 \\ \pm 1 \end{pmatrix}\ , \label{evecs}
and \Sigma\ns_{++}=\Sigma\ns_{--}=0, while \Sigma\ns_{\pm}= \Sigma\ns_{-+}=1. The corresponding eigenvalues are
\lambda\ns_+=2\cosh(\beta J)\qquad,\qquad \lambda\ns_-=2\sinh(\beta J)\ .
The correlation function is then found to be
\begin{split} C(n)\equiv \blangle \sigma\ns_1\,\sigma\ns_{n+1}\brangle&= {\lambda_+^{N-|n|}\,\lambda_-^{|n|}+ \lambda_+^{|n|}\, \lambda_-^{N-|n|}\over\lambda_+^N + \lambda_-^N}\\ &={\tanh^{|n|}(\beta J) + \tanh^{N-|n|}(\beta J)\over 1+ \tanh^N(\beta J)}\bvph\\ &\approx \tanh^{|n|}(\beta J)\qquad (N\to\infty)\ . \end{split}
This result is also valid for n<0, provided |n|\le N. We see that we may write
C(n)=e^{-|n|/\xi(T)}\ ,
where the correlation length is
\xi(T)={1\over\ln{ctnh}(J/\kT)}\ .
Note that \xi(T) grows as T\to 0 as \xi\approx \half \,e^{2J/\kT}.
Chain with free ends
When the chain has free ends, there are (N\!-\!1) links, and the partition function is
\begin{split} Z\nd_{chain}&=\sum_{\sigma,\sigma'} \big( R^{N-1}\big)\nd_{\sigma\sigma'}\\ &=\sum_{\sigma,\sigma'}\Big\{\lambda_+^{N-1}\,\psi_+(\sigma)\,\psi_+(\sigma')+\lambda_-^{N-1}\,\psi_-(\sigma)\,\psi_-(\sigma')\Big\}\ , \end{split}
where \psi\nd_\pm(\sigma)=\sbraket{\sigma}{\pm}. When H=0, we make use of Equation \ref{evecs} to obtain
R^{N-1}={1\over 2} \begin{pmatrix} 1 &1 \\ 1 & 1 \end{pmatrix} \big(2\cosh\beta J\big)^{N-1} + {1\over 2} \begin{pmatrix} 1 & -1 \\ -1& 1 \end{pmatrix} \big(2\sinh\beta J\big)^{N-1} \ ,
and therefore
Z\nd_{chain}=2^N\cosh^{N-1}(\beta J)\ .
There’s a nifty trick to obtaining the partition function for the Ising chain which amounts to a change of variables. We define
\nu\nd_n\equiv\sigma\nd_n\,\sigma\nd_{n+1}\qquad (n=1\,,\,\ldots\,,\,N-1)\ .
Thus, \nu\nd_1=\sigma\nd_1\sigma\nd_2, \nu_2=\sigma\nd_2\sigma\nd_3, Note that each \nu\nd_j takes the values \pm 1. The Hamiltonian for the chain is
H\nd_{chain}=-J\sum_{n=1}^{N-1}\sigma\nd_n\,\sigma\nd_{n+1}=-J\sum_{n=1}^{N-1}\nu\nd_n\ .
The state of the system is defined by the N Ising variables \{\sigma\nd_1\,,\,\nu\nd_1\,,\,\ldots\,,\,\nu\nd_{N-1}\}. Note that \sigma\nd_1 doesn’t appear in the Hamiltonian. Thus, the interacting model is recast as N\!-\!1 noninteracting Ising spins, and the partition function is
\begin{split} Z\nd_{chain}&={Tr}\,e^{-\beta H\nd_{chain}}\\ &=\sum_{\sigma\ns_1}\sum_{\nu\ns_1}\cdots\sum_{\nu\ns_{N-1}} e^{\beta J\nu\nd_1} e^{\beta J\nu\nd_2}\cdots e^{\beta J\nu\nd_{N-1}}\\ &=\sum_{\sigma\ns_1}\left(\sum_\nu e^{\beta J\nu}\right)^{\!\!N-1}=2^N\cosh^{N-1}(\beta J)\ . \end{split}
Ising model in two dimensions: Peierls’ argument
We have just seen how in one dimension, the Ising model never achieves long-ranged spin order. That is, the spin-spin correlation function decays asymptotically as an exponential function of the distance with a correlation length \xi(T) which is finite for all >0. Only for T=0 does the correlation length diverge. At T=0, there are two ground states, \sket{\!\!\uar\uar\uar\uar\cdots\uar} and \sket{\!\!\dar\dar\dar\dar\cdots\dar}. To choose between these ground states, we can specify a boundary condition at the ends of our one-dimensional chain, where we demand that the spins are up. Equivalently, we can apply a magnetic field H of order 1/N, which vanishes in the thermodynamic limit, but which at zero temperature will select the ‘all up’ ground state. At finite temperature, there is always a finite probability for any consecutive pair of sites (n,n\!+\!1) to be in a high energy state, either \sket{\!\!\uar\dar} or \sket{\!\!\dar\uar}. Such a configuration is called a domain wall, and in one-dimensional systems domain walls live on individual links. Relative to the configurations \sket{\!\!\uar\uar} and \sket{\!\!\dar\dar}, a domain wall costs energy 2J. For a system with M=xN domain walls, the free energy is
\begin{split} F&=2MJ - \kT\ln{N\choose M}\\ &=N\cdot\Bigg\{2Jx + \kT\Big[ x\ln x + (1-x)\ln (1-x)\Big]\Bigg\}\ , \end{split}
Minimizing the free energy with respect to x, one finds x=1\big/\big(e^{2J/\kT}+1\big), so the equilibrium concentration of domain walls is finite, meaning there can be no long-ranged spin order. In one dimension, entropy wins and there is always a thermodynamically large number of domain walls in equilibrium. And since the correlation length for T>0 is finite, any boundary conditions imposed at spatial infinity will have no thermodynamic consequences since they will only be ‘felt’ over a finite range.
As we shall discuss in the following chapter, this consideration is true for any system with sufficiently short-ranged interactions and a discrete global symmetry. Another example is the q-state Potts model,
H=-J\sum_{\langle ij\rangle}\delta\nd_{\sigma\ns_i,\sigma\ns_j}-h\sum_i\delta\nd_{\sigma\ns_i,1}\ .
Here, the spin variables \sigma\ns_i take values in the set \{1,2,\ldots,q\} on each site. The equivalent of an external magnetic field in the Ising case is a field h which prefers a particular value of \sigma (\sigma=1 in the above Hamiltonian). See the appendix in §8 for a transfer matrix solution of the one-dimensional Potts model.
What about higher dimensions? A nifty argument due to R. Peierls shows that there will be a finite temperature phase transition for the Ising model on the square lattice1. Consider the Ising model, in zero magnetic field, on a N\ns_x\times N\ns_y square lattice, with N\ns_{x,y}\to \infty in the thermodynamic limit. Along the perimeter of the system we impose the boundary condition \sigma\ns_i=+1. Any configuration of the spins may then be represented uniquely in the following manner. Start with a configuration in which all spins are up. Next, draw a set of closed loops on the lattice. By definition, the loops cannot share any links along their boundaries, each link on the lattice is associated with at most one such loop. Now flip all the spins inside each loop from up to down. Identify each such loop configuration with a label \Gamma. The partition function is
Z=\Tra e^{-\beta\HH}=\sum_\Gamma e^{-2\beta J L\ns_\Gamma}\ ,
where L\ns_\Gamma is the total perimeter of the loop configuration \Gamma. The domain walls are now loops, rather than individual links, but as in the one-dimensional case, each link of each domain wall contributes an energy +2J relative to the ground state.
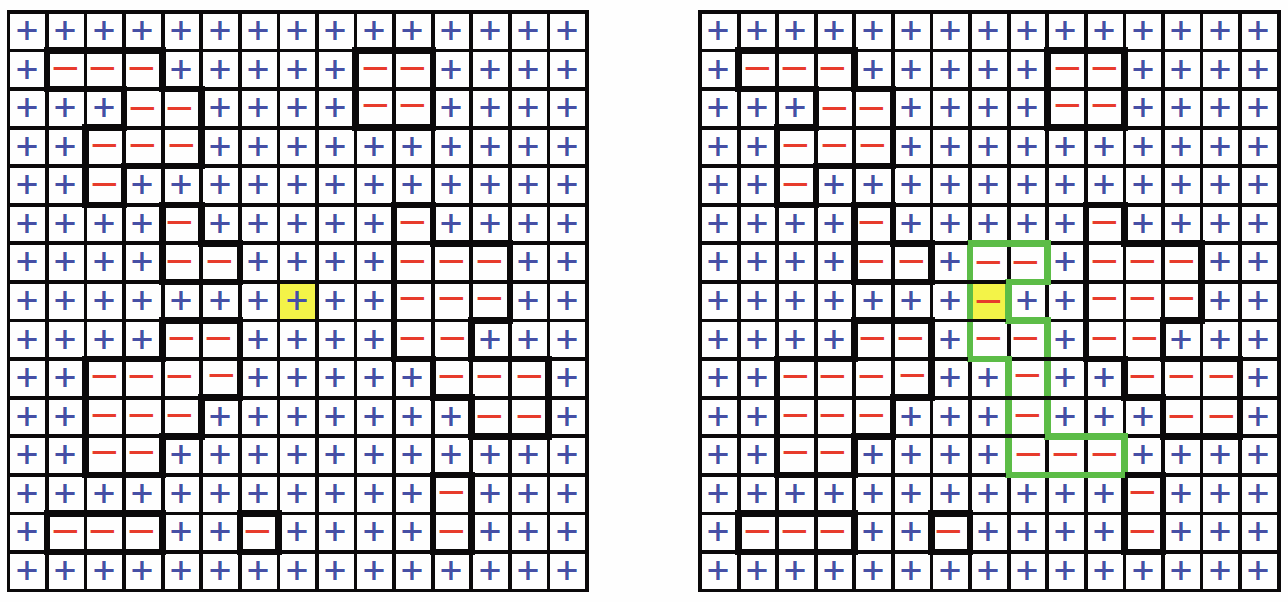
Now we wish to compute the average magnetization of the central site (assume N\ns_{x,y} are both odd, so there is a unique central site). This is given by the difference P\ns_+(0)-P\ns_-(0), where P\ns_\mu(0)= \blangle \delta\ns_{\sigma\ns_0\,,\,\mu}\brangle is the probability that the central spin has spin polarization \mu. If P\ns_+(0) > P\ns_-(0), then the magnetization per site m=P\ns_+(0)-P\ns_-(0) is finite in the thermodynamic limit, and the system is ordered. Clearly
P\ns_+(0)={1\over Z}\sum_{\Gamma \in \RSigma\ns_+} e^{-2\beta J L\ns_\Gamma}\ ,
where the restriction on the sum indicates that only those configurations where the central spin is up (\sigma\ns_0=+1) are to be included (Figure \PageIndex{1a}). Similarly,
P\ns_-(0)={1\over Z}\sum_{\widetilde\Gamma \in \RSigma\ns_-} e^{-2\beta J L\ns_{\widetilde\Gamma}}\ ,
where only configurations in which \sigma\ns_0=-1 are included in the sum. Here we have defined
\RSigma\ns_\pm=\Big\{ \Gamma\ \big|\ \sigma\ns_0=\pm \Big\}\ .
\RSigma\ns_+(\Sigma\ns_-) is the set of configurations \Gamma in which the central spin is always up (down). Consider now the construction in Figure \PageIndex{1b}. Any loop configuration {\widetilde\Gamma}\in\RSigma\ns_- may be associated with a unique loop configuration \Gamma\in\RSigma\ns_+ by reversing all the spins within the loop of {\widetilde\Gamma} which contains the origin. Note that the map from {\widetilde\Gamma} to \Gamma is many-to-one. That is, we can write {\widetilde\Gamma}=C\ns_\gamma\circ\Gamma, where C\ns_\gamma overturns the spins within the loop \gamma, with the conditions that (i) \gamma contains the origin, and (ii) none of the links in the perimeter of \gamma coincide with any of the links from the constituent loops of \Gamma. Let us denote this set of loops as \RUps\ns_{\!\Gamma}:
\RUps\ns_{\!\Gamma}=\Big\{ \gamma\ :\ \hbox{$0\in{int}(\gamma)$ and $\gamma\cap\Gamma=\emptyset$} \Big\}\ .
Then
m=P\ns_+(0)-P\ns_-(0)={1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} \bigg( 1 - \sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}}\bigg)\ .
If we can prove that \sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}}<1, then we will have established that m>0. Let us ask: how many loops \gamma are there in \Ups\ns_{\!\Gamma} with perimeter L? We cannot answer this question exactly, but we can derive a rigorous upper bound for this number, which, following Peliti, we call g(L). We claim that
g(L) < {2\over 3L}\cdot 3^L\cdot \bigg({L\over 4}\bigg)^{\!2} = {L\over 24}\cdot 3^L\ . \label{gupper}
To establish this bound, consider any site on such a loop \gamma. Initially we have 4 possible directions to proceed to the next site, but thereafter there are only 3 possibilities for each subsequent step, since the loop cannot run into itself. This gives 4\cdot 3^{L-1} possibilities. But we are clearly overcounting, since any point on the loop could have been chosen as the initial point, and moreover we could have started by proceeding either clockwise or counterclockwise. So we are justified in dividing this by 2L. We are still overcounting, because we have not accounted for the constraint that \gamma is a closed loop, nor that \gamma\cap\Gamma=\emptyset. We won’t bother trying to improve our estimate to account for these constraints. However, we are clearly undercounting due to the fact that a given loop can be translated in space so long as the origin remains within it. To account for this, we multiply by the area of a square of side length L/4, which is the maximum area that can be enclosed by a loop of perimeter L. We therefore arrive at Equation \ref{gupper}. Finally, we note that the smallest possible value of L is L=4, corresponding to a square enclosing the central site alone. Therefore
\sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}} < {1\over 12} \sum_{k=2}^\infty k\cdot \big(3\,e^{-2\beta J}\big)^{2k} = {x^4 \, (2-x^2)\over 12\,(1-x^2)^2}\equiv r\ , \label{roft}
where x=3\,e^{-2\beta J}. Note that we have accounted for the fact that the perimeter L of each loop \gamma must be an even integer. The sum is smaller than unity provided x < x\ns_0 = 0.869756 \ldots, hence the system is ordered provided
{\kT\over J} < {2\over \ln(3/x\ns_0)}=1.61531\ .
The exact result is \kB T\ns_\Rc=2J/\sinh^{-1}(1)=2.26918\ldots The Peierls argument has been generalized to higher dimensional lattices as well2.
With a little more work we can derive a bound for the magnetization. We have shown that
P\ns_-(0)={1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} \sum_{\gamma\in\RUps\ns_{\!\Gamma}} e^{-2\beta J L\ns_{\gamma}} < r\cdot {1\over Z}\sum_{\Gamma\in\RSigma\ns_+} e^{-2\beta J L\ns_\Gamma} = r\,P\ns_+(0)\ .
Thus,
1=P\ns_+(0)+P\ns_-(0) < (1+r) \, P\ns_+(0)
and therefore
m = P\ns_+(0) - P\ns_-(0) > (1-r) \, P\ns_+(0) > {1-r\over 1+r}\ ,
where r(T) is given in Equation \ref{roft}.
Two dimensions or one?
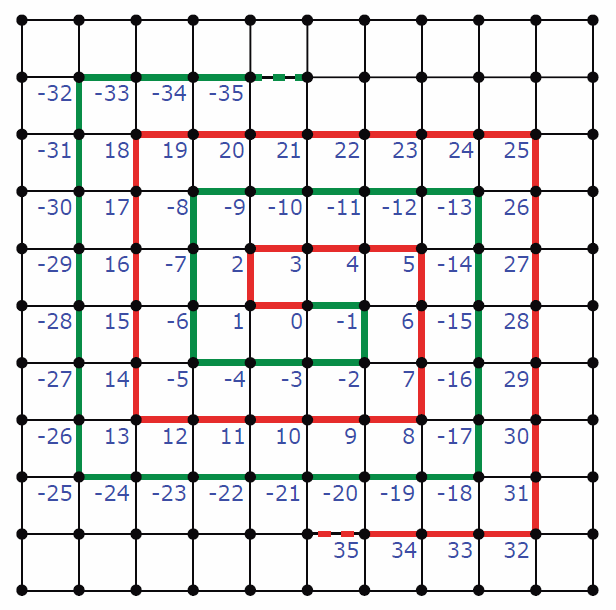
We showed that the one-dimensional Ising model has no finite temperature phase transition, and is disordered at any finite temperature T, but in two dimensions on the square lattice there is a finite critical temperature T\ns_\Rc below which there is long-ranged order. Consider now the construction depicted in Figure \PageIndex{2}, where the sites of a two-dimensional square lattice are mapped onto those of a linear chain3. Clearly we can elicit a one-to-one mapping between the sites of a two-dimensional square lattice and those of a one-dimensional chain. That is, the two-dimensional square lattice Ising model may be written as a one-dimensional Ising model,
\HH=-J\!\!\sum_{\langle ij\rangle}^{\ssr{square}\atop\ssr{lattice}}\!\!\sigma\ns_i \, \sigma\ns_j = -\!\!\sum_{n,n'}^{\ssr{linear}\atop\ssr{chain}} \!\! J\ns_{nn'}\,\sigma\ns_n \, \sigma\ns_{n'}\ .
How can this be consistent with the results we have just proven?
The fly in the ointment here is that the interaction along the chain J\ns_{n,n'} is long-ranged. This is apparent from inspecting the site labels in Figure \PageIndex{2}. Note that site n=15 is linked to sites n'=14 and n'=16, but also to sites n'=-6 and n'=-28. With each turn of the concentric spirals in the figure, the range of the interaction increases. To complicate matters further, the interactions are no longer translationally invariant, J\ns_{nn'}\ne J(n-n'). But it is the long-ranged nature of the interactions on our contrived one-dimensional chain which spoils our previous energy-entropy argument, because now the domain walls themselves interact via a long-ranged potential. Consider for example the linear chain with J\ns_{n,n'}=J\,|n-n'|^{-\alpha}, where \alpha > 0. Let us compute the energy of a domain wall configuration where \sigma\ns_n=+1 if n > 0 and \sigma\ns_n=-1 if n\le 0. The domain wall energy is then
\RDelta = \sum_{m=0}^\infty\sum_{n=1}^\infty {2J\over |m+n|^\alpha}\ .
Here we have written one of the sums in terms of m=-n'. For asymptotically large m and n, we can write \BR=(m,n) and we obtain an integral over the upper right quadrant of the plane:
\int\limits_1^\infty\!\!dR\> R\!\int\limits_0^{\pi/2}\!\!\!d\phi\>{2J\over R^\alpha \,(\cos\phi+\sin\phi)^\alpha}=2^{-\alpha/2}\!\!\!\! \int\limits_{-\pi/4}^{\pi/4}\!\!\!\!{d\phi\over\cos^\alpha\!\phi}\int\limits_1^\infty\!\!{dR\over R^{\alpha-1}}\ .
The \phi integral is convergent, but the R integral diverges for \alpha\le 2. For a finite system, the upper bound on the R integral becomes the system size L. For \alpha>2 the domain wall energy is finite in the thermodynamic limit L\to\infty. In this case, entropy again wins. the entropy associated with a single domain wall is \kB\ln L, and therefore F=E-\kT is always lowered by having a finite density of domain walls. For \alpha<2, the energy of a single domain wall scales as L^{2-\alpha}. It was first proven by F. J. Dyson in 1969 that this model has a finite temperature phase transition provided 1 < \alpha < 2. There is no transition for \alpha<1 or \alpha>2. The case \alpha=2 is special, and is discussed as a special case in the beautiful renormalization group analysis by J. M. Kosterlitz in Phys. Rev. Lett. 37, 1577 (1976).
High temperature expansion
Consider once again the ferromagnetic Ising model in zero field (H=0), but on an arbitrary lattice. The partition function is
Z=\Tra e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j} =\big(\!\cosh\beta J\big)^{N\ns_\ssr{L}}\Tra\Bigg\{\prod_{\langle ij\rangle} \big(1 + x\,\sigma\ns_i\,\sigma\ns_j\big)\Bigg\}\ , \label{HTEZ}
where x=\tanh\beta J and N\ns_\ssr{L} is the number of links. For regular lattices, N\ns_\ssr{L}=\half z N, where N is the number of lattice sites and z is the lattice coordination number, the number of nearest neighbors for each site. We have used
e^{\beta J\sigma\sigma'}=\cosh\beta J \cdot \Big\{ 1 + \sigma\sigma'\,\tanh\beta J\Big\}=\begin{cases} e^{+\beta J} & {if}\ \sigma\sigma'=+1 \\ e^{-\beta J} & {if}\ \sigma\sigma'=-1\ .\end{cases}
We expand Equation \ref{HTEZ} in powers of x, resulting in a sum of 2^{N\ns_\ssr{L}} terms, each of which can be represented graphically in terms of so-called lattice animals. A lattice animal is a distinct (including reflections and rotations) arrangement of adjacent plaquettes on a lattice. In order that the trace not vanish, only such configurations and their compositions are permitted. This is because each \sigma\ns_i for every given site i must occur an even number of times in order for a given term in the sum not to vanish. For all such terms, the trace is 2^N. Let \Gamma represent a collection of lattice animals, and g\ns_\Gamma the multiplicity of \Gamma. Then
Z=2^N\big(\!\cosh\beta J\big)^{N\ns_\ssr{L}}\sum_\Gamma g\ns_\Gamma \,\big(\!\tanh\beta J\big)^{L\ns_\Gamma}\ ,
where L\ns_\Gamma is the total number of sites in the diagram \Gamma, and g\ns_\Gamma is the multiplicity of \Gamma. Since x vanishes as T\to\infty, this procedure is known as the high temperature expansion (HTE).
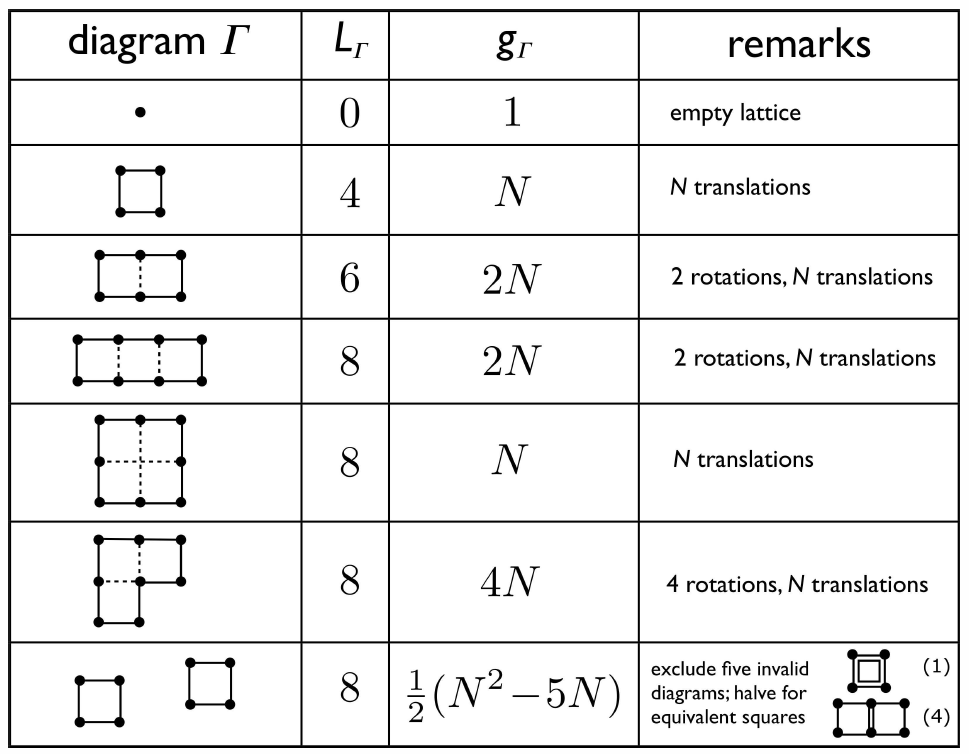
For the square lattice, he enumeration of all lattice animals with up to order eight is given in Figure \PageIndex{3}. For the diagram represented as a single elementary plaquette, there are N possible locations for the lower left vertex. For the 2\times 1 plaquette animal, one has g=2N, because there are two inequivalent orientations as well as N translations. For two disjoint elementary squares, one has g=\half N(N-5), which arises from subtracting 5N ‘illegal’ configurations involving double lines (remember each link in the partition sum appears only once!), shown in the figure, and finally dividing by two because the individual squares are identical. Note that N(N-5) is always even for any integer value of N. Thus, to lowest interesting order on the square lattice,
Z=2^N\big(\!\cosh\beta J\big)^{2N} \Big\{ 1 + Nx^4 + 2N x^6 + \big(7-\frac{5}{2}\big) N x^8 + \half N^2 x^8 + \CO(x^{10}) \Big\} \ .
The free energy is therefore
\begin{split} F&= -\kT\ln 2 + N\kT\ln(1-x^2) - N\kT \Big[ x^4 + 2\, x^6 + \frac{9}{2}\,x^8 + \CO(x^{10}) \Big]\\ &=N\kT\ln 2 - N\kT\Big\{ x^2 + \frac{3}{2}\, x^4 + \frac{7}{3}\, x^6 + \frac{19}{4}\,x^8 + \CO(x^{10})\Big\} , \end{split}
again with x=\tanh\beta J. Note that we’ve substituted \cosh^2\!\beta J = 1/(1-x^2) to write the final result as a power series in x. Notice that the \CO(N^2) factor in Z has cancelled upon taking the logarithm, so the free energy is properly extensive.
Note that the high temperature expansion for the one-dimensional Ising chain yields
Z\ns_{chain}(T,N)=2^N\cosh^{N-1}\!\beta J \qquad,\qquad Z\ns_{ring}(T,N)=2^N\cosh^N\!\beta J\ ,
in agreement with the transfer matrix calculations. In higher dimensions, where there is a finite temperature phase transition, one typically computes the specific heat c(T) and tries to extract its singular behavior in the vicinity of T\ns_\Rc, where c(T)\sim A\,(T-T\ns_\Rc)^{-\alpha}. Since x(T)=\tanh(J/\kT) is analytic in T, we have c(x)\sim A'\,(x-x\ns_\Rc)^{-\alpha}, where x\ns_\Rc=x(T\ns_\Rc). One assumes x\ns_\Rc is the singularity closest to the origin and corresponds to the radius of convergence of the high temperature expansion. If we write
c(x)=\sum_{n=0}^\infty a\ns_n\,x^n \sim A'' \bigg(1-{x\over x\ns_\Rc}\bigg)^{-\alpha}\ ,
then according to the binomial theorem we should expect
{a\ns_n\over a\ns_{n-1}}={1\over x\ns_\Rc}\bigg[1-{1-\alpha\over n}\bigg]\ .
Thus, by plotting a\ns_n/a\ns_{n-1} versus 1/n, one extracts 1/x\ns_\Rc as the intercept, and (\alpha-1)/x\ns_\Rc as the slope.
High temperature expansion for correlation functions
Can we also derive a high temperature expansion for the spin-spin correlation function C\ns_{kl}=\langle \sigma\ns_k \, \sigma\ns_l \rangle ? Yes we can. We have
C\ns_{kl}={\Tra\! \left[\sigma\ns_k\,\sigma\ns_l\,e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j}\right] \over \Tra\! \left[e^{\beta J \sum_{\langle ij\rangle}\sigma\ns_i\,\sigma\ns_j}\right] } \equiv {Y\ns_{kl}\over Z}\ .
Recall our analysis of the partition function Z. We concluded that in order for the trace not to vanish, the spin variable \sigma\ns_i on each site i must occur an even number of times in the expansion of the product. Similar considerations hold for Y\ns_{kl}, except now due to the presence of \sigma\ns_k and \sigma\ns_l, those variables now must occur an odd number of times when expanding the product. It is clear that the only nonvanishing diagrams will be those in which there is a finite string connecting sites k and l, in addition to the usual closed HTE loops. See Figure \PageIndex{4} for an instructive sketch. One then expands both Y\ns_{kl} as well as Z in powers of x=\tanh\beta J, taking the ratio to obtain the correlator C\ns_{kl}. At high temperatures (x\to 0), both numerator and denominator are dominated by the configurations \Gamma with the shortest possible total perimeter. For Z, this means the trivial path \Gamma=\{\emptyset\}, while for Y\ns_{kl} this means finding the shortest length path from k to l. (If there is no straight line path from k to l, there will in general be several such minimizing paths.) Note, however, that the presence of the string between sites k and l complicates the analysis of g\ns_\Gamma for the closed loops, since none of the links of \Gamma can intersect the string. It is worth stressing that this does not mean that the string and the closed loops cannot intersect at isolated sites, but only that they share no common links; see once again Figure \PageIndex{4}.