6.2: Nonideal Classical Gases

\( \newcommand\bes{\begin{equation}\begin{split}}\)
\( \newcommand\ltwid{\propto}\)
\( \newcommand\ees{\end{split}\end{equation}}\)
\( \newcommand\mib{\mathbf}\)
\( \newcommand\Sa{\textsf a}\)
\( \newcommand\Sb{\textsf b}\)
\( \newcommand\Sc{\textsf c}\)
\( \newcommand\Sd{\textsf d}\)
\( \newcommand\Se{\textsf e}\)
\( \newcommand\Sf{\textsf f}\)
\( \newcommand\Sg{\textsf g}\)
\( \newcommand\Sh{\textsf h}\)
\( \newcommand\Si{\textsf i}\)
\( \newcommand\Sj{\textsf j}\)
\( \newcommand\Sk{\textsf k}\)
\( \newcommand\Sl{\textsf l}\)
\( \newcommand\Sm{\textsf m}\)
\( \newcommand\Sn{\textsf n}\)
\( \newcommand\So{\textsf o}\)
\( \newcommand\Sp{\textsf p}\)
\( \newcommand\Sq{\textsf q}\)
\( \newcommand\Sr{\textsf r}\)
\( \newcommand\Ss{\textsf s}\)
\( \newcommand\St{\textsf t}\)
\( \newcommand\Su{\textsf u}\)
\( \newcommand\Sv{\textsf v}\)
\( \newcommand\Sw{\textsf w}\)
\( \newcommand\Sx{\textsf x}\)
\( \newcommand\Sy{\textsf y}\)
\( \newcommand\Sz{\textsf z}\)
\( \newcommand\SA{\textsf A}\)
\( \newcommand\SB{\textsf B}\)
\( \newcommand\SC{\textsf C}\)
\( \newcommand\SD{\textsf D}\)
\( \newcommand\SE{\textsf E}\)
\( \newcommand\SF{\textsf F}\)
\( \newcommand\SG{\textsf G}\)
\( \newcommand\SH{\textsf H}\)
\( \newcommand\SI{\textsf I}\)
\( \newcommand\SJ{\textsf J}\)
\( \newcommand\SK{\textsf K}\)
\( \newcommand\SL{\textsf L}\)
\( \newcommand\SM{\textsf M}\)
\( \newcommand\SN{\textsf N}\)
\( \newcommand\SO{\textsf O}\)
\( \newcommand\SP{\textsf P}\)
\( \newcommand\SQ{\textsf Q}\)
\( \newcommand\SR{\textsf R}\)
\( \newcommand\SS{\textsf S}\)
\( \newcommand\ST{\textsf T}\)
\( \newcommand\SU{\textsf U}\)
\( \newcommand\SV{\textsf V}\)
\( \newcommand\SW{\textsf W}\)
\( \newcommand\SX{\textsf X}\)
\( \newcommand\SY{\textsf Y}\)
\( \newcommand\SZ{\textsf Z}\)
\( \newcommand\Ha{\hat a}\)
\( \newcommand\Hb{\hat b}\)
\( \newcommand\Hc{\hat c}\)
\( \newcommand\Hd{\hat d}\)
\( \newcommand\He{\hat e}\)
\( \newcommand\Hf{\hat f}\)
\( \newcommand\Hg{\hat g}\)
\( \newcommand\Hh{\hat h}\)
\( \newcommand\Hi{\hat \imath}\)
\( \newcommand\Hj{\hat \jmath}\)
\( \newcommand\Hk{\hat k}\)
\( \newcommand\Hl{\hat l}\)
\( \newcommand\Hm{\hat m}\)
\( \newcommand\Hn{\hat n}\)
\( \newcommand\Ho{\hat o}\)
\( \newcommand\Hp{\hat p}\)
\( \newcommand\Hq{\hat q}\)
\( \newcommand\Hr{\hat r}\)
\( \newcommand\Hs{\hat s}\)
\( \newcommand\Ht{\hat t}\)
\( \newcommand\Hu{\hat u}\)
\( \newcommand\Hv{\hat v}\)
\( \newcommand\Hw{\hat w}\)
\( \newcommand\Hx{\hat x}\)
\( \newcommand\Hy{\hat y}\)
\( \newcommand\Hz{\hat z}\)
\( \newcommand\HA{\hat A}\)
\( \newcommand\HB{\hat B}\)
\( \newcommand\HC{\hat C}\)
\( \newcommand\HD{\hat D}\)
\( \newcommand\HE{\hat E}\)
\( \newcommand\HF{\hat F}\)
\( \newcommand\HG{\hat G}\)
\( \newcommand\HH{\hat H}\)
\( \newcommand\HI{\hat I}\)
\( \newcommand\HJ{\hat J}\)
\( \newcommand\HK{\hat K}\)
\( \newcommand\HL{\hat L}\)
\( \newcommand\HM{\hat M}\)
\( \newcommand\HN{\hat N}\)
\( \newcommand\HO{\hat O}\)
\( \newcommand\HP{\hat P}\)
\( \newcommand\HQ{\hat Q}\)
\( \newcommand\HR{\hat R}\)
\( \newcommand\HS{\hat S}\)
\( \newcommand\HT{\hat T}\)
\( \newcommand\HU{\hat U}\)
\( \newcommand\HV{\hat V}\)
\( \newcommand\HW{\hat W}\)
\( \newcommand\HX{\hat X}\)
\( \newcommand\HY{\hat Y}\)
\( \newcommand\HZ{\hat Z}\)
\( \newcommand\Halpha{\hat\alpha}\)
\( \newcommand\Hbeta{\hat\beta}\)
\( \newcommand\Hgamma{\hat\gamma}\)
\( \newcommand\Hdelta{\hat\delta}\)
\( \newcommand\Hepsilon{\hat\epsilon}\)
\( \newcommand\Hvarepsilon{\hat\varepsilon}\)
\( \newcommand\Hzeta{\hat\zeta}\)
\( \newcommand\Heta{\hat\eta}\)
\( \newcommand\Htheta{\hat\theta}\)
\( \newcommand\Hvartheta{\hat\vartheta}\)
\( \newcommand\Hiota{\hat\iota}\)
\( \newcommand\Hkappa{\hat\kappa}\)
\( \newcommand\Hlambda{\hat\lambda}\)
\( \newcommand\Hmu{\hat\mu}\)
\( \newcommand\Hnu{\hat\nu}\)
\( \newcommand\Hxi{\hat\xi}\)
\( \newcommand\Hom{\hat\omicron}\)
\( \newcommand\Hpi{\hat\pi}\)
\( \newcommand\Hvarpi{\hat\varpi}\)
\( \newcommand\Hrho{\hat\rho}\)
\( \newcommand\Hvarrho{\hat\varrho}\)
\( \newcommand\Hsigma{\hat\sigma}\)
\( \newcommand\Hvarsigma{\hat\varsigma}\)
\( \newcommand\Htau{\var\tau}\)
\( \newcommand\Hupsilon{\hat\upsilon}\)
\( \newcommand\Hphi{\hat\phi}\)
\( \newcommand\Hvarphi{\hat\varphi}\)
\( \newcommand\Hchi{\hat\chi}\)
\( \newcommand\Hxhi{\hat\xhi}\)
\( \newcommand\Hpsi{\hat\psi}\)
\( \newcommand\Homega{\hat\omega}\)
\( \newcommand\HGamma{\hat\Gamma}\)
\( \newcommand\HDelta{\hat\Delta}\)
\( \newcommand\HTheta{\hat\Theta}\)
\( \newcommand\HLambda{\hat\Lambda}\)
\( \newcommand\HXi{\hat\Xi}\)
\( \newcommand\HPi{\hat\Pi}\)
\( \newcommand\HSigma{\hat\Sigma}\)
\( \newcommand\HUps{\hat\Upsilon}\)
\( \newcommand\HPhi{\hat\Phi}\)
\( \newcommand\HPsi{\hat\Psi}\)
\( \newcommand\HOmega{\hat\Omega}\)
\( \newcommand\xhat{\hat\Bx}\)
\( \newcommand\yhat{\hat\By}\)
\( \newcommand\zhat{\hat\Bz}\)
\( \newcommand\ehat{\hat\Be}\)
\( \newcommand\khat{\hat\Bk}\)
\( \newcommand\nhat{\hat\Bn}\)
\( \newcommand\rhat{\hat\Br}\)
\( \newcommand\phihat{\hat\Bphi}\)
\( \newcommand\thetahat{\hat\Btheta}\)
\( \newcommand\MA{\mathbb A}\)
\( \newcommand\MB{\mathbb B}\)
\( \newcommand\MC{\mathbb C}\)
\( \newcommand\MD{\mathbb D}\)
\( \newcommand\ME{\mathbb E}\)
\( \newcommand\MF{\mathbb F}\)
\( \newcommand\MG{\mathbb G}\)
\( \newcommand\MH{\mathbb H}\)
\( \newcommand\MI{\mathbb I}\)
\( \newcommand\MJ{\mathbb J}\)
\( \newcommand\MK{\mathbb K}\)
\( \newcommand\ML{\mathbb L}\)
\( \newcommand\MM{\mathbb M}\)
\( \newcommand\MN{\mathbb N}\)
\( \newcommand\MO{\mathbb O}\)
\( \newcommand\MP{\mathbb P}\)
\( \newcommand\MQ{\mathbb Q}\)
\( \newcommand\MR{\mathbb R}\)
\( \newcommand\MS{\mathbb S}\)
\( \newcommand\MT{\mathbb T}\)
\( \newcommand\MU{\mathbb U}\)
\( \newcommand\MV{\mathbb V}\)
\( \newcommand\MW{\mathbb W}\)
\( \newcommand\MX{\mathbb X}\)
\( \newcommand\MY{\mathbb Y}\)
\( \newcommand\MZ{\mathbb Z}\)
\( \newcommand\CA{\mathcal A}\)
\( \newcommand\CB{\mathcal B}\)
\( \newcommand\CC{\mathcal C}\)
\( \newcommand\CD{\mathcal D}\)
\( \newcommand\CE{\mathcal E}\)
\( \newcommand\CF{\mathcal F}\)
\( \newcommand\CG{\mathcal G}\)
\( \newcommand\CH{\mathcal H}\)
\( \newcommand\CI{\mathcal I}\)
\( \newcommand\CJ{\mathcal J}\)
\( \newcommand\CK{\mathcal K}\)
\( \newcommand\CL{\mathcal L}\)
\( \newcommand\CM{\mathcal M}\)
\( \newcommand\CN{\mathcal N}\)
\( \newcommand\CO{\mathcal O}\)
\( \newcommand\CP{\mathcal P}\)
\( \newcommand\CQ{\mathcal Q}\)
\( \newcommand\CR{\mathcal R}\)
\( \newcommand\CS{\mathcal S}\)
\( \newcommand\CT{\mathcal T}\)
\( \newcommand\CU{\mathcal U}\)
\( \newcommand\CV{\mathcal V}\)
\( \newcommand\CW{\mathcal W}\)
\( \newcommand\CX{\mathcal X}\)
\( \newcommand\CY{\mathcal Y}\)
\( \newcommand\CZ{\mathcal Z}\)
\( \newcommand\Fa{\mathfrak a}\)
\( \newcommand\Fb{\mathfrak b}\)
\( \newcommand\Fc{\mathfrak c}\)
\( \newcommand\Fd{\mathfrak d}\)
\( \newcommand\Fe{\mathfrak e}\)
\( \newcommand\Ff{\mathfrak f}\)
\( \newcommand\Fg{\mathfrak g}\)
\( \newcommand\Fh{\mathfrak h}\)
\( \newcommand\Fi{\mathfrak i}\)
\( \newcommand\Fj{\mathfrak j}\)
\( \newcommand\Fk{\mathfrak k}\)
\( \newcommand\Fl{\mathfrak l}\)
\( \newcommand\Fm{\mathfrak m}\)
\( \newcommand\Fn{\mathfrak n}\)
\( \newcommand\Fo{\mathfrak o}\)
\( \newcommand\Fp{\mathfrak p}\)
\( \newcommand\Fq{\mathfrak q}\)
\( \newcommand\Fr{\mathfrak r}\)
\( \newcommand\Fs{\mathfrak s}\)
\( \newcommand\Ft{\mathfrak t}\)
\( \newcommand\Fu{\mathfrak u}\)
\( \newcommand\Fv{\mathfrak v}\)
\( \newcommand\Fw{\mathfrak w}\)
\( \newcommand\Fx{\mathfrak x}\)
\( \newcommand\Fy{\mathfrak y}\)
\( \newcommand\Fz{\mathfrak z}\)
\( \newcommand\FA{\mathfrak A}\)
\( \newcommand\FB{\mathfrak B}\)
\( \newcommand\FC{\mathfrak C}\)
\( \newcommand\FD{\mathfrak D}\)
\( \newcommand\FE{\mathfrak E}\)
\( \newcommand\FF{\mathfrak F}\)
\( \newcommand\FG{\mathfrak G}\)
\( \newcommand\FH{\mathfrak H}\)
\( \newcommand\FI{\mathfrak I}\)
\( \newcommand\FJ{\mathfrak J}\)
\( \newcommand\FK{\mathfrak K}\)
\( \newcommand\FL{\mathfrak L}\)
\( \newcommand\FM{\mathfrak M}\)
\( \newcommand\FN{\mathfrak N}\)
\( \newcommand\FO{\mathfrak O}\)
\( \newcommand\FP{\mathfrak P}\)
\( \newcommand\FQ{\mathfrak Q}\)
\( \newcommand\FR{\mathfrak R}\)
\( \newcommand\FS{\mathfrak S}\)
\( \newcommand\FT{\mathfrak T}\)
\( \newcommand\FU{\mathfrak U}\)
\( \newcommand\FV{\mathfrak V}\)
\( \newcommand\FW{\mathfrak W}\)
\( \newcommand\FX{\mathfrak X}\)
\( \newcommand\FY{\mathfrak Y}\)
\( \newcommand\FZ{\mathfrak Z}\)
\( \newcommand\Da{\dot a}\)
\( \newcommand\Db{\dot b}\)
\( \newcommand\Dc{\dot c}\)
\( \newcommand\Dd{\dot d}\)
\( \newcommand\De{\dot e}\)
\( \newcommand\Df{\dot f}\)
\( \newcommand\Dg{\dot g}\)
\( \newcommand\Dh{\dot h}\)
\( \newcommand\Di{\dot \imath}\)
\( \newcommand\Dj{\dot \jmath}\)
\( \newcommand\Dk{\dot k}\)
\( \newcommand\Dl{\dot l}\)
\( \newcommand\Dm{\dot m}\)
\( \newcommand\Dn{\dot n}\)
\( \newcommand\Do{\dot o}\)
\( \newcommand\Dp{\dot p}\)
\( \newcommand\Dq{\dot q}\)
\( \newcommand\Dr{\dot r}\)
\( \newcommand\Ds{\dot s}\)
\( \newcommand\Dt{\dot t}\)
\( \newcommand\Du{\dot u}\)
\( \newcommand\Dv{\dot v}\)
\( \newcommand\Dw{\dot w}\)
\( \newcommand\Dx{\dot x}\)
\( \newcommand\Dy{\dot y}\)
\( \newcommand\Dz{\dot z}\)
\( \newcommand\DA{\dot A}\)
\( \newcommand\DB{\dot B}\)
\( \newcommand\DC{\dot C}\)
\( \newcommand\DD{\dot D}\)
\( \newcommand\DE{\dot E}\)
\( \newcommand\DF{\dot F}\)
\( \newcommand\DG{\dot G}\)
\( \newcommand\DH{\dot H}\)
\( \newcommand\DI{\dot I}\)
\( \newcommand\DJ{\dot J}\)
\( \newcommand\DK{\dot K}\)
\( \newcommand\DL{\dot L}\)
\( \newcommand\DM{\dot M}\)
\( \newcommand\DN{\dot N}\)
\( \newcommand\DO{\dot O}\)
\( \newcommand\DP{\dot P}\)
\( \newcommand\DQ{\dot Q}\)
\( \newcommand\DR{\dot R}\)
\( \newcommand\DS{\dot S}\)
\( \newcommand\DT{\dot T}\)
\( \newcommand\DU{\dot U}\)
\( \newcommand\DV{\dot V}\)
\( \newcommand\DW{\dot W}\)
\( \newcommand\DX{\dot X}\)
\( \newcommand\DY{\dot Y}\)
\( \newcommand\DZ{\dot Z}\)
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Dmu{\dot\mu}\)
\( \newcommand\Dnu{\dot\nu}\)
\( \newcommand\Dxi{\dot\xi}\)
\( \newcommand\Dom{\dot\omicron}\)
\( \newcommand\Dpi{\dot\pi}\)
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Drho{\dot\rho}\)
\( \newcommand\Dvarrho{\dot\varrho}\)
\( \newcommand\Dsigma{\dot\sigma}\)
\( \newcommand\Dvarsigma{\dot\varsigma}\)
\( \newcommand\Dtau{\var\tau}\)
\( \newcommand\Dupsilon{\dot\upsilon}\)
\( \newcommand\Dphi{\dot\phi}\)
\( \newcommand\Dvarphi{\dot\varphi}\)
\( \newcommand\Dchi{\dot\chi}\)
\( \newcommand\Dpsi{\dot\psi}\)
\( \newcommand\Domega{\dot\omega}\)
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\DLambda{\dot\Lambda}\)
\( \newcommand\DXi{\dot\Xi}\)
\( \newcommand\DPi{\dot\Pi}\)
\( \newcommand\DSigma{\dot\Sigma}\)
\( \newcommand\DUps{\dot\Upsilon}\)
\( \newcommand\DPhi{\dot\Phi}\)
\( \newcommand\DPsi{\dot\Psi}\)
\( \newcommand\DOmega{\dot\Omega}\)
\( \newcommand\Va{\vec a}\)
\( \newcommand\Vb{\vec b}\)
\( \newcommand\Vc{\vec c}\)
\( \newcommand\Vd{\vec d}\)
\( \newcommand\Ve{\vec e}\)
\( \newcommand\Vf{\vec f}\)
\( \newcommand\Vg{\vec g}\)
\( \newcommand\Vh{\vec h}\)
\( \newcommand\Vi{\vec \imath}\)
\( \newcommand\Vj{\vec \jmath}\)
\( \newcommand\Vk{\vec k}\)
\( \newcommand\Vl{\vec l}\)
\( \newcommand\Vm{\vec m}\)
\( \newcommand\Vn{\vec n}\)
\( \newcommand\Vo{\vec o}\)
\( \newcommand\Vp{\vec p}\)
\( \newcommand\Vq{\vec q}\)
\( \newcommand\Vr{\vec r}\)
\( \newcommand\Vs{\vec s}\)
\( \newcommand\Vt{\vec t}\)
\( \newcommand\Vu{\vec u}\)
\( \newcommand\Vv{\vec v}\)
\( \newcommand\Vw{\vec w}\)
\( \newcommand\Vx{\vec x}\)
\( \newcommand\Vy{\vec y}\)
\( \newcommand\Vz{\vec z}\)
\( \newcommand\VA{\vec A}\)
\( \newcommand\VB{\vec B}\)
\( \newcommand\VC{\vec C}\)
\( \newcommand\VD{\vec D}\)
\( \newcommand\VE{\vec E}\)
\( \newcommand\VF{\vec F}\)
\( \newcommand\VG{\vec G}\)
\( \newcommand\VH{\vec H}\)
\( \newcommand\VI{\vec I}\)
\( \newcommand\VJ{\vec J}\)
\( \newcommand\VK{\vec K}\)
\( \newcommand\VL{\vec L}\)
\( \newcommand\VM{\vec M}\)
\( \newcommand\VN{\vec N}\)
\( \newcommand\VO{\vec O}\)
\( \newcommand\VP{\vec P}\)
\( \newcommand\VQ{\vec Q}\)
\( \newcommand\VR{\vec R}\)
\( \newcommand\VS{\vec S}\)
\( \newcommand\VT{\vec T}\)
\( \newcommand\VU{\vec U}\)
\( \newcommand\VV{\vec V}\)
\( \newcommand\VW{\vec W}\)
\( \newcommand\VX{\vec X}\)
\( \newcommand\VY{\vec Y}\)
\( \newcommand\VZ{\vec Z}\)
\( \newcommand\Valpha{\vec\alpha}\)
\( \newcommand\Vbeta{\vec\beta}\)
\( \newcommand\Vgamma{\vec\gamma}\)
\( \newcommand\Vdelta{\vec\delta}\)
\( \newcommand\Vepsilon{\vec\epsilon}\)
\( \newcommand\Vvarepsilon{\vec\varepsilon}\)
\( \newcommand\Vzeta{\vec\zeta}\)
\( \newcommand\Veta{\vec\eta}\)
\( \newcommand\Vtheta{\vec\theta}\)
\( \newcommand\Vvartheta{\vec\vartheta}\)
\( \newcommand\Viota{\vec\iota}\)
\( \newcommand\Vkappa{\vec\kappa}\)
\( \newcommand\Vlambda{\vec\lambda}\)
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\VTheta{\vec\Theta}\)
\( \newcommand\VLambda{\vec\Lambda}\)
\( \newcommand\VXi{\vec\Xi}\)
\( \newcommand\VPi{\vec\Pi}\)
\( \newcommand\VSigma{\vec\Sigma}\)
\( \newcommand\VUps{\vec\Upsilon}\)
\( \newcommand\VPhi{\vec\Phi}\)
\( \newcommand\VPsi{\vec\Psi}\)
\( \newcommand\VOmega{\vec\Omega}\)
\( \newcommand\BA{\mib A}\)
\( \newcommand\BB{\mib B}\)
\( \newcommand\BC{\mib C}\)
\( \newcommand\BD{\mib D}\)
\( \newcommand\BE{\mib E}\)
\( \newcommand\BF{\mib F}\)
\( \newcommand\BG{\mib G}\)
\( \newcommand\BH{\mib H}\)
\( \newcommand\BI{\mib I}}\)
\( \newcommand\BJ{\mib J}\)
\( \newcommand\BK{\mib K}\)
\( \newcommand\BL{\mib L}\)
\( \newcommand\BM{\mib M}\)
\( \newcommand\BN{\mib N}\)
\( \newcommand\BO{\mib O}\)
\( \newcommand\BP{\mib P}\)
\( \newcommand\BQ{\mib Q}\)
\( \newcommand\BR{\mib R}\)
\( \newcommand\BS{\mib S}\)
\( \newcommand\BT{\mib T}\)
\( \newcommand\BU{\mib U}\)
\( \newcommand\BV{\mib V}\)
\( \newcommand\BW{\mib W}\)
\( \newcommand\BX{\mib X}\)
\( \newcommand\BY{\mib Y}\)
\( \newcommand\BZ{\mib Z}\)
\( \newcommand\Ba{\mib a}\)
\( \newcommand\Bb{\mib b}\)
\( \newcommand\Bc{\mib c}\)
\( \newcommand\Bd{\mib d}\)
\( \newcommand\Be{\mib e}\)
\( \newcommand\Bf{\mib f}\)
\( \newcommand\Bg{\mib g}\)
\( \newcommand\Bh{\mib h}\)
\( \newcommand\Bi{\mib i}\)
\( \newcommand\Bj{\mib j}\)
\( \newcommand\Bk{\mib k}\)
\( \newcommand\Bl{\mib l}\)
\( \newcommand\Bm{\mib m}\)
\( \newcommand\Bn{\mib n}\)
\( \newcommand\Bo{\mib o}\)
\( \newcommand\Bp{\mib p}\)
\( \newcommand\Bq{\mib q}\)
\( \newcommand\Br{\mib r}\)
\( \newcommand\Bs{\mib s}\)
\( \newcommand\Bt{\mib t}\)
\( \newcommand\Bu{\mib u}\)
\( \newcommand\Bv{\mib v}\)
\( \newcommand\Bw{\mib w}\)
\( \newcommand\Bx{\mib x}\)
\( \newcommand\By{\mib y}\)
\( \newcommand\Bz{\mib z}\)\)
\( \newcommand\vrh{\varrho}\)
\( \newcommand\vsig{\varsigma}\)
\( \newcommand\ups{\upsilon}\)
\( \newcommand\eps{\epsilon}\)
\( \newcommand\ve{\varepsilon}\)
\( \newcommand\vth{\vartheta}\)
\( \newcommand\vphi{\varphi}\)
\( \newcommand\xhi{\chi}\)
\( \newcommand\Ups{\Upsilon}\)
\( \newcommand\Balpha{\mib\alpha}\)
\( \newcommand\Bbeta{\mib\beta}\)
\( \newcommand\Bgamma{\mib\gamma}\)
\( \newcommand\Bdelta{\mib\delta}\)
\( \newcommand\Beps{\mib\epsilon}\)
\( \newcommand\Bve{\mib\varepsilon}\)
\( \newcommand\Bzeta{\mib\zeta}\)
\( \newcommand\Beta{\mib\eta}\)
\( \newcommand\Btheta{\mib\theta}\)
\( \newcommand\Bvth{\mib\vartheta}\)
\( \newcommand\Biota{\mib\iota}\)
\( \newcommand\Bkappa{\mib\kappa}\)
\( \newcommand\Blambda{\mib\lambda}\)
\( \newcommand\Bmu{\mib\mu}\)
\( \newcommand\Bnu{\mib\nu}\)
\( \newcommand\Bxi{\mib\xi}\)
\( \newcommand\Bom{\mib\omicron}\)
\( \newcommand\Bpi{\mib\pi}\)
\( \newcommand\Bvarpi{\mib\varpi}\)
\( \newcommand\Brho{\mib\rho}\)
\( \newcommand\Bvrh{\mib\varrho}\)
\( \newcommand\Bsigma{\mib\sigma}\)
\( \newcommand\Bvsig{\mib\varsigma}\)
\( \newcommand\Btau{\mib\tau}\)
\( \newcommand\Bups{\mib\upsilon}\)
\( \newcommand\Bphi{\mib\phi}\)
\( \newcommand\Bvphi{\mib\vphi}\)
\( \newcommand\Bchi{\mib\chi}\)
\( \newcommand\Bpsi{\mib\psi}\)
\( \newcommand\Bomega{\mib\omega}\)
\( \newcommand\BGamma{\mib\Gamma}\)
\( \newcommand\BDelta{\mib\Delta}\)
\( \newcommand\BTheta{\mib\Theta}\)
\( \newcommand\BLambda{\mib\Lambda}\)
\( \newcommand\BXi{\mib\Xi}\)
\( \newcommand\BPi{\mib\Pi}\)
\( \newcommand\BSigma{\mib\Sigma}\)
\( \newcommand\BUps{\mib\Upsilon}\)
\( \newcommand\BPhi{\mib\Phi}\)
\( \newcommand\BPsi{\mib\Psi}\)
\( \newcommand\BOmega{\mib\Omega}\)
\( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\)
\( \newcommand\RGamma{ \Gamma}\)
\( \newcommand\RDelta{ \Delta}\)
\( \newcommand\RTheta{ \Theta}\)
\( \newcommand\RLambda{ \Lambda}\)
\( \newcommand\RXi{ \Xi}\)
\( \newcommand\RPi{ \Pi}\)
\( \newcommand\RSigma{ \Sigma}\)
\( \newcommand\RUps{ \Upsilon}\)
\( \newcommand\RPhi{ \Phi}\)
\( \newcommand\RPsi{ \Psi}\)
\( \newcommand\ROmega{ \Omega}\)
\( \newcommand\RA{ A}\)
\( \newcommand\RB{ B}\)
\( \newcommand\RC{ C}\)
\( \newcommand\RD{ D}\)
\( \newcommand\RE{ E}\)
\( \newcommand\RF{ F}\)
\( \newcommand\RG{ G}\)
\( \newcommand\RH{ H}\)
\( \newcommand\RI{ I}\)
\( \newcommand\RJ{ J}\)
\( \newcommand\RK{ K}\)
\( \newcommand\RL{ L}\)
\( \newcommand { M}\)
\( \newcommand\RN{ N}\)
\( \newcommand\RO{ O}\)
\( \newcommand\RP{ P}\)
\( \newcommand\RQ{ Q}\)
\( \newcommand\RR{ R}\)
\( \newcommand\RS{ S}\)
\( \newcommand\RT{ T}\)
\( \newcommand\RU{ U}\)
\( \newcommand\RV{ V}\)
\( \newcommand\RW{ W}\)
\( \newcommand\RX{ X}\)
\( \newcommand\RY{ Y}\)
\( \newcommand\RZ{ Z}\)
\( \newcommand\Ra{ a}\)
\( \newcommand\Rb{ b}\)
\( \newcommand\Rc{ c}\)
\( \newcommand\Rd{ d}\)
\( \newcommand\Re{ e}\)
\( \newcommand\Rf{ f}\)
\( \newcommand\Rg{ g}\)
\( \newcommand\Rh{ h}\)
\( \newcommand\Ri{ i}\)
\( \newcommand\Rj{ j}\)
\( \newcommand\Rk{ k}\)
\( \newcommand\Rl{ l}\)
\( \newcommand { m}\)
\( \newcommand\Rn{ n}\)
\( \newcommand\Ro{ o}\)
\( \newcommand\Rp{ p}\)
\( \newcommand\Rq{ q}\)
\( \newcommand\Rr{ r}\)
\( \newcommand\Rs{ s}\)
\( \newcommand\Rt{ t}\)
\( \newcommand\Ru{ u}\)
\( \newcommand\Rv{ v}\)
\( \newcommand\Rw{ w}\)
\( \newcommand\Rx{ x}\)
\( \newcommand\Ry{ y}\)
\( \newcommand\Rz{ z}\)
\( \newcommand\BBA{\boldsymbol\RA}\)
\( \newcommand\BBB{\boldsymbol\RB}\)
\( \newcommand\BBC{\boldsymbol\RC}\)
\( \newcommand\BBD{\boldsymbol\RD}\)
\( \newcommand\BBE{\boldsymbol\RE}\)
\( \newcommand\BBF{\boldsymbol\RF}\)
\( \newcommand\BBG{\boldsymbol\RG}\)
\( \newcommand\BBH{\boldsymbol\RH}\)
\( \newcommand\BBI{\boldsymbol\RI}\)
\( \newcommand\BBJ{\boldsymbol\RJ}\)
\( \newcommand\BBK{\boldsymbol\RK}\)
\( \newcommand\BBL{\boldsymbol\RL}\)
\( \newcommand\BBM{\boldsymbol }\)
\( \newcommand\BBN{\boldsymbol\RN}\)
\( \newcommand\BBO{\boldsymbol\RO}\)
\( \newcommand\BBP{\boldsymbol\RP}\)
\( \newcommand\BBQ{\boldsymbol\RQ}\)
\( \newcommand\BBR{\boldsymbol\RR}\)
\( \newcommand\BBS{\boldsymbol\RS}\)
\( \newcommand\BBT{\boldsymbol\RT}\)
\( \newcommand\BBU{\boldsymbol\RU}\)
\( \newcommand\BBV{\boldsymbol\RV}\)
\( \newcommand\BBW{\boldsymbol\RW}\)
\( \newcommand\BBX{\boldsymbol\RX}\)
\( \newcommand\BBY{\boldsymbol\RY}\)
\( \newcommand\BBZ{\boldsymbol\RZ}\)
\( \newcommand\BBa{\boldsymbol\Ra}\)
\( \newcommand\BBb{\boldsymbol\Rb}\)
\( \newcommand\BBc{\boldsymbol\Rc}\)
\( \newcommand\BBd{\boldsymbol\Rd}\)
\( \newcommand\BBe{\boldsymbol\Re}\)
\( \newcommand\BBf{\boldsymbol\Rf}\)
\( \newcommand\BBg{\boldsymbol\Rg}\)
\( \newcommand\BBh{\boldsymbol\Rh}\}\)
\( \newcommand\BBi{\boldsymbol\Ri}\)
\( \newcommand\BBj{\boldsymbol\Rj}\)
\( \newcommand\BBk{\boldsymbol\Rk}\)
\( \newcommand\BBl{boldsymbol\Rl}\)
\( \newcommand\BBm{\boldsymbol }\)
\( \newcommand\BBn{\boldsymbol\Rn}\)
\( \newcommand\BBo{\boldsymbol\Ro}\)
\( \newcommand\BBp{\boldsymbol\Rp}\)
\( \newcommand\BBq{\boldsymbol\Rq}\)
\( \newcommand\BBr{\boldsymbol\Rr}\)
\( \newcommand\BBs{\boldsymbol\Rs}\)
\( \newcommand\BBt{\boldsymbol\Rt}\)
\( \newcommand\BBu{\boldsymbol\Ru}\)
\( \newcommand\BBv{\boldsymbol\Rv}\)
\( \newcommand\BBw{\boldsymbol\Rw}\)
\( \newcommand\BBx{\boldsymbol\Rx}\)
\( \newcommand\BBy{\boldsymbol\Ry}\)
\( \newcommand\BBz{\boldsymbol\Rz}\)
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
\( \newcommand\bnabla{\boldsymbol{\nabla}}\)
\( \newcommand\Bell{\boldsymbol\ell}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \newcommand\ns{^\vphantom{*}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\)
\( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\)
\( \newcommand\etc{\it etc.\/}\)
\( \newcommand\etal{\it et al.\/}\)
\( \newcommand\opcit{\it op. cit.\/}\)
\( \newcommand\ie{\it i.e.\/}\)
\( \newcommand\Ie{\it I.e.\/}\)
\( \newcommand\viz{\it viz.\/}\)
\( \newcommand\eg{\it e.g.\/}\)
\( \newcommand\Eg{\it E.g.\/}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \def\sss#1{\scriptscriptstyle #1}\)
\( \def\ss#1{\scriptstyle #1}\)
\( \def\ssr#1{\scriptstyle #1}\)
\( \def\ssf#1{\scriptstyle #1}\)
\( \newcommand\NA{N_{\ssr{\!A}}}\)
\( \newcommand\lala{\langle\!\langle}\)
\( \newcommand\rara{\rangle\!\rangle}\)
\( \newcommand\blan{\big\langle}\)
\( \newcommand\bran{\big\rangle}\)
\( \newcommand\Blan{\Big\langle}\)
\( \newcommand\Bran{\Big\rangle}\)
\( \newcommand\intl{\int\limits}\)
\( \newcommand\half{\frac{1}{2}}\)
\( \newcommand\third{\frac{1}{3}}\)
\( \newcommand\fourth{\frac{1}{4}}\)
\( \newcommand\eighth{\frac{1}{8}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\)
\( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\)
\( \newcommand\det{\mathop{\textsf{det}}\,}\)
\( \def\tket#1{|  #1 \rangle}\)
\( \def\tbra#1{\langle #1|}\)
\( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\)
\( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\)
\( \def\sket#1{|  \, #1 \,  \rangle}\)
\( \def\sbra#1{\langle \,  #1 \, |}\)
\( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\)
\( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\)
\(\def\ket#1{\big| \, #1\, \big\rangle}\)
\( \def\bra#1{\big\langle \, #1 \, \big|}\)
\( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\)
\( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\)
\( \newcommand\pz{\partial}\)
\( \newcommand\pzb{\bar{\partial}}\)
\( \newcommand\svph{\vphantom{\int}}\)
\( \newcommand\vph{\vphantom{\sum_i}}\)
\( \newcommand\bvph{\vphantom{\sum_N^N}}\)
\( \newcommand\nd{^{\vphantom{\dagger}}}\)
\( \newcommand\ns{^{\vphantom{*}}}\)
\( \newcommand\yd{^\dagger}\)
\( \newcommand\zb{\bar z}\)
\( \newcommand\zdot{\dot z}\)
\( \newcommand\zbdot{\dot{\bar z}}\)
\( \newcommand\kB{k_{\sss{B}}}\)
\( \newcommand\kT{k_{\sss{B}}T}\)
\( \newcommand\gtau{g_\tau}\)
\( \newcommand\Htil{\tilde H}\)
\( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\)
\( \newcommand\pairm{(\phi\nd_0,J)}\)
\( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\)
\( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\)
\( \newcommand\pair{(\phi,J)}\)
\( \newcommand\Hz{H\nd_0}\)
\( \newcommand\Ho{H\nd_1}\)
\( \newcommand\Htz{\Htil\nd_0}\)
\( \newcommand\Hto{\Htil\nd_1}\)
\( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\)
\( \newcommand\csch{\,{ csch\,}}\)
\( \newcommand\ctnh{\,{ ctnh\,}}\)
\( \newcommand\ctn{\,{ ctn\,}}\)
\( \newcommand\sgn{\,{ sgn\,}}\)
\( \def\tmapright#1{\xrightarrow \limits^{#1}}\)
\( \def\bmapright#1{\xrightarrow\limits_{#1}}\)
\( \newcommand\hfb{\hfill\break}\)
\( \newcommand\Rep{\textsf{Re}\,}\)
\( \newcommand\Imp{\textsf{Im}\,}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\)
\( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\)
\( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

\( \def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}\)
\( \def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}\)
\( \def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}\)
\( \def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}\)
\( \newcommand\subA{\ns_\ssr{A}}\)
\( \newcommand\subB{\ns_\ssr{B}}\)
\( \newcommand\subC{\ns_\ssr{C}}\)
\( \newcommand\subD{\ns_\ssr{D}}\)
\( \newcommand\subAB{\ns_\ssr{AB}}\)
\( \newcommand\subBC{\ns_\ssr{BC}}\)
\( \newcommand\subCD{\ns_\ssr{CD}}\)
\( \newcommand\subDA{\ns_\ssr{DA}}\)
\( \def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }\)
\( \def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}\)
\( \newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}\)
\( \newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}\)
\( \newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}\)
\( \newcommand\cds{\,\bullet\,}\)
\( \newcommand\ccs{\,\circ\,}\)
\( \newcommand\nsub{_{\vphantom{\dagger}}}\)
\( \newcommand\rhohat{\hat\rho}\)
\( \newcommand\vrhhat{\hat\vrh}\)
\( \newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}\)
\( \newcommand\brangle{\big\rangle}\)
\( \newcommand\blangle{\big\langle}\)
\( \newcommand\vet{\tilde\ve}\)
\( \newcommand\zbar{\bar z}\)
\( \newcommand\ftil{\tilde f}\)
\( \newcommand\XBE{\RXi\ns_\ssr{BE}}\)
\( \newcommand\XFD{\RXi\ns_\ssr{FD}}\)
\( \newcommand\OBE{\Omega\ns_\ssr{BE}}\)
\( \newcommand\OFD{\Omega\ns_\ssr{FD}}\)
\( \newcommand\veF{\ve\ns_\RF}\)
\( \newcommand\kF{k\ns_\RF}\)
\( \newcommand\kFu{k\ns_{\RF\uar}}\)
\( \newcommand\SZ{\textsf Z}}\) \( \newcommand\kFd{k\ns_{\RF\dar}\)
\( \newcommand\muB{\mu\ns_\ssr{B}}\)
\( \newcommand\mutB{\tilde\mu}\ns_\ssr{B}\)
\( \newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}\)
\( \newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}\)
\( \newcommand\xhiOZ{\xhi^\ssr{OZ}}\)
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\jhz{\HJ(0)}\)
\( \newcommand\nda{\nd_\alpha}\)
\( \newcommand\ndap{\nd_{\alpha'}}\)
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/06:_Classical_Interacting_Systems/6.02:_Nonideal_Classical_Gases), /content/body/p[1]/span, line 1, column 23

\)
\( \newcommand\msa{m\ns_\ssr{A}}\)
\( \newcommand\msb{m\ns_\ssr{B}}\)
\( \newcommand\mss{m\ns_\Rs}\)
\( \newcommand\HBx{\hat\Bx}\)
\( \newcommand\HBy{\hat\By}\)
\( \newcommand\HBz{\hat\Bz}\)
\( \newcommand\thm{\theta\ns_m}\)
\( \newcommand\thp{\theta\ns_\phi}\)
\( \newcommand\mtil{\widetilde m}\)
\( \newcommand\phitil{\widetilde\phi}\)
\( \newcommand\delf{\delta\! f}\)
\( \newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}\)
\( \newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}\)
\( \newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}\)
\( \newcommand\vbar{\bar v}\)
\( \newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}\)
\( \newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}\)
\( \newcommand\gla{g\nd_{\RLambda\nd}}\)
\( \newcommand\TA{T\ns_\ssr{A}}\)
\( \newcommand\TB{T\ns_\ssr{B}}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \newcommand\NS{N\ns_{\textsf S}}\)

Let’s switch gears now and return to the study of continuous classical systems described by a Hamiltonian \(\HH\big(\{\Bx\ns_i\},\{\Bp\ns_i\}\big)\). In the next chapter, we will see how the critical properties of classical fluids can in fact be modeled by an appropriate lattice gas Ising model, and we’ll derive methods for describing the liquid-gas phase transition in such a model.

The Configuration Integral

Consider the ordinary canonical partition function for a nonideal system of identical point particles interacting via a central two-body potential \(u(r)\). We work in the ordinary canonical ensemble. The \(N\)-particle partition function is

\[\begin{split} Z(T,V,N)&={1\over N!}\!\int\!\prod_{i=1}^N {d^d\!p\ns_i\,d^d\!x\ns_i\over h^d}\> e^{-\HH/\kT}\\ &={\lambda_T^{-Nd}\over N!}\!\int\!\prod_{i=1}^Nd^d\!x\ns_i\>\exp\bigg(\!-{1\over\kT}\,\sum_{i<j}u\big(|\Bx\ns_i-\Bx\ns_j|\big)\bigg)\ . \end{split}\]

Here, we have assumed a many body Hamiltonian of the form

\[\HH=\sum_{i=1}^N {\Bp_i^2\over 2m} + \sum_{i<j}u\big(|\Bx\ns_i-\Bx\ns_j|\big)\ ,\]

in which massive nonrelativistic particles interact via a two-body central potential. As before, \(\lambda\ns_T=\sqrt{2\pi\hbar^2/m\kT\,}\) is the thermal wavelength. We can now write

\[Z(T,V,N)=\lambda_T^{-Nd}\,Q\ns_N(T,V)\ ,\]

where the configuration integral \(Q\ns_N(T,V)\) is given by

\[Q\ns_N(T,V)={1\over N!}\int\!\!d^d\!x\nd_1\cdots\int\!\! d^d\!x\nd_N\,\prod_{i<j} e^{-\beta u(r\ns_{ij})}\ . \label{zconf}\]

There are no general methods for evaluating the configurational integral exactly.

One-dimensional Tonks gas

The Tonks gas is a one-dimensional generalization of the hard sphere gas. Consider a one-dimensional gas of indistinguishable particles of mass \(m\) interacting via the potential

\[u(x-x')=\begin{cases}\infty & \hbox{ if}\ |x-x'| < a \\ 0 & \hbox{ if}\ |x-x'| \ge a\ . \end{cases}\]

Thus, the Tonks gas may be considered to be a gas of hard rods. The above potential guarantees that the portion of configuration space in which any rods overlap is forbidden in this model⁴. Let the gas be placed in a finite volume \(L\). The hard sphere nature of the particles means that no particle can get within a distance \(\half a\) of the ends at \(x=0\) and \(x=L\). That is, there is a one-body potential \(v(x)\) acting as well, where

\[v(x)=\begin{cases}\infty & \hbox{ if}\ x<\half a \\ 0 & \hbox{ if}\ \half a \le x \le L-\half a\\ \infty & \hbox{ if}\ x > L-\half a\ . \end{cases}\]

The configuration integral of the 1D Tonks gas is given by

\[Q\ns_N(T,L)={1\over N!}\int\limits_0^L\!dx\ns_1\cdots\int\limits_0^L\!dx\ns_N\> \xhi(x\ns_1,\ldots,x\ns_N)\ ,\]

where \(\xhi = e^{-U/k\ns_\RB T}\) is zero if any two ‘rods’ (of length \(a\)) overlap, or if any rod overlaps with either boundary at \(x=0\) and \(x=L\), and \(\xhi=1\) otherwise. Note that \(\xhi\) does not depend on temperature. Without loss of generality, we can integrate over the subspace where \(x\ns_1 < x\ns_2 < \cdots < x\ns_N\) and then multiply the result by \(N!\) . Clearly \(x\ns_j\) must lie to the right of \(x\ns_{j-1}+a\) and to the left of \(Y\ns_j\equiv L - (N-j) a - \half a\). Thus, the configurational integral is

\[\begin{split} Q\ns_N(T,L)&=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-1}+a}^{Y\ns_N} \!\!\!\!\!\!\! dx\ns_N\\ &=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-2}+a}^{Y\ns_{N-1}} \!\!\!\!\!\!\! dx\ns_{N-1}\,\big( Y\ns_{N-1}-x\ns_{N-1}\big)\\ &=\!\!\int\limits_{a/2}^{Y\ns_1}\!\!dx\ns_1 \!\! \int\limits_{x\ns_1+a}^{Y\ns_2}\!\!\!\!dx\ns_2\> \cdots \!\!\!\!\!\!\! \int\limits_{x\ns_{N-3}+a}^{Y\ns_{N-2}} \!\!\!\!\!\!\! dx\ns_{N-2}\>\half\big( Y\ns_{N-2}-x\ns_{N-2}\big)^2=\cdots \\ &= {1\over N!}\>\big(X\ns_1-\half a\big)^N = {1\over N!}\>(L-Na)^N\ . \end{split}\]

The partition function is \(Z(T,L,N)= \lambda_T^{-N}\,Q\ns_N(T,L)\) , and so the free energy is

\[F=-\kT\ln Z = -N\kT\Bigg\{-\ln\lambda\ns_T + 1 + \ln \bigg({L\over N}-a\bigg)\Bigg\}\ ,\]

where we have used Stirling’s rule to write \(\ln N!\approx N\ln N - N\). The pressure is

\[p=-{\pz F\over \pz L} = {\kT\over {L\over N} - a} = {n\kT\over 1-na}\ ,\]

where \(n=N/L\) is the one-dimensional density. Note that the pressure diverges as \(n\) approaches \(1/a\). The usual one-dimensional ideal gas law, \(pL=N\kT\), is replaced by \(pL\ns_{ eff}=N\kT\), where \(L\ns_{ eff}=L-Na\) is the ‘free’ volume obtained by subtracting the total "excluded volume" \(Na\) from the original volume \(L\). Note the similarity here to the van der Waals equation of state, \((p+av^{-2})(v-b)=RT\), where \(v=\NA V / N\) is the molar volume. Defining \({\tilde a}\equiv a/N_{\!\ssr{A}}^2\) and \({\tilde b}\equiv b/\NA\), we have

\[p+{\tilde a} n^2 = {n\kT\over 1-{\tilde b} n}\quad,\]

where \(n=\NA/v\) is the number density. The term involving the constant \({\tilde a}\) is due to the long-ranged attraction of atoms due to their mutual polarizability. The term involving \({\tilde b}\) is an excluded volume effect. The Tonks gas models only the latter.

Mayer Cluster Expansion

Let us return to the general problem of computing the configuration integral. Consider the function \(e^{-\beta u\ns_{ij}}\), where \(u\ns_{ij}\equiv u(|\Bx\ns_i-\Bx\ns_j|)\). We assume that at very short distances there is a strong repulsion between particles, \(u\ns_{ij}\to\infty\) as \(r\ns_{ij}=|\Bx\ns_i-\Bx\ns_j|\to 0\), and that \(u\ns_{ij}\to 0\) as \(r\ns_{ij}\to\infty\). Thus, \(e^{-\beta u\ns_{ij}}\) vanishes as \(r\ns_{ij}\to 0\) and approaches unity as \(r\ns_{ij}\to\infty\). For our purposes, it will prove useful to define the function

\[f(r)=e^{-\beta u(r)}-1\ ,\]

called the Mayer function after Josef Mayer. We may now write

\[Q\ns_N(T,V)={1\over N!}\int\!\!d^d\!x\nd_1\cdots\int\!\! d^d\!x\nd_N\,\prod_{i<j} \big(1+f\nd_{ij}\big)\ . \label{zmany}\]

Figure \(\PageIndex{1}\): Bottom panel: Lennard-Jones potential \(u(r)=4\eps \,\big(x^{-12}-x^{-6}\big)\), with \(x=r/\sigma\) and \(\eps=1\). Note the weak attractive tail and the strong repulsive core. Top panel: Mayer function \(f(r,T)=e^{-u(r)/k_{\ssr{B}}T}-1\) for \(k_{\ssr{B}}T=0.8\,\eps\) (blue), \(k_{\ssr{B}}T=1.5\,\eps\) (green), and \(k_{\ssr{B}}T=5\,\eps\) (red).

A typical potential we might consider is the semi-phenomenological Lennard-Jones potential,

\[u(r)=4\,\eps\,\bigg\{\Big({\sigma\over r}\Big)^{\!12}-\Big({\sigma\over r}\Big)^{\!6}\bigg\}\ .\]

This accounts for a long-distance attraction due to mutually induced electric dipole fluctuations, and a strong short-ranged repulsion, phenomenologically modelled with a \(r^{-12}\) potential, which mimics a hard core due to overlap of the atomic electron distributions. Setting \(u'(r)=0\) we obtain \(r^*=2^{1/6}\,\sigma\approx 1.12246\,\sigma\) at the minimum, where \(u(r^*)=-\eps\). In contrast to the Boltzmann weight \(e^{-\beta u(r)}\), the Mayer function \(f(r)\) vanishes as \(r\to\infty\), behaving as \(f(r)\sim -\beta u(r)\). The Mayer function also depends on temperature. Sketches of \(u(r)\) and \(f(r)\) for the Lennard-Jones model are shown in Figure \(\PageIndex{1}\).

The Lennard-Jones potential⁵ is realistic for certain simple fluids, but it leads to a configuration integral which is in general impossible to evaluate. Indeed, even a potential as simple as that of the hard sphere gas is intractable in more than one space dimension. We can however make progress by deriving a series expansion for the equation of state in powers of the particle density. This is known as the virial expansion. As was the case when we investigated noninteracting quantum statistics, it is convenient to work in the grand canonical ensemble and to derive series expansions for the density \(n(T,z)\) and the pressure \(p(T,z)\) in terms of the fugacity \(z\), then solve for \(z(T,n)\) to obtain \(p(T,n)\). These expansions in terms of fugacity have a nifty diagrammatic interpretation, due to Mayer.

We begin by expanding the product in Equation \ref{zmany} as

\[\prod_{i<j}\big(1+ f\ns_{ij}\big)=1+\sum_{i<j} f\ns_{ij} +\!\! \sum_{i<j\>,\>k<l\atop (ij)\ne(kl)} \!\! f\ns_{ij}\,f\ns_{kl} + \ldots\ .\]

As there are \(\half N(N-1)\) possible pairings, there are \(2^{N(N-1)/2}\) terms in the expansion of the above product. Each such term may be represented by a graph, as shown in Figure \(\PageIndex{2}\). For each such term, we draw a connection between dots representing different particles \(i\) and \(j\) if the factor \(f\nd_{ij}\) appears in the term under consideration. The contribution for any given graph may be written as a product over contributions from each of its disconnected component clusters. For example, in the case of the term in Figure \(\PageIndex{2}\), the contribution to the configurational integral would be

\[\begin{split} \RDelta Q &= {V^{N-11}\over N!}\int\!\!d^d\!x\nd_1\,d^d\!x\nd_4\,d^d\!x\nd_7\,d^d\!x\nd_9\ f\ns_{1,4}\,f\nd_{4,7}\,f\nd_{4,9}\,f\nd_{7,9}\\ &\hskip0.6in\times\int\!\!d^d\!x\nd_2\,d^d\!x\nd_5\,d^d\!x\nd_6\>f\nd_{2,5}\,f\nd_{2,6} \times\int\!\!d^d\!x\nd_3\,d^d\!x\nd_{10}\>f\nd_{3,10}\times\int\!\!d^d\!x\nd_8\,d^d\!x\nd_{11}\>f\nd_{8,11}\ . \end{split}\]

We will refer to a given product of Mayer functions which arises from this expansion as a term.

Figure \(\PageIndex{2}\): Diagrammatic interpretation of a term involving a product of eight Mayer functions.

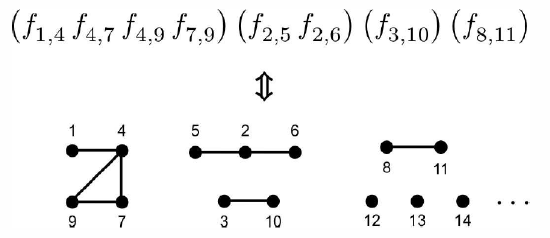
Figure 6.6: Left: John Lennard-Jones. Center: Catherine Zeta-Jones. Right: James Earl Jones.

The particular labels we assign to each vertex of a given graph don’t affect the overall value of the graph. Now a given unlabeled graph consists of a certain number of connected subgraphs. For a system with \(N\) particles, we may then write

\[N=\sum_\gamma m\nd_\gamma\,n\nd_\gamma\ ,\]

where \(\gamma\) ranges over all possible connected subgraphs, and

\[\begin{aligned} m\ns_\gamma&=\hbox{ number of connected subgraphs of type $\gamma$ in the unlabeled graph}\\ n\ns_\gamma&=\hbox{ number of vertices in the connected subgraph $\gamma$}\ .\end{aligned}\]

Note that the single vertex \(\bullet\) counts as a connected subgraph, with \(n\ns_\bullet=1\). We now ask: how many ways are there of assigning the \(N\) labels to the \(N\) vertices of a given unlabeled graph? One might first thing the answer is simply \(N!\), however this is too big, because different assignments of the labels to the vertices may not result in a distinct graph. To see this, consider the examples in Figure \(\PageIndex{3}\). In the first example, an unlabeled graph with four vertices consists of two identical connected subgraphs. Given any assignment of labels to the vertices, then, we can simply exchange the two subgraphs and get the same term. So we should divide \(N!\) by the product \(\prod_\gamma m\ns_\gamma !\) . But even this is not enough, because within each connected subgraph \(\gamma\) there may be permutations which leave the integrand unchanged, as shown in the second and third examples in Figure \(\PageIndex{3}\). We define the symmetry factor \(s\ns_\gamma\) as the number of permutations of the labels which leaves a given connected subgraphs \(\gamma\) invariant. Examples of symmetry factors are shown in Figure \(\PageIndex{4}\). Consider, for example, the third subgraph in the top row. Clearly one can rotate the figure about its horizontal symmetry axis to obtain a new labeling which represents the same term. This twofold axis is the only symmetry the diagram possesses, hence \(s\nd_\gamma=2\). For the first diagram in the second row, one can rotate either of the triangles about the horizontal symmetry axis. One can also rotate the figur e in the plane by \(180^\circ\) so as to exchange the two triangles. Thus, there are \(2\times 2\times 2=8\) symmetry operations which result in the same term, and \(s\nd_\gamma=8\). Finally, the last subgraph in the second row consists of five vertices each of which is connected to the other four. Therefore any permutation of the labels results in the same term, and \(s\nd_\gamma=5!=120\). In addition to dividing by the product \(\prod_\gamma m\nd_\gamma!\), we must then also divide by \(\prod_\gamma s_\gamma^{m\ns_\gamma}\).

Figure \(\PageIndex{3}\): Different assignations of labels to vertices may not result in a distinct term in the expansion of the configuration integral.

We can now write the partition function as

\[\begin{split} Z&={\lambda_T^{-Nd}\over N!}\sum_{ \{m\ns_\gamma\}} {N!\over\prod m_\gamma!\>s_\gamma^{m\ns_\gamma} }\cdot\prod_\gamma \Bigg(\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\Bigg)^{\!m\ns_\gamma}\!\cdot \delta\nd_{N\,,\,\sum m\ns_\gamma n\ns_\gamma}\\ &=\lambda_T^{-Nd}\sum_{ \{m\ns_\gamma\}}\prod_\gamma{\big(V b\ns_\gamma(T)\big)^{m\ns_\gamma}\over m\ns_\gamma!} \cdot\delta\nd_{N\,,\,\sum m\ns_\gamma n\ns_\gamma} \end{split}\]

where the product \(\prod_{i<j}^\gamma f\ns_{ij}\) is over all links in the subgraph \(\gamma\). The final Kronecker delta enforces the constraint \(N=\sum_\gamma m\ns_\gamma\,n\ns_\gamma\). We have defined the cluster integrals \(b\ns_\gamma\) as

\[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma} \prod_{i<j}^\gamma f\nd_{ij}\quad,\]

where we assume the limit \(V\to\infty\). Since \(f\nd_{ij}=f\big(|\Bx\nd_i-\Bx\nd_j|\big)\), the product \(\prod_{i<j}^\gamma f\nd_{ij}\) is invariant under simultaneous translation of all the coordinate vectors by any constant vector, and hence the integral over the \(n\ns_\gamma\) position variables contains exactly one factor of the volume, which cancels with the prefactor in the above definition of \(b\ns_\gamma\). Thus, each cluster integral is intensive⁶, scaling as \(V^0\).

If we compute the grand partition function, then the fixed \(N\) constraint is relaxed, and we can do the sums:

\[\begin{split} \Xi=e^{-\beta\Omega}&=\sum_{ \{m\ns_\gamma\} } \Big(e^{\beta\mu}\,\lambda_T^{-d}\Big)^{\sum m\ns_\gamma n\ns_\gamma} \prod_\gamma {1\over m\ns_\gamma !}\,\big(V \,b\ns_\gamma\big)^{m\ns_\gamma} \\ &=\prod_\gamma\sum_{m\ns_\gamma=0}^\infty {1\over m\ns_\gamma !}\>\Big(e^{\beta\mu}\, \lambda_T^{-d} \Big)^{m\ns_\gamma\,n\ns_\gamma}\big(V\,b\ns_\gamma\big)^{m\ns_\gamma}\\ &=\exp\bigg(V\sum_\gamma \big(e^{\beta\mu}\,\lambda_T^{-d}\big)^{n\ns_\gamma}\,b\ns_\gamma\bigg)\ . \end{split}\]

Thus,

\[\Omega(T,V,\mu)=-V\kT\,\sum_\gamma \big(e^{\beta\mu}\,\lambda_T^{-d}\big)^{n\ns_\gamma}\,b\ns_\gamma(T)\ ,\]

and we can write

\[\begin{split} p&=\kT\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\ , \label{pnofzT} \end{split}\]

where \(z=\exp(\beta\mu)\) is the fugacity, and where \(b\ns_\bullet\equiv 1\). As in the case of ideal quantum gas statistical mechanics, we can systematically invert the relation \(n=n(z,T)\) to obtain \(z=z(n,T)\), and then insert this into the equation for \(p(z,T)\) to obtain the equation of state \(p=p(n,T)\). This yields the virial expansion of the equation of state,

\[p=n\kT\Big\{1+B\ns_2(T)\,n + B\ns_3(T)\,n^2 + \ldots\Big\}\ .\]

Figure \(\PageIndex{4}\): The symmetry factor \(s_\gamma\) for a connected subgraph \(\gamma\) is the number of permutations of its indices which leaves the term \(\prod_{(ij)\in\gamma}f_{ij}\) invariant.

Lowest order expansion

We have

\[\begin{split} b\ns_-(T)&={1\over 2V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\>f\big(|\Bx\ns_1-\Bx\ns_2|\big)\\ &=\half\int\!\!d^d\!r\>f(r) \end{split}\]

and

\[\begin{split} b\ns_\wedge(T)&={1\over 2V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\>\!\int\!\!d^d\!x\ns_3\> f\big(|\Bx\ns_1-\Bx\ns_2|\big)\, f\big(|\Bx\ns_1-\Bx\ns_3|\big) \\ &=\half\int\!\!d^d\!r\!\int\!\!d^d\!r'\>f(r)\,f(r')=2\big(b\ns_-\big)^2 \end{split}\]

and

\[\begin{split} b\ns_\bigtriangleup(T)&={1\over 6V}\int\!\!d^d\!x\ns_1\!\int\!\!d^d\!x\ns_2\!\int\!\!d^d\!x\ns_3\> f\big(|\Bx\ns_1-\Bx\ns_2|\big) \> f\big(|\Bx\ns_1-\Bx\ns_3|\big)\> f\big(|\Bx\ns_2-\Bx\ns_3|\big)\\ &=\frac{1}{6}\int\!\!d^d\!r\!\int\!\!d^d\!r'\>f(r)\,f(r')\,f\big(|\Br-\Br'|\big)\ . \end{split}\]

We may now write

\[\begin{split} p&=\kT\Big\{ z\lambda_T^{-d} + \big(z\lambda_T^{-d} \big)^2\,b\ns_-(T) + \big(z\lambda_T^{-d} \big)^3\cdot\big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(z^4)\Big\}\\ n&=z\lambda_T^{-d} + 2\big(z\lambda_T^{-d} \big)^2\,b\ns_-(T) + 3\big(z\lambda_T^{-d} \big)^3\cdot\big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(z^4) \end{split}\]

We invert by writing

\[z\lambda_T^{-d} =n + \alpha\ns_2\,n^2 + \alpha\ns_3\,n^3 + \ldots \label{zln}\]

and substituting into the equation for \(n(z,T)\), yielding

\[n=(n + \alpha\ns_2\,n^2 + \alpha\ns_3\,n^3 ) + 2 (n+ \alpha\ns_2\,n^2 )^2\,b\ns_- + 3 n^3\, \big(b\ns_\wedge + b\nd_\bigtriangleup\big)+\CO(n^4)\ .\]

Thus,

\[0=(\alpha\ns_2+2 b\ns_-)\,n^2 + (\alpha\ns_3 + 4\alpha\ns_2\,b\ns_- + 3 b\ns_\wedge + 3 b\ns_\bigtriangleup)\,n^3 + \ldots\ .\]

We therefore conclude

\[\begin{split} \alpha\ns_2&=-2b\ns_- \\ \alpha\ns_3&=-4\alpha\ns_2\,b\ns_- - 3b\ns_\wedge - 3 b\ns_\bigtriangleup\\ &=8 b^2_- - 6 b^2_- - 3 b\ns_\bigtriangleup=2 b^2_- -3 b\ns_\bigtriangleup\ . \end{split}\]

We now insert Equation \ref{zln} with the determined values of \(\alpha\ns_{2,3}\) into the equation for \(p(z,T)\), obtaining

\[\begin{split} {p\over\kT}&=n-2b\ns_-n^2 + (2b^2_- -3b\ns_\bigtriangleup)\,n^3+(n-2b\ns_- n^2)^2 \,b\ns_-+n^3\,(2b^2_- + b\ns_\bigtriangleup) + \CO(n^4)\\ &=n-b\ns_-\,n^2 - 2b\ns_\bigtriangleup\,n^3 + \CO(n^4)\ . \end{split}\]

Thus,

\[B\ns_2(T)=-b\ns_-(T)\qquad,\qquad B\ns_3(T)=-2 b\ns_\bigtriangleup(T)\ .\]

Note that \(b\ns_\wedge\) does not contribute to \(B\ns_2\) – only \(\bigtriangleup\) appears. As we shall see, this is because the virial coefficients \(B\ns_j\) involve only cluster integrals \(b\ns_\gamma\) for one-particle irreducible clusters, those clusters which remain connected if any of the vertices plus all its links are removed.

One-particle irreducible clusters and the virial expansion

We start with Equation \ref{pnofzT} for \(p(T,z)\) and \(n(T,z)\),

\[\begin{split} p&=\kT\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma(T)\ , \end{split}\]

where \(b\ns_\gamma(T)\) for the connected cluster \(\gamma\) is given by

\[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\ .\]

It is convenient to work with dimensionless quantities, using \(\lambda_T^d\) as the unit of volume. To this end, define

\[\nu\equiv n\lambda_T^d\qquad,\qquad\pi\equiv p\lambda_T^d \qquad,\qquad c\ns_\gamma(T)\equiv b\ns_\gamma(T)\,\big(\lambda_T^d\big)^{\!n\ns_\gamma -1}\ ,\]

so that

\[\beta\pi=\sum_\gamma c\ns_\gamma\, z^{n\ns_\gamma}=\sum_{\ell=1}^\infty d\ns_\ell\,z^\ell\qquad,\qquad \nu=\sum_\gamma n\ns_\gamma c\ns_\gamma\, z^{n\ns_\gamma}=\sum_{l=1}^\infty \ell\, d\ns_\ell\,z^\ell\ ,\]

where

\[d\ns_\ell=\sum_\gamma c\ns_\gamma\,\delta\ns_{n\ns_\gamma\,,\,\ell}\]

is the sum over all connected clusters with \(\ell\) vertices. Here and henceforth, the functional dependence on \(T\) is implicit; \(\pi\) and \(\nu\) are regarded here as explicit functions of \(z\). We can, in principle, invert to obtain \(z(\nu)\). Let us write this inverse as

\[z(\nu)=\nu\,\exp\!\bigg(\!-\sum_{k=1}^\infty \beta\ns_k\,\nu^k\bigg)\ .\]

Ultimately we need to obtain expressions for the coefficients \(\beta\ns_k\), but let us first assume the above form and use it to write \(\pi\) in terms of \(\nu\). We have

\[\begin{split} \beta\pi&=\sum_{\ell=1}^\infty d\ns_\ell\,z^\ell = \int\limits_0^z\!\! d{\tilde z}\,\sum_{l=1}^\infty \ell\, d\ns_\ell\,{\tilde z}^{\ell-1} =\int\limits_0^\nu\!\! d{\tilde\nu}\,{d{\tilde z}\over d{\tilde\nu}} \, {\tilde\nu} \over {\tilde z} = \int\limits_0^\nu\!\! d{\tilde\nu}\,{d\ln {\tilde z}\over d\ln {\tilde\nu}}\\ &=\int\limits_0^\nu\!\!d{\tilde\nu}\,\bigg(1-\sum_{k=1}^\infty k\,\beta\ns_k\,{\tilde\nu}^k\bigg) =\nu -\sum_{k=1}^\infty {k\,\beta\ns_k\over k+1}\,\nu^{k+1}\equiv\sum_{k=1}^\infty \CB\ns_k\,\nu^k\ , \end{split}\]

where \(\CB\ns_k=B\ns_k\,\lambda_T^{-d(k-1)}\) is the dimensionless \(k^{ th}\) virial coefficient. Thus, \(\CB\ns_{k=1}=1\) and

\[\CB\ns_k=-{k-1\over k}\,\beta\ns_{k-1}\]

for \(k>1\). We may also obtain the cluster integrals \(d\ns_\ell\) in terms of the \(\beta\ns_k\) . To this end, note that \(\ell^2d_\ell\) is the coefficient of \(z^\ell\) in the function \(z\,d\nu/ dz\) , hence

\[\begin{split} \ell^2 d\ns_\ell&=\oint {dz\over 2\pi i z}\,{1\over z^\ell}\bigg(z\,{d\nu\over dz}\bigg) = \oint {d\nu\over 2\pi i}\,z^{-\ell} =\oint {d\nu\over 2\pi i}\,{1\over\nu^\ell}\,\prod_{k=1}^\infty e^{\ell\beta\ns_k\nu^k}\\ &=\oint {d\nu\over 2\pi i}\,{1\over\nu^\ell}\,\sum_{\{m\ns_k\}}\prod_{k=1}^\infty {(\ell\,\beta\ns_k)^{m\ns_k}\over m\ns_k!}\,\nu^{k m\ns_k} =\sum_{\{m\ns_k\}}\delta\ns_{\sum_k k m\ns_k\,,\,\ell-1}\prod_{k=1}^\infty {(\ell\,\beta\ns_k)^{m\ns_k}\over m\ns_k!}\ . \end{split}\]

Irreducible clusters

The clusters which contribute to \(d\ns_\ell\) are all connected, by definition. However, it is useful to make a further distinction based on the topology of connected clusters and define a connected cluster \(\gamma\) to be irreducible if, upon removing any site in \(\gamma\) and all the links connected to that site, the remaining sites of the cluster are still connected. The situation is depicted in Figure \(\PageIndex{5}\).

Figure \(\PageIndex{5}\): Connected versus irreducible clusters. Clusters (a) through (d) are irreducible in that they remain connected if any component site and its connecting links are removed. Cluster (e) is connected, but is reducible. Its integral \(c_\gamma\) may be reduced to a product over its irreducible components, each shown in a unique color.

For a reducible cluster \(\gamma\), the integral \(c\ns_\gamma\) is proportional to a product of cluster integrals over its irreducible components. Let us define the set \(\Gamma\ns_\ell\) as the set of all irreducible clusters of \(\ell\) vertices. It turns out that

\[\beta\ns_k(T)={1\over V\lambda_T^{(k-1)d}}{1\over k!}\!\sum_{\gamma\in \Gamma\ns_{k+1}}\!\! \int\!\!d^d\!x\ns_1\cdots\int\!\!d^d\!x\ns_k\prod_{\langle ij\rangle}^\gamma f\ns_{ij}\]

Thus, the virial coefficients \(B\ns_j(T)\) are obtained by summing a restricted set of cluster integrals, viz.

\[B\ns_j(T)=-{k-1\over k}\,\beta\ns_{k-1}(T)\,\lambda_T^{(k-1)d}\quad.\]

In the end, it turns out we don’t need the symmetry factors at all!

Cookbook Recipe

Just follow these simple steps!

• The pressure and number density are written as an expansion over unlabeled connected clusters \(\gamma\), viz. \[\begin{split} \beta p&=\sum_\gamma \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma\\ n&=\sum_\gamma n\ns_\gamma\, \big(z\lambda_T^{-d}\big)^{\!n\ns_\gamma}\,b\ns_\gamma\ . \end{split}\]
• For each term in each of these sums, draw the unlabeled connected cluster \(\gamma\).
• Assign labels \(1\,,\,2\,,\,\ldots\,,\,n\ns_\gamma\) to the vertices, where \(n\ns_\gamma\) is the total number of vertices in the cluster \(\gamma\). It doesn’t matter how you assign the labels.
• Write down the product \(\prod_{i<j}^\gamma f\ns_{ij}\). The factor \(f\ns_{ij}\) appears in the product if there is a link in your (now labeled) cluster between sites \(i\) and \(j\).
• The symmetry factor \(s\ns_\gamma\) is the number of elements of the symmetric group \(S\ns_{n\ns_\gamma}\) which leave the product \(\prod_{i<j}^\gamma f\ns_{ij}\) invariant. The identity permutation leaves the product invariant, so \(s\ns_\gamma\ge 1\).
• The cluster integral is \[b\ns_\gamma(T)\equiv {1\over s\ns_\gamma}\cdot{1\over V} \!\int\!\!d^d\!x\nd_1\cdots d^d\!x\nd_{n\ns_\gamma}\prod_{i<j}^\gamma f\nd_{ij}\ .\] Due to translation invariance, \(b\ns_\gamma(T)\propto V^0\). One can therefore set \(\Bx\ns_{n\ns_\gamma}\equiv 0\), eliminate the volume factor from the denominator, and perform the integral over the remaining \(n\ns_\gamma\!-\!1\) coordinates.
• This procedure generates expansions for \(p(T,z)\) and \(n(T,z)\) in powers of the fugacity \(z=e^{\beta\mu}\). To obtain something useful like \(p(T,n)\), we invert the equation \(n=n(T,z)\) to find \(z=z(T,n)\), and then substitute into the equation \(p=p(T,z)\) to obtain \(p=p\big(T,z(T,n)\big)=p(T,n)\). The result is the virial expansion, \[p=n\kT\,\Big\{1+B\ns_2(T)\,n + B\ns_3(T)\,n^2 + \ldots\Big\}\ ,\] where \[B\ns_k(T)=-{1\over k (k-2)!}\sum_{\gamma\in \Gamma\ns_k} \int\!\!d^d\!x\ns_1\cdots\!\!\int\!\!d^d\!x\ns_{k-1}\prod_{\langle ij\rangle}^\gamma f\ns_{ij}\] with \(\Gamma\ns_k\) the set of all one-particle irreducible \(j\)-site clusters.

Hard sphere gas in three dimensions

The hard sphere potential is given by

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ 0 & \hbox{ if $r>a$\ .} \end{cases} \label{hspot}\]

Here \(a\) is the diameter of the spheres. The corresponding Mayer function is then temperature independent, and given by

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ 0 & \hbox{ if $r>a$\ .} \end{cases}\]

We can change variables

\[b\ns_-(T)=\half\!\!\int\!\!d^3\!r\>f(r)=-\frac{2}{3}\pi a^3\ .\]

The calculation of \(b\ns_\bigtriangleup\) is more challenging. We have

\[b\ns_\bigtriangleup=\frac{1}{6}\!\!\int\!\!d^3\!\rho\!\int\!\!d^3\!r\>f(\rho)\,f(r)\, f\big(|\Br-\Brho|\big)\ .\]

We must first compute the volume of overlap for spheres of radius \(a\) (recall \(a\) is the diameter of the constituent hard sphere particles) centered at \(0\) and at \(\Brho\):

\[\begin{split} \CV&=\int\!\!d^3\!r\,f(r)\,f\big(|\Br-\Brho|\big)\\ \label{shaded} &=2\!\int\limits_{\rho/2}^a\!\!dz\>\pi(a^2-z^2)=\frac{4\pi }{3}a^3 - \pi a^2 \rho + \frac{\pi}{12}\,\rho^3\ . \end{split}\]

We then integrate over region \(|\Brho|<a\), to obtain

\[b\ns_\bigtriangleup=-\frac{1}{6}\cdot 4\pi\!\!\int\limits_0^a\!\!d\rho \> \rho^2\cdot \Big\{\frac{4\pi }{3}a^3 - \pi a^2 \rho + \frac{\pi}{12}\,\rho^3\Big\} =-\frac{5\pi^2}{36}\,a^6\ .\]

Thus,

\[p=n\kT\,\Big\{1+\frac{2\pi}{3}a^3 n + \frac{5\pi^2}{18} a^6 n^2 + \CO(n^3)\Big\}\ .\]

Figure \(\PageIndex{6}\): The overlap of hard sphere Mayer functions. The shaded volume is \(\CV\).

Weakly attractive tail

Suppose

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ -u\ns_0(r) & \hbox{ if $r>a$\ .} \end{cases}\]

Then the corresponding Mayer function is

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ e^{\beta u\ns_0(r)}-1 & \hbox{ if $r>a$\ .} \end{cases}\]

Thus,

\[b\ns_-(T)=\half\!\int\!\!d^3\!r\,f(r)=-\frac{2\pi}{3}a^3 + 2\pi\!\int\limits_a^\infty\!\!dr\,r^2\>\Big[e^{\beta u\ns_0(r)}-1\Big]\ .\]

Thus, the second virial coefficient is

\[B\ns_2(T)=-b\ns_-(T)\approx \frac{2\pi}{3}a^3 - {2\pi\over\kT}\!\int\limits_a^\infty\!\!dr\,r^2\,u\ns_0(r)\ ,\]

where we have assumed \(\kT\ll u\ns_0(r)\). We see that the second virial coefficient changes sign at some temperature \(T\ns_0\), from a negative low temperature value to a positive high temperature value.

Spherical Potential Well

Consider an attractive spherical well potential with an infinitely repulsive core,

\[u(r)=\begin{cases} \infty & \hbox{ if $r\le a$} \\ -\eps & \hbox{ if $a<r<R$}\\ 0 & \hbox{ if $r>R$}\ . \end{cases}\]

Then the corresponding Mayer function is

\[f(r)=\begin{cases}-1 & \hbox{ if $r\le a$} \\ e^{\beta \eps}-1 & \hbox{ if $a<r<R$}\\ 0 & \hbox{ if $r>R$}\ . \end{cases}\]

Writing \(s\equiv R/a\), we have

\[\begin{split} B\ns_2(T)&=-b\ns_-(T)=-\half\!\int\!\!d^3\!r\,f(r)\\ &=-{1\over 2}\,\bigg\{ (-1)\cdot\frac{4\pi}{3}a^3 + \big(e^{\beta\eps}-1\big)\cdot\frac{4\pi}{3}a^3 (s^3-1)\bigg\}\\ &=\frac{2\pi}{3}a^3\,\bigg\{1-(s^3-1)\big(e^{\beta\eps}-1\big)\bigg\}\ . \end{split}\]

To find the temperature \(T\ns_0\) where \(B\ns_2(T)\) changes sign, we set \(B\ns_2(T\ns_0)=0\) and obtain

\[\kB T\ns_0=\eps\bigg/\ln\!\bigg({s^3\over s^3-1}\bigg)\ .\]

Recall in our study of the thermodynamics of the Joule-Thompson effect in §1.10.6 that the throttling process is isenthalpic. The temperature change, when a gas is pushed (or escapes) through a porous plug from a high pressure region to a low pressure one is

\[\RDelta T=\int\limits_{p\ns_1}^{p\ns_2}\!\!dp\,\pabc{T}{p}{H}\ ,\]

where

\[\pabc{T}{p}{H}={1\over C\ns_p}\Bigg[ T\pabc{V}{T}{p}-V\Bigg]\ .\]

Appealing to the virial expansion, and working to lowest order in corrections to the ideal gas law, we have

\[p={N\over V}\,\kT + {N^2\over V^2}\,\kT\,B\ns_2(T)+\ldots\]

and we compute \(\big(\frac{\pz V}{\pz T}\big)\nd_p\) by seting

\[0=dp=-{N\kT\over V^2}\,dV + {N\kB\over V}\,dT - {2N^2\over V^3}\,\kT\,B\ns_2(T)\,dV +{N^2\over V^2}\,d\big(\kT\,B\ns_2(T)\big) + \ldots\ .\]

Figure \(\PageIndex{7}\): An attractive spherical well with a repulsive core \(u(r)\) and its associated Mayer function \(f(r)\).

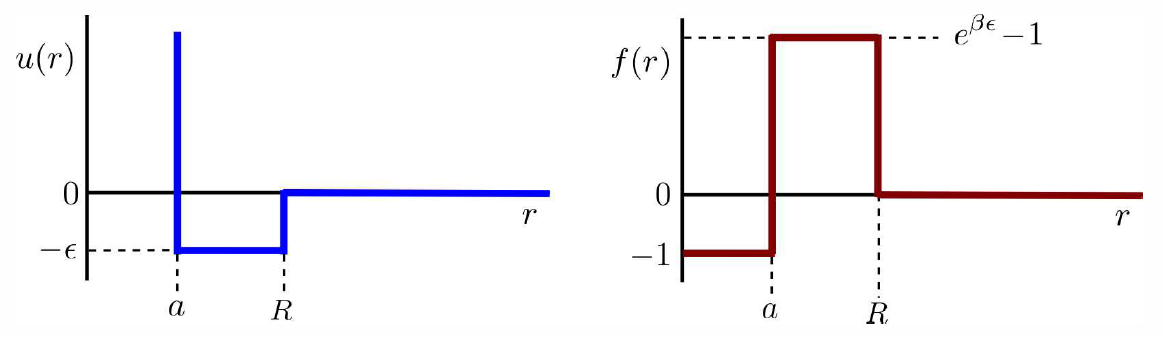
Dividing by \(dT\), we find

\[T\pabc{V}{T}{p}-V=N\Bigg[ T\,{\pz B\ns_2\over\pz T} - B\ns_2\Bigg]\ .\]

The temperature where \(\big(\frac{\pz T}{\pz p}\big)\nd_H\) changes sign is called the inversion temperature \(T^*\). To find the inversion point, we set \(T^*\, B'_2(T^*)=B\ns_2(T^*)\),

\[{d\ln B\ns_2\over d\ln T}\bigg|\nd_{T^*}\!\!=1\ .\]

If we approximate \(B\ns_2(T)\approx A-{B\over T}\), then the inversion temperature follows simply:

\[{B\over T^*}=A-{B\over T^*} \qquad\Longrightarrow\qquad T^*={2B\over A}\ .\]

Hard spheres with a hard wall

Consider a hard sphere gas in three dimensions in the presence of a hard wall at \(z=0\). The gas is confined to the region \(z>0\). The total potential energy is now

\[W(\xoN)=\sum_i v(\Bx\ns_i) + \sum_{i<j} u(\Bx\ns_i-\Bx\ns_j)\ ,\]

where

\[v(\Br)=v(z)=\begin{cases} \infty & { if}\quad z\le\half a \\ 0 & { if}\quad z > \half a\ , \end{cases}\]

and \(u(\Br)\) is given in Equation \ref{hspot}. The grand potential is written as a series in the total particle number \(N\), and is given by

\[\Xi=e^{-\beta\Omega} = 1+\xi\!\int\!\!d^3\!r\,e^{-\beta v(z)} + \half\xi^2\!\int\!\!d^3\!r\!\int\!\!d^3\!r'\>e^{-\beta v(z)}\,e^{-\beta v(z')}\, e^{-\beta u(\Br-\Br')} + \ldots\ ,\]

where \(\xi=z\,\lambda_T^{-3}\), with \(z=e^{\mu/\kT}\) the fugacity. Taking the logarithm, and invoking the Taylor series \(\ln(1+\delta)=\delta-\half\delta^2 + \third\delta^3 - \ldots\), we obtain

\[-\beta\Omega=\xi\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r + \half \xi^2\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r \!\!\!\int\limits_{z'>{a\over 2}}\!\!\!\!d^3\!r'\,\Big[ e^{-\beta u(\Br-\Br')}-1\Big]+ \ldots\]

The volume is \(V\!=\!\!\!\int\limits_{z>0} \!\!\!d^3\!r\). Dividing by \(V\), we have, in the thermodynamic limit,

\[\begin{split} -{\beta\Omega\over V}=\beta p&=\xi + \half \xi^2{1\over V}\!\!\!\int\limits_{z>{a\over 2}}\!\!\!\!d^3\!r \!\!\!\int\limits_{z'>{a\over 2}}\!\!\!\!d^3\!r'\,\Big[ e^{-\beta u(\Br-\Br')}-1\Big]+ \ldots\\ &=\xi-\frac{2}{3}\pi a^3\,\xi^2 + \CO(\xi^3)\ . \end{split}\]

The number density is

\[n=\xi\,{\pz\over\pz\xi}\,(\beta p)=\xi-\frac{4}{3}\pi a^3\,\xi^2 + \CO(\xi^3)\ ,\]

and inverting to obtain \(\xi(n)\) and then substituting into the pressure equation, we obtain the lowest order virial expansion for the equation of state,

\[p=\kT\,\Big\{n + \frac{2}{3}\pi a^3\,n^2 + \ldots\Big\}\ .\]

As expected, the presence of the wall does not affect a bulk property such as the equation of state.

Figure \(\PageIndex{8}\): In the presence of a hard wall, the Mayer sphere is cut off on the side closest to the wall. The resulting density \(n(z)\) vanishes for \(z<\half a\) since the center of each sphere must be at least one radius \((\half a)\) away from the wall. Between \(z=\half a\) and \(z=\frac{3}{2} a\) there is a density enhancement. If the calculation were carried out to higher order, \(n(z)\) would exhibit damped spatial oscillations with wavelength \(\lambda\sim a\).

Next, let us compute the number density \(n(z)\), given by

\[n(z)=\blangle\,\sum_i\delta(\Br-\Br\ns_i)\>\brangle\ .\]

Due to translational invariance in the \((x,y)\) plane, we know that the density must be a function of \(z\) alone. The presence of the wall at \(z=0\) breaks translational symmetry in the \(z\) direction. The number density is

\[\begin{split} n(z)&={ Tr} \bigg[e^{\beta(\mu\HN-\HH)}\,\sum_{i=1}^N\delta(\Br-\Br\ns_i)\bigg]\bigg/{ Tr}\ e^{\beta(\mu\HN-\HH)}\\ &=\Xi^{-1}\>\Bigg\{\xi\,e^{-\beta v(z)} + \xi^2\,e^{-\beta v(z)}\!\int\!\!d^3\!r'\,e^{-\beta v(z')}\,e^{-\beta u(\Br-\Br')} \, +\ \ldots\Bigg\}\\ &=\xi\,e^{-\beta v(z)} + \xi^2\,e^{-\beta v(z)}\!\int\!\!d^3\!r'\,e^{-\beta v(z')}\,\Big[e^{-\beta u(\Br-\Br')}-1\Big] \, +\ \ldots\ . \end{split}\]

Note that the term in square brackets in the last line is the Mayer function \(f(\Br-\Br')=e^{-\beta u(\Br-\Br')}-1\). Consider the function

\[e^{-\beta v(z)}\,e^{-\beta v(z')}\,f(\Br-\Br')=\begin{cases} 0 & \hbox{ if $z<\half a$ or $z'<\half a$}\\ 0 & \hbox{ if $|\Br-\Br'|>a$}\\ -1 & \hbox{ if $z>\half a$ and $z'>\half a$ and $|\Br-\Br'|<a$}\ . \end{cases}\]

Now consider the integral of the above function with respect to \(\Br'\). Clearly the result depends on the value of \(z\). If \(z>\frac{3}{2}a\), then there is no excluded region in \(\Br'\) and the integral is \((-1)\) times the full Mayer sphere volume, \(-\frac{4}{3}\pi a^3\). If \(z<\half a\) the integral vanishes due to the \(e^{-\beta v(z)}\) factor. For \(z\) infinitesimally larger than \(\half a\), the integral is \((-1)\) times half the Mayer sphere volume, \(-\frac{2}{3}\pi a^3\). For \(z\in\big[\frac{a}{2}\,,\,\frac{3a}{2}\big]\) the integral interpolates between \(-\frac{2}{3}\pi a^3\) and \(-\frac{4}{3}\pi a^3\). Explicitly, one finds by elementary integration,

\[\int\!\!d^3\!r'\>e^{-\beta v(z)}\,e^{-\beta v(z')}\,f(\Br-\Br')=\begin{cases} 0 & \hbox{ if $z<\half a$}\\ \left[ -1-\frac{3}{2} \big({z\over a}-\half\big) + \half \big({z\over a}-\half\big)^3 \right]\cdot\frac{2}{3}\pi a^3& \hbox{ if $\half a < z < \frac{3}{2} a$}\\ -{4\over 3}\pi a^3 & \hbox{ if $z>\frac{3}{2}a$}\ . \end{cases}\]

After substituting \(\xi=n+\frac{4}{3}\pi a^3 n^2 + \CO(n^3)\) to relate \(\xi\) to the bulk density \(n=n\ns_\infty\), we obtain the desired result:

\[n(z)=\begin{cases} 0 & \hbox{ if $z<\half a$}\\ n+\left[ 1 -\frac{3}{2} \big({z\over a}-\half\big) + \half \big({z\over a}-\half\big)^3 \right]\cdot\frac{2}{3}\pi a^3\,n^2 & \hbox{ if $\half a < z < \frac{3}{2} a$}\\ n & \hbox{ if $z>\frac{3}{2}a$}\ . \end{cases}\]

A sketch is provided in the right hand panel of Figure \(\PageIndex{8}\). Note that the density \(n(z)\) vanishes identically for \(z<\half\) due to the exclusion of the hard spheres by the wall. For \(z\) between \(\half a\) and \(\frac{3}{2} a\), there is a density enhancement, the origin of which has a simple physical interpretation. Since the wall excludes particles from the region \(z<\half\), there is an empty slab of thickness \(\half z\) coating the interior of the wall. There are then no particles in this region to exclude neighbors to their right, hence the density builds up just on the other side of this slab. The effect vanishes to the order of the calculation past \(z=\frac{3}{2}a\), where \(n(z)=n\) returns to its bulk value. Had we calculated to higher order, we’d have found damped oscillations with spatial period \(\lambda\sim a\).