8.4: Relaxation Time Approximation

\( \newcommand\bes{\begin{equation}\begin{split}}\)
\( \newcommand\ltwid{\propto}\)
\( \newcommand\ees{\end{split}\end{equation}}\)
\( \newcommand\mib{\mathbf}\)
\( \newcommand\Sa{\textsf a}\)
\( \newcommand\Sb{\textsf b}\)
\( \newcommand\Sc{\textsf c}\)
\( \newcommand\Sd{\textsf d}\)
\( \newcommand\Se{\textsf e}\)
\( \newcommand\Sf{\textsf f}\)
\( \newcommand\Sg{\textsf g}\)
\( \newcommand\Sh{\textsf h}\)
\( \newcommand\Si{\textsf i}\)
\( \newcommand\Sj{\textsf j}\)
\( \newcommand\Sk{\textsf k}\)
\( \newcommand\Sl{\textsf l}\)
\( \newcommand\Sm{\textsf m}\)
\( \newcommand\Sn{\textsf n}\)
\( \newcommand\So{\textsf o}\)
\( \newcommand\Sp{\textsf p}\)
\( \newcommand\Sq{\textsf q}\)
\( \newcommand\Sr{\textsf r}\)
\( \newcommand\Ss{\textsf s}\)
\( \newcommand\St{\textsf t}\)
\( \newcommand\Su{\textsf u}\)
\( \newcommand\Sv{\textsf v}\)
\( \newcommand\Sw{\textsf w}\)
\( \newcommand\Sx{\textsf x}\)
\( \newcommand\Sy{\textsf y}\)
\( \newcommand\Sz{\textsf z}\)
\( \newcommand\SA{\textsf A}\)
\( \newcommand\SB{\textsf B}\)
\( \newcommand\SC{\textsf C}\)
\( \newcommand\SD{\textsf D}\)
\( \newcommand\SE{\textsf E}\)
\( \newcommand\SF{\textsf F}\)
\( \newcommand\SG{\textsf G}\)
\( \newcommand\SH{\textsf H}\)
\( \newcommand\SI{\textsf I}\)
\( \newcommand\SJ{\textsf J}\)
\( \newcommand\SK{\textsf K}\)
\( \newcommand\SL{\textsf L}\)
\( \newcommand\SM{\textsf M}\)
\( \newcommand\SN{\textsf N}\)
\( \newcommand\SO{\textsf O}\)
\( \newcommand\SP{\textsf P}\)
\( \newcommand\SQ{\textsf Q}\)
\( \newcommand\SR{\textsf R}\)
\( \newcommand\SS{\textsf S}\)
\( \newcommand\ST{\textsf T}\)
\( \newcommand\SU{\textsf U}\)
\( \newcommand\SV{\textsf V}\)
\( \newcommand\SW{\textsf W}\)
\( \newcommand\SX{\textsf X}\)
\( \newcommand\SY{\textsf Y}\)
\( \newcommand\SZ{\textsf Z}\)
\( \newcommand\Ha{\hat a}\)
\( \newcommand\Hb{\hat b}\)
\( \newcommand\Hc{\hat c}\)
\( \newcommand\Hd{\hat d}\)
\( \newcommand\He{\hat e}\)
\( \newcommand\Hf{\hat f}\)
\( \newcommand\Hg{\hat g}\)
\( \newcommand\Hh{\hat h}\)
\( \newcommand\Hi{\hat \imath}\)
\( \newcommand\Hj{\hat \jmath}\)
\( \newcommand\Hk{\hat k}\)
\( \newcommand\Hl{\hat l}\)
\( \newcommand\Hm{\hat m}\)
\( \newcommand\Hn{\hat n}\)
\( \newcommand\Ho{\hat o}\)
\( \newcommand\Hp{\hat p}\)
\( \newcommand\Hq{\hat q}\)
\( \newcommand\Hr{\hat r}\)
\( \newcommand\Hs{\hat s}\)
\( \newcommand\Ht{\hat t}\)
\( \newcommand\Hu{\hat u}\)
\( \newcommand\Hv{\hat v}\)
\( \newcommand\Hw{\hat w}\)
\( \newcommand\Hx{\hat x}\)
\( \newcommand\Hy{\hat y}\)
\( \newcommand\Hz{\hat z}\)
\( \newcommand\HA{\hat A}\)
\( \newcommand\HB{\hat B}\)
\( \newcommand\HC{\hat C}\)
\( \newcommand\HD{\hat D}\)
\( \newcommand\HE{\hat E}\)
\( \newcommand\HF{\hat F}\)
\( \newcommand\HG{\hat G}\)
\( \newcommand\HH{\hat H}\)
\( \newcommand\HI{\hat I}\)
\( \newcommand\HJ{\hat J}\)
\( \newcommand\HK{\hat K}\)
\( \newcommand\HL{\hat L}\)
\( \newcommand\HM{\hat M}\)
\( \newcommand\HN{\hat N}\)
\( \newcommand\HO{\hat O}\)
\( \newcommand\HP{\hat P}\)
\( \newcommand\HQ{\hat Q}\)
\( \newcommand\HR{\hat R}\)
\( \newcommand\HS{\hat S}\)
\( \newcommand\HT{\hat T}\)
\( \newcommand\HU{\hat U}\)
\( \newcommand\HV{\hat V}\)
\( \newcommand\HW{\hat W}\)
\( \newcommand\HX{\hat X}\)
\( \newcommand\HY{\hat Y}\)
\( \newcommand\HZ{\hat Z}\)
\( \newcommand\Halpha{\hat\alpha}\)
\( \newcommand\Hbeta{\hat\beta}\)
\( \newcommand\Hgamma{\hat\gamma}\)
\( \newcommand\Hdelta{\hat\delta}\)
\( \newcommand\Hepsilon{\hat\epsilon}\)
\( \newcommand\Hvarepsilon{\hat\varepsilon}\)
\( \newcommand\Hzeta{\hat\zeta}\)
\( \newcommand\Heta{\hat\eta}\)
\( \newcommand\Htheta{\hat\theta}\)
\( \newcommand\Hvartheta{\hat\vartheta}\)
\( \newcommand\Hiota{\hat\iota}\)
\( \newcommand\Hkappa{\hat\kappa}\)
\( \newcommand\Hlambda{\hat\lambda}\)
\( \newcommand\Hmu{\hat\mu}\)
\( \newcommand\Hnu{\hat\nu}\)
\( \newcommand\Hxi{\hat\xi}\)
\( \newcommand\Hom{\hat\omicron}\)
\( \newcommand\Hpi{\hat\pi}\)
\( \newcommand\Hvarpi{\hat\varpi}\)
\( \newcommand\Hrho{\hat\rho}\)
\( \newcommand\Hvarrho{\hat\varrho}\)
\( \newcommand\Hsigma{\hat\sigma}\)
\( \newcommand\Hvarsigma{\hat\varsigma}\)
\( \newcommand\Htau{\var\tau}\)
\( \newcommand\Hupsilon{\hat\upsilon}\)
\( \newcommand\Hphi{\hat\phi}\)
\( \newcommand\Hvarphi{\hat\varphi}\)
\( \newcommand\Hchi{\hat\chi}\)
\( \newcommand\Hxhi{\hat\xhi}\)
\( \newcommand\Hpsi{\hat\psi}\)
\( \newcommand\Homega{\hat\omega}\)
\( \newcommand\HGamma{\hat\Gamma}\)
\( \newcommand\HDelta{\hat\Delta}\)
\( \newcommand\HTheta{\hat\Theta}\)
\( \newcommand\HLambda{\hat\Lambda}\)
\( \newcommand\HXi{\hat\Xi}\)
\( \newcommand\HPi{\hat\Pi}\)
\( \newcommand\HSigma{\hat\Sigma}\)
\( \newcommand\HUps{\hat\Upsilon}\)
\( \newcommand\HPhi{\hat\Phi}\)
\( \newcommand\HPsi{\hat\Psi}\)
\( \newcommand\HOmega{\hat\Omega}\)
\( \newcommand\xhat{\hat\Bx}\)
\( \newcommand\yhat{\hat\By}\)
\( \newcommand\zhat{\hat\Bz}\)
\( \newcommand\ehat{\hat\Be}\)
\( \newcommand\khat{\hat\Bk}\)
\( \newcommand\nhat{\hat\Bn}\)
\( \newcommand\rhat{\hat\Br}\)
\( \newcommand\phihat{\hat\Bphi}\)
\( \newcommand\thetahat{\hat\Btheta}\)
\( \newcommand\MA{\mathbb A}\)
\( \newcommand\MB{\mathbb B}\)
\( \newcommand\MC{\mathbb C}\)
\( \newcommand\MD{\mathbb D}\)
\( \newcommand\ME{\mathbb E}\)
\( \newcommand\MF{\mathbb F}\)
\( \newcommand\MG{\mathbb G}\)
\( \newcommand\MH{\mathbb H}\)
\( \newcommand\MI{\mathbb I}\)
\( \newcommand\MJ{\mathbb J}\)
\( \newcommand\MK{\mathbb K}\)
\( \newcommand\ML{\mathbb L}\)
\( \newcommand\MM{\mathbb M}\)
\( \newcommand\MN{\mathbb N}\)
\( \newcommand\MO{\mathbb O}\)
\( \newcommand\MP{\mathbb P}\)
\( \newcommand\MQ{\mathbb Q}\)
\( \newcommand\MR{\mathbb R}\)
\( \newcommand\MS{\mathbb S}\)
\( \newcommand\MT{\mathbb T}\)
\( \newcommand\MU{\mathbb U}\)
\( \newcommand\MV{\mathbb V}\)
\( \newcommand\MW{\mathbb W}\)
\( \newcommand\MX{\mathbb X}\)
\( \newcommand\MY{\mathbb Y}\)
\( \newcommand\MZ{\mathbb Z}\)
\( \newcommand\CA{\mathcal A}\)
\( \newcommand\CB{\mathcal B}\)
\( \newcommand\CC{\mathcal C}\)
\( \newcommand\CD{\mathcal D}\)
\( \newcommand\CE{\mathcal E}\)
\( \newcommand\CF{\mathcal F}\)
\( \newcommand\CG{\mathcal G}\)
\( \newcommand\CH{\mathcal H}\)
\( \newcommand\CI{\mathcal I}\)
\( \newcommand\CJ{\mathcal J}\)
\( \newcommand\CK{\mathcal K}\)
\( \newcommand\CL{\mathcal L}\)
\( \newcommand\CM{\mathcal M}\)
\( \newcommand\CN{\mathcal N}\)
\( \newcommand\CO{\mathcal O}\)
\( \newcommand\CP{\mathcal P}\)
\( \newcommand\CQ{\mathcal Q}\)
\( \newcommand\CR{\mathcal R}\)
\( \newcommand\CS{\mathcal S}\)
\( \newcommand\CT{\mathcal T}\)
\( \newcommand\CU{\mathcal U}\)
\( \newcommand\CV{\mathcal V}\)
\( \newcommand\CW{\mathcal W}\)
\( \newcommand\CX{\mathcal X}\)
\( \newcommand\CY{\mathcal Y}\)
\( \newcommand\CZ{\mathcal Z}\)
\( \newcommand\Fa{\mathfrak a}\)
\( \newcommand\Fb{\mathfrak b}\)
\( \newcommand\Fc{\mathfrak c}\)
\( \newcommand\Fd{\mathfrak d}\)
\( \newcommand\Fe{\mathfrak e}\)
\( \newcommand\Ff{\mathfrak f}\)
\( \newcommand\Fg{\mathfrak g}\)
\( \newcommand\Fh{\mathfrak h}\)
\( \newcommand\Fi{\mathfrak i}\)
\( \newcommand\Fj{\mathfrak j}\)
\( \newcommand\Fk{\mathfrak k}\)
\( \newcommand\Fl{\mathfrak l}\)
\( \newcommand\Fm{\mathfrak m}\)
\( \newcommand\Fn{\mathfrak n}\)
\( \newcommand\Fo{\mathfrak o}\)
\( \newcommand\Fp{\mathfrak p}\)
\( \newcommand\Fq{\mathfrak q}\)
\( \newcommand\Fr{\mathfrak r}\)
\( \newcommand\Fs{\mathfrak s}\)
\( \newcommand\Ft{\mathfrak t}\)
\( \newcommand\Fu{\mathfrak u}\)
\( \newcommand\Fv{\mathfrak v}\)
\( \newcommand\Fw{\mathfrak w}\)
\( \newcommand\Fx{\mathfrak x}\)
\( \newcommand\Fy{\mathfrak y}\)
\( \newcommand\Fz{\mathfrak z}\)
\( \newcommand\FA{\mathfrak A}\)
\( \newcommand\FB{\mathfrak B}\)
\( \newcommand\FC{\mathfrak C}\)
\( \newcommand\FD{\mathfrak D}\)
\( \newcommand\FE{\mathfrak E}\)
\( \newcommand\FF{\mathfrak F}\)
\( \newcommand\FG{\mathfrak G}\)
\( \newcommand\FH{\mathfrak H}\)
\( \newcommand\FI{\mathfrak I}\)
\( \newcommand\FJ{\mathfrak J}\)
\( \newcommand\FK{\mathfrak K}\)
\( \newcommand\FL{\mathfrak L}\)
\( \newcommand\FM{\mathfrak M}\)
\( \newcommand\FN{\mathfrak N}\)
\( \newcommand\FO{\mathfrak O}\)
\( \newcommand\FP{\mathfrak P}\)
\( \newcommand\FQ{\mathfrak Q}\)
\( \newcommand\FR{\mathfrak R}\)
\( \newcommand\FS{\mathfrak S}\)
\( \newcommand\FT{\mathfrak T}\)
\( \newcommand\FU{\mathfrak U}\)
\( \newcommand\FV{\mathfrak V}\)
\( \newcommand\FW{\mathfrak W}\)
\( \newcommand\FX{\mathfrak X}\)
\( \newcommand\FY{\mathfrak Y}\)
\( \newcommand\FZ{\mathfrak Z}\)
\( \newcommand\Da{\dot a}\)
\( \newcommand\Db{\dot b}\)
\( \newcommand\Dc{\dot c}\)
\( \newcommand\Dd{\dot d}\)
\( \newcommand\De{\dot e}\)
\( \newcommand\Df{\dot f}\)
\( \newcommand\Dg{\dot g}\)
\( \newcommand\Dh{\dot h}\)
\( \newcommand\Di{\dot \imath}\)
\( \newcommand\Dj{\dot \jmath}\)
\( \newcommand\Dk{\dot k}\)
\( \newcommand\Dl{\dot l}\)
\( \newcommand\Dm{\dot m}\)
\( \newcommand\Dn{\dot n}\)
\( \newcommand\Do{\dot o}\)
\( \newcommand\Dp{\dot p}\)
\( \newcommand\Dq{\dot q}\)
\( \newcommand\Dr{\dot r}\)
\( \newcommand\Ds{\dot s}\)
\( \newcommand\Dt{\dot t}\)
\( \newcommand\Du{\dot u}\)
\( \newcommand\Dv{\dot v}\)
\( \newcommand\Dw{\dot w}\)
\( \newcommand\Dx{\dot x}\)
\( \newcommand\Dy{\dot y}\)
\( \newcommand\Dz{\dot z}\)
\( \newcommand\DA{\dot A}\)
\( \newcommand\DB{\dot B}\)
\( \newcommand\DC{\dot C}\)
\( \newcommand\DD{\dot D}\)
\( \newcommand\DE{\dot E}\)
\( \newcommand\DF{\dot F}\)
\( \newcommand\DG{\dot G}\)
\( \newcommand\DH{\dot H}\)
\( \newcommand\DI{\dot I}\)
\( \newcommand\DJ{\dot J}\)
\( \newcommand\DK{\dot K}\)
\( \newcommand\DL{\dot L}\)
\( \newcommand\DM{\dot M}\)
\( \newcommand\DN{\dot N}\)
\( \newcommand\DO{\dot O}\)
\( \newcommand\DP{\dot P}\)
\( \newcommand\DQ{\dot Q}\)
\( \newcommand\DR{\dot R}\)
\( \newcommand\DS{\dot S}\)
\( \newcommand\DT{\dot T}\)
\( \newcommand\DU{\dot U}\)
\( \newcommand\DV{\dot V}\)
\( \newcommand\DW{\dot W}\)
\( \newcommand\DX{\dot X}\)
\( \newcommand\DY{\dot Y}\)
\( \newcommand\DZ{\dot Z}\)
\( \newcommand\Dalpha

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dbeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dgamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[3], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Ddelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[4], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Depsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[5], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvarepsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[6], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dzeta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[7], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Deta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[8], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dtheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[9], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dvartheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[10], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Diota

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[11], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dkappa

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[12], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dlambda

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[13], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Dmu{\dot\mu}\)
\( \newcommand\Dnu{\dot\nu}\)
\( \newcommand\Dxi{\dot\xi}\)
\( \newcommand\Dom{\dot\omicron}\)
\( \newcommand\Dpi{\dot\pi}\)
\( \newcommand\Dvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[14], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Drho{\dot\rho}\)
\( \newcommand\Dvarrho{\dot\varrho}\)
\( \newcommand\Dsigma{\dot\sigma}\)
\( \newcommand\Dvarsigma{\dot\varsigma}\)
\( \newcommand\Dtau{\var\tau}\)
\( \newcommand\Dupsilon{\dot\upsilon}\)
\( \newcommand\Dphi{\dot\phi}\)
\( \newcommand\Dvarphi{\dot\varphi}\)
\( \newcommand\Dchi{\dot\chi}\)
\( \newcommand\Dpsi{\dot\psi}\)
\( \newcommand\Domega{\dot\omega}\)
\( \newcommand\DGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[15], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[16], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DTheta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[17], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\DLambda{\dot\Lambda}\)
\( \newcommand\DXi{\dot\Xi}\)
\( \newcommand\DPi{\dot\Pi}\)
\( \newcommand\DSigma{\dot\Sigma}\)
\( \newcommand\DUps{\dot\Upsilon}\)
\( \newcommand\DPhi{\dot\Phi}\)
\( \newcommand\DPsi{\dot\Psi}\)
\( \newcommand\DOmega{\dot\Omega}\)
\( \newcommand\Va{\vec a}\)
\( \newcommand\Vb{\vec b}\)
\( \newcommand\Vc{\vec c}\)
\( \newcommand\Vd{\vec d}\)
\( \newcommand\Ve{\vec e}\)
\( \newcommand\Vf{\vec f}\)
\( \newcommand\Vg{\vec g}\)
\( \newcommand\Vh{\vec h}\)
\( \newcommand\Vi{\vec \imath}\)
\( \newcommand\Vj{\vec \jmath}\)
\( \newcommand\Vk{\vec k}\)
\( \newcommand\Vl{\vec l}\)
\( \newcommand\Vm{\vec m}\)
\( \newcommand\Vn{\vec n}\)
\( \newcommand\Vo{\vec o}\)
\( \newcommand\Vp{\vec p}\)
\( \newcommand\Vq{\vec q}\)
\( \newcommand\Vr{\vec r}\)
\( \newcommand\Vs{\vec s}\)
\( \newcommand\Vt{\vec t}\)
\( \newcommand\Vu{\vec u}\)
\( \newcommand\Vv{\vec v}\)
\( \newcommand\Vw{\vec w}\)
\( \newcommand\Vx{\vec x}\)
\( \newcommand\Vy{\vec y}\)
\( \newcommand\Vz{\vec z}\)
\( \newcommand\VA{\vec A}\)
\( \newcommand\VB{\vec B}\)
\( \newcommand\VC{\vec C}\)
\( \newcommand\VD{\vec D}\)
\( \newcommand\VE{\vec E}\)
\( \newcommand\VF{\vec F}\)
\( \newcommand\VG{\vec G}\)
\( \newcommand\VH{\vec H}\)
\( \newcommand\VI{\vec I}\)
\( \newcommand\VJ{\vec J}\)
\( \newcommand\VK{\vec K}\)
\( \newcommand\VL{\vec L}\)
\( \newcommand\VM{\vec M}\)
\( \newcommand\VN{\vec N}\)
\( \newcommand\VO{\vec O}\)
\( \newcommand\VP{\vec P}\)
\( \newcommand\VQ{\vec Q}\)
\( \newcommand\VR{\vec R}\)
\( \newcommand\VS{\vec S}\)
\( \newcommand\VT{\vec T}\)
\( \newcommand\VU{\vec U}\)
\( \newcommand\VV{\vec V}\)
\( \newcommand\VW{\vec W}\)
\( \newcommand\VX{\vec X}\)
\( \newcommand\VY{\vec Y}\)
\( \newcommand\VZ{\vec Z}\)
\( \newcommand\Valpha{\vec\alpha}\)
\( \newcommand\Vbeta{\vec\beta}\)
\( \newcommand\Vgamma{\vec\gamma}\)
\( \newcommand\Vdelta{\vec\delta}\)
\( \newcommand\Vepsilon{\vec\epsilon}\)
\( \newcommand\Vvarepsilon{\vec\varepsilon}\)
\( \newcommand\Vzeta{\vec\zeta}\)
\( \newcommand\Veta{\vec\eta}\)
\( \newcommand\Vtheta{\vec\theta}\)
\( \newcommand\Vvartheta{\vec\vartheta}\)
\( \newcommand\Viota{\vec\iota}\)
\( \newcommand\Vkappa{\vec\kappa}\)
\( \newcommand\Vlambda{\vec\lambda}\)
\( \newcommand\Vmu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[18], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vnu

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[19], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vxi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[20], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vom

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[21], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[22], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarpi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[23], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[24], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarrho

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[25], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[26], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarsigma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[27], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vtau

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[28], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vupsilon

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[29], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[30], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vvarphi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[31], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vchi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[32], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vpsi

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[33], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\Vomega

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[34], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VGamma

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[35], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VDelta

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/p[1]/span[36], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\VTheta{\vec\Theta}\)
\( \newcommand\VLambda{\vec\Lambda}\)
\( \newcommand\VXi{\vec\Xi}\)
\( \newcommand\VPi{\vec\Pi}\)
\( \newcommand\VSigma{\vec\Sigma}\)
\( \newcommand\VUps{\vec\Upsilon}\)
\( \newcommand\VPhi{\vec\Phi}\)
\( \newcommand\VPsi{\vec\Psi}\)
\( \newcommand\VOmega{\vec\Omega}\)
\( \newcommand\BA{\mib A}\)
\( \newcommand\BB{\mib B}\)
\( \newcommand\BC{\mib C}\)
\( \newcommand\BD{\mib D}\)
\( \newcommand\BE{\mib E}\)
\( \newcommand\BF{\mib F}\)
\( \newcommand\BG{\mib G}\)
\( \newcommand\BH{\mib H}\)
\( \newcommand\BI{\mib I}}\)
\( \newcommand\BJ{\mib J}\)
\( \newcommand\BK{\mib K}\)
\( \newcommand\BL{\mib L}\)
\( \newcommand\BM{\mib M}\)
\( \newcommand\BN{\mib N}\)
\( \newcommand\BO{\mib O}\)
\( \newcommand\BP{\mib P}\)
\( \newcommand\BQ{\mib Q}\)
\( \newcommand\BR{\mib R}\)
\( \newcommand\BS{\mib S}\)
\( \newcommand\BT{\mib T}\)
\( \newcommand\BU{\mib U}\)
\( \newcommand\BV{\mib V}\)
\( \newcommand\BW{\mib W}\)
\( \newcommand\BX{\mib X}\)
\( \newcommand\BY{\mib Y}\)
\( \newcommand\BZ{\mib Z}\)
\( \newcommand\Ba{\mib a}\)
\( \newcommand\Bb{\mib b}\)
\( \newcommand\Bc{\mib c}\)
\( \newcommand\Bd{\mib d}\)
\( \newcommand\Be{\mib e}\)
\( \newcommand\Bf{\mib f}\)
\( \newcommand\Bg{\mib g}\)
\( \newcommand\Bh{\mib h}\)
\( \newcommand\Bi{\mib i}\)
\( \newcommand\Bj{\mib j}\)
\( \newcommand\Bk{\mib k}\)
\( \newcommand\Bl{\mib l}\)
\( \newcommand\Bm{\mib m}\)
\( \newcommand\Bn{\mib n}\)
\( \newcommand\Bo{\mib o}\)
\( \newcommand\Bp{\mib p}\)
\( \newcommand\Bq{\mib q}\)
\( \newcommand\Br{\mib r}\)
\( \newcommand\Bs{\mib s}\)
\( \newcommand\Bt{\mib t}\)
\( \newcommand\Bu{\mib u}\)
\( \newcommand\Bv{\mib v}\)
\( \newcommand\Bw{\mib w}\)
\( \newcommand\Bx{\mib x}\)
\( \newcommand\By{\mib y}\)
\( \newcommand\Bz{\mib z}\)\)
\( \newcommand\vrh{\varrho}\)
\( \newcommand\vsig{\varsigma}\)
\( \newcommand\ups{\upsilon}\)
\( \newcommand\eps{\epsilon}\)
\( \newcommand\ve{\varepsilon}\)
\( \newcommand\vth{\vartheta}\)
\( \newcommand\vphi{\varphi}\)
\( \newcommand\xhi{\chi}\)
\( \newcommand\Ups{\Upsilon}\)
\( \newcommand\Balpha{\mib\alpha}\)
\( \newcommand\Bbeta{\mib\beta}\)
\( \newcommand\Bgamma{\mib\gamma}\)
\( \newcommand\Bdelta{\mib\delta}\)
\( \newcommand\Beps{\mib\epsilon}\)
\( \newcommand\Bve{\mib\varepsilon}\)
\( \newcommand\Bzeta{\mib\zeta}\)
\( \newcommand\Beta{\mib\eta}\)
\( \newcommand\Btheta{\mib\theta}\)
\( \newcommand\Bvth{\mib\vartheta}\)
\( \newcommand\Biota{\mib\iota}\)
\( \newcommand\Bkappa{\mib\kappa}\)
\( \newcommand\Blambda{\mib\lambda}\)
\( \newcommand\Bmu{\mib\mu}\)
\( \newcommand\Bnu{\mib\nu}\)
\( \newcommand\Bxi{\mib\xi}\)
\( \newcommand\Bom{\mib\omicron}\)
\( \newcommand\Bpi{\mib\pi}\)
\( \newcommand\Bvarpi{\mib\varpi}\)
\( \newcommand\Brho{\mib\rho}\)
\( \newcommand\Bvrh{\mib\varrho}\)
\( \newcommand\Bsigma{\mib\sigma}\)
\( \newcommand\Bvsig{\mib\varsigma}\)
\( \newcommand\Btau{\mib\tau}\)
\( \newcommand\Bups{\mib\upsilon}\)
\( \newcommand\Bphi{\mib\phi}\)
\( \newcommand\Bvphi{\mib\vphi}\)
\( \newcommand\Bchi{\mib\chi}\)
\( \newcommand\Bpsi{\mib\psi}\)
\( \newcommand\Bomega{\mib\omega}\)
\( \newcommand\BGamma{\mib\Gamma}\)
\( \newcommand\BDelta{\mib\Delta}\)
\( \newcommand\BTheta{\mib\Theta}\)
\( \newcommand\BLambda{\mib\Lambda}\)
\( \newcommand\BXi{\mib\Xi}\)
\( \newcommand\BPi{\mib\Pi}\)
\( \newcommand\BSigma{\mib\Sigma}\)
\( \newcommand\BUps{\mib\Upsilon}\)
\( \newcommand\BPhi{\mib\Phi}\)
\( \newcommand\BPsi{\mib\Psi}\)
\( \newcommand\BOmega{\mib\Omega}\)
\( \newcommand\Bxhi{\raise.35ex\hbox{$\Bchi$}}\)
\( \newcommand\RGamma{ \Gamma}\)
\( \newcommand\RDelta{ \Delta}\)
\( \newcommand\RTheta{ \Theta}\)
\( \newcommand\RLambda{ \Lambda}\)
\( \newcommand\RXi{ \Xi}\)
\( \newcommand\RPi{ \Pi}\)
\( \newcommand\RSigma{ \Sigma}\)
\( \newcommand\RUps{ \Upsilon}\)
\( \newcommand\RPhi{ \Phi}\)
\( \newcommand\RPsi{ \Psi}\)
\( \newcommand\ROmega{ \Omega}\)
\( \newcommand\RA{ A}\)
\( \newcommand\RB{ B}\)
\( \newcommand\RC{ C}\)
\( \newcommand\RD{ D}\)
\( \newcommand\RE{ E}\)
\( \newcommand\RF{ F}\)
\( \newcommand\RG{ G}\)
\( \newcommand\RH{ H}\)
\( \newcommand\RI{ I}\)
\( \newcommand\RJ{ J}\)
\( \newcommand\RK{ K}\)
\( \newcommand\RL{ L}\)
\( \newcommand { M}\)
\( \newcommand\RN{ N}\)
\( \newcommand\RO{ O}\)
\( \newcommand\RP{ P}\)
\( \newcommand\RQ{ Q}\)
\( \newcommand\RR{ R}\)
\( \newcommand\RS{ S}\)
\( \newcommand\RT{ T}\)
\( \newcommand\RU{ U}\)
\( \newcommand\RV{ V}\)
\( \newcommand\RW{ W}\)
\( \newcommand\RX{ X}\)
\( \newcommand\RY{ Y}\)
\( \newcommand\RZ{ Z}\)
\( \newcommand\Ra{ a}\)
\( \newcommand\Rb{ b}\)
\( \newcommand\Rc{ c}\)
\( \newcommand\Rd{ d}\)
\( \newcommand\Re{ e}\)
\( \newcommand\Rf{ f}\)
\( \newcommand\Rg{ g}\)
\( \newcommand\Rh{ h}\)
\( \newcommand\Ri{ i}\)
\( \newcommand\Rj{ j}\)
\( \newcommand\Rk{ k}\)
\( \newcommand\Rl{ l}\)
\( \newcommand { m}\)
\( \newcommand\Rn{ n}\)
\( \newcommand\Ro{ o}\)
\( \newcommand\Rp{ p}\)
\( \newcommand\Rq{ q}\)
\( \newcommand\Rr{ r}\)
\( \newcommand\Rs{ s}\)
\( \newcommand\Rt{ t}\)
\( \newcommand\Ru{ u}\)
\( \newcommand\Rv{ v}\)
\( \newcommand\Rw{ w}\)
\( \newcommand\Rx{ x}\)
\( \newcommand\Ry{ y}\)
\( \newcommand\Rz{ z}\)
\( \newcommand\BBA{\boldsymbol\RA}\)
\( \newcommand\BBB{\boldsymbol\RB}\)
\( \newcommand\BBC{\boldsymbol\RC}\)
\( \newcommand\BBD{\boldsymbol\RD}\)
\( \newcommand\BBE{\boldsymbol\RE}\)
\( \newcommand\BBF{\boldsymbol\RF}\)
\( \newcommand\BBG{\boldsymbol\RG}\)
\( \newcommand\BBH{\boldsymbol\RH}\)
\( \newcommand\BBI{\boldsymbol\RI}\)
\( \newcommand\BBJ{\boldsymbol\RJ}\)
\( \newcommand\BBK{\boldsymbol\RK}\)
\( \newcommand\BBL{\boldsymbol\RL}\)
\( \newcommand\BBM{\boldsymbol }\)
\( \newcommand\BBN{\boldsymbol\RN}\)
\( \newcommand\BBO{\boldsymbol\RO}\)
\( \newcommand\BBP{\boldsymbol\RP}\)
\( \newcommand\BBQ{\boldsymbol\RQ}\)
\( \newcommand\BBR{\boldsymbol\RR}\)
\( \newcommand\BBS{\boldsymbol\RS}\)
\( \newcommand\BBT{\boldsymbol\RT}\)
\( \newcommand\BBU{\boldsymbol\RU}\)
\( \newcommand\BBV{\boldsymbol\RV}\)
\( \newcommand\BBW{\boldsymbol\RW}\)
\( \newcommand\BBX{\boldsymbol\RX}\)
\( \newcommand\BBY{\boldsymbol\RY}\)
\( \newcommand\BBZ{\boldsymbol\RZ}\)
\( \newcommand\BBa{\boldsymbol\Ra}\)
\( \newcommand\BBb{\boldsymbol\Rb}\)
\( \newcommand\BBc{\boldsymbol\Rc}\)
\( \newcommand\BBd{\boldsymbol\Rd}\)
\( \newcommand\BBe{\boldsymbol\Re}\)
\( \newcommand\BBf{\boldsymbol\Rf}\)
\( \newcommand\BBg{\boldsymbol\Rg}\)
\( \newcommand\BBh{\boldsymbol\Rh}\}\)
\( \newcommand\BBi{\boldsymbol\Ri}\)
\( \newcommand\BBj{\boldsymbol\Rj}\)
\( \newcommand\BBk{\boldsymbol\Rk}\)
\( \newcommand\BBl{boldsymbol\Rl}\)
\( \newcommand\BBm{\boldsymbol }\)
\( \newcommand\BBn{\boldsymbol\Rn}\)
\( \newcommand\BBo{\boldsymbol\Ro}\)
\( \newcommand\BBp{\boldsymbol\Rp}\)
\( \newcommand\BBq{\boldsymbol\Rq}\)
\( \newcommand\BBr{\boldsymbol\Rr}\)
\( \newcommand\BBs{\boldsymbol\Rs}\)
\( \newcommand\BBt{\boldsymbol\Rt}\)
\( \newcommand\BBu{\boldsymbol\Ru}\)
\( \newcommand\BBv{\boldsymbol\Rv}\)
\( \newcommand\BBw{\boldsymbol\Rw}\)
\( \newcommand\BBx{\boldsymbol\Rx}\)
\( \newcommand\BBy{\boldsymbol\Ry}\)
\( \newcommand\BBz{\boldsymbol\Rz}\)
\( \newcommand\tcb{\textcolor{blue}\)
\( \newcommand\tcr{\textcolor{red}\)
\( \newcommand\bnabla{\boldsymbol{\nabla}}\)
\( \newcommand\Bell{\boldsymbol\ell}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \newcommand\ns{^\vphantom{*}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\impi{\int\limits_{-\infty}^{\infty}\!\!}\)
\( \newcommand\izpi{\int\limits_{0}^{\infty}\!\!}\)
\( \newcommand\etc{\it etc.\/}\)
\( \newcommand\etal{\it et al.\/}\)
\( \newcommand\opcit{\it op. cit.\/}\)
\( \newcommand\ie{\it i.e.\/}\)
\( \newcommand\Ie{\it I.e.\/}\)
\( \newcommand\viz{\it viz.\/}\)
\( \newcommand\eg{\it e.g.\/}\)
\( \newcommand\Eg{\it E.g.\/}\)
\( \newcommand\dbar{\,{\mathchar'26\mkern-12mu d}} \)
\( \def\sss#1{\scriptscriptstyle #1}\)
\( \def\ss#1{\scriptstyle #1}\)
\( \def\ssr#1{\scriptstyle #1}\)
\( \def\ssf#1{\scriptstyle #1}\)
\( \newcommand\NA{N_{\ssr{\!A}}}\)
\( \newcommand\lala{\langle\!\langle}\)
\( \newcommand\rara{\rangle\!\rangle}\)
\( \newcommand\blan{\big\langle}\)
\( \newcommand\bran{\big\rangle}\)
\( \newcommand\Blan{\Big\langle}\)
\( \newcommand\Bran{\Big\rangle}\)
\( \newcommand\intl{\int\limits}\)
\( \newcommand\half{\frac{1}{2}}\)
\( \newcommand\third{\frac{1}{3}}\)
\( \newcommand\fourth{\frac{1}{4}}\)
\( \newcommand\eighth{\frac{1}{8}}\)
\( \newcommand\uar{\uparrow}\)
\( \newcommand\dar{\downarrow}\)
\( \newcommand\undertext#1{$\underline{\hbox{#1}}$}\)
\( \newcommand\Tra{\mathop{\textsf{Tr}}\,}\)
\( \newcommand\det{\mathop{\textsf{det}}\,}\)
\( \def\tket#1{|  #1 \rangle}\)
\( \def\tbra#1{\langle #1|}\)
\( \def\tbraket#1#2{\langle #1  |   #2 \rangle}\)
\( \def\texpect#1#2#3{\langle #1 |   #2  |  #3 \rangle}\)
\( \def\sket#1{|  \, #1 \,  \rangle}\)
\( \def\sbra#1{\langle \,  #1 \, |}\)
\( \def\sbraket#1#2{\langle \, #1  \, |  \, #2 \,  \rangle}\)
\( \def\sexpect#1#2#3{\langle \, #1 \, | \,  #2  \, | \, #3 \, \rangle}\)
\(\def\ket#1{\big| \, #1\, \big\rangle}\)
\( \def\bra#1{\big\langle \, #1 \, \big|}\)
\( \def\braket#1#2{\big\langle \, #1\, \big| \,#2 \,\big\rangle}\)
\( \def\expect#1#2#3{\big\langle\, #1\, \big|\, #2\, \big| \,#3\, \big\rangle}\)
\( \newcommand\pz{\partial}\)
\( \newcommand\pzb{\bar{\partial}}\)
\( \newcommand\svph{\vphantom{\int}}\)
\( \newcommand\vph{\vphantom{\sum_i}}\)
\( \newcommand\bvph{\vphantom{\sum_N^N}}\)
\( \newcommand\nd{^{\vphantom{\dagger}}}\)
\( \newcommand\ns{^{\vphantom{*}}}\)
\( \newcommand\yd{^\dagger}\)
\( \newcommand\zb{\bar z}\)
\( \newcommand\zdot{\dot z}\)
\( \newcommand\zbdot{\dot{\bar z}}\)
\( \newcommand\kB{k_{\sss{B}}}\)
\( \newcommand\kT{k_{\sss{B}}T}\)
\( \newcommand\gtau{g_\tau}\)
\( \newcommand\Htil{\tilde H}\)
\( \newcommand\pairo{(\phi\nd_0,J\nd_0)}\)
\( \newcommand\pairm{(\phi\nd_0,J)}\)
\( \newcommand\pairob{(\Bphi\nd_0,\BJ\nd_0)}\)
\( \newcommand\pairmb{(\Bphi\nd_0,\BJ)}\)
\( \newcommand\pair{(\phi,J)}\)
\( \newcommand\Hz{H\nd_0}\)
\( \newcommand\Ho{H\nd_1}\)
\( \newcommand\Htz{\Htil\nd_0}\)
\( \newcommand\Hto{\Htil\nd_1}\)
\( \newcommand\oc{\omega_\Rc}\)

\(\newcommand \gtwid{\approx}\)

\( \newcommand\index{\textsf{ind}}\)
\( \newcommand\csch{\,{ csch\,}}\)
\( \newcommand\ctnh{\,{ ctnh\,}}\)
\( \newcommand\ctn{\,{ ctn\,}}\)
\( \newcommand\sgn{\,{ sgn\,}}\)
\( \def\tmapright#1{\xrightarrow \limits^{#1}}\)
\( \def\bmapright#1{\xrightarrow\limits_{#1}}\)
\( \newcommand\hfb{\hfill\break}\)
\( \newcommand\Rep{\textsf{Re}\,}\)
\( \newcommand\Imp{\textsf{Im}\,}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \def\tmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits^{#1}}\ }\)
\( \def\bmapright#1{ \smash{\mathop{\hbox to 35pt{\rightarrowfill}}\limits_{#1}}\ }\)
\( \newcommand\bsqcap{\mbox{\boldmath{$\sqcap$}}}\)

\( \def\pabc#1#2#3{\left({\pz #1\over\pz #2}\right)\ns_{\!\!#3}}\)
\( \def\spabc#1#2#3{\big({\pz #1\over\pz #2}\big)\ns_{\!#3}}\)
\( \def\qabc#1#2#3{\pz^2\! #1\over\pz #2\,\pz #3}\)
\( \def\rabc#1#2#3#4{(\pz #1,\pz #2)\over (\pz #3,\pz #4)}\)
\( \newcommand\subA{\ns_\ssr{A}}\)
\( \newcommand\subB{\ns_\ssr{B}}\)
\( \newcommand\subC{\ns_\ssr{C}}\)
\( \newcommand\subD{\ns_\ssr{D}}\)
\( \newcommand\subAB{\ns_\ssr{AB}}\)
\( \newcommand\subBC{\ns_\ssr{BC}}\)
\( \newcommand\subCD{\ns_\ssr{CD}}\)
\( \newcommand\subDA{\ns_\ssr{DA}}\)
\( \def\lmapright#1{\ \ \smash{\mathop{\hbox to 55pt{\rightarrowfill}}\limits^{#1}}\ \ }\)
\( \def\enth#1{\RDelta {\textsf H}^0_\Rf[{ #1}]}\)
\( \newcommand\longrightleftharpoons{ \mathop{\vcenter{\hbox{\ooalign{\raise1pt\hbox{$\longrightharpoonup\joinrel$}\crcr  \lower1pt\hbox{$\longleftharpoondown\joinrel$}}}}}}\)
\( \newcommand\longrightharpoonup{\relbar\joinrel\rightharpoonup}\)
\( \newcommand\longleftharpoondown{\leftharpoondown\joinrel\relbar}\)
\( \newcommand\cds{\,\bullet\,}\)
\( \newcommand\ccs{\,\circ\,}\)
\( \newcommand\nsub{_{\vphantom{\dagger}}}\)
\( \newcommand\rhohat{\hat\rho}\)
\( \newcommand\vrhhat{\hat\vrh}\)
\( \newcommand\impi{\int\limits_{-\infty}^\infty\!\!\!}\)
\( \newcommand\brangle{\big\rangle}\)
\( \newcommand\blangle{\big\langle}\)
\( \newcommand\vet{\tilde\ve}\)
\( \newcommand\zbar{\bar z}\)
\( \newcommand\ftil{\tilde f}\)
\( \newcommand\XBE{\RXi\ns_\ssr{BE}}\)
\( \newcommand\XFD{\RXi\ns_\ssr{FD}}\)
\( \newcommand\OBE{\Omega\ns_\ssr{BE}}\)
\( \newcommand\OFD{\Omega\ns_\ssr{FD}}\)
\( \newcommand\veF{\ve\ns_\RF}\)
\( \newcommand\kF{k\ns_\RF}\)
\( \newcommand\kFu{k\ns_{\RF\uar}}\)
\( \newcommand\SZ{\textsf Z}}\) \( \newcommand\kFd{k\ns_{\RF\dar}\)
\( \newcommand\muB{\mu\ns_\ssr{B}}\)
\( \newcommand\mutB{\tilde\mu}\ns_\ssr{B}\)
\( \newcommand\xoN{\Bx\ns_1\,,\,\ldots\,,\,\Bx\ns_N}\)
\( \newcommand\rok{\Br\ns_1\,,\,\ldots\,,\,\Br\ns_k}\)
\( \newcommand\xhiOZ{\xhi^\ssr{OZ}}\)
\( \newcommand\xhihOZ

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[1], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\jhz{\HJ(0)}\)
\( \newcommand\nda{\nd_\alpha}\)
\( \newcommand\ndap{\nd_{\alpha'}}\)
\( \newcommand\labar

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Template:MathJaxArovas), /content/body/div/span[2], line 1, column 1
    at template()
    at (Bookshelves/Thermodynamics_and_Statistical_Mechanics/Book:_Thermodynamics_and_Statistical_Mechanics_(Arovas)/08:_Nonequilibrium_Phenomena/8.04:_Relaxation_Time_Approximation), /content/body/p/span, line 1, column 23

\)
\( \newcommand\msa{m\ns_\ssr{A}}\)
\( \newcommand\msb{m\ns_\ssr{B}}\)
\( \newcommand\mss{m\ns_\Rs}\)
\( \newcommand\HBx{\hat\Bx}\)
\( \newcommand\HBy{\hat\By}\)
\( \newcommand\HBz{\hat\Bz}\)
\( \newcommand\thm{\theta\ns_m}\)
\( \newcommand\thp{\theta\ns_\phi}\)
\( \newcommand\mtil{\widetilde m}\)
\( \newcommand\phitil{\widetilde\phi}\)
\( \newcommand\delf{\delta\! f}\)
\( \newcommand\coll{\bigg({\pz f\over\pz t}\bigg)\nd_{\! coll}}\)
\( \newcommand\stre{\bigg({\pz f\over\pz t}\bigg)\nd_{\! str}}\)
\( \newcommand\idrp{\int\!\!{d^3\!r\,d^3\!p\over h^3}\>}\)
\( \newcommand\vbar{\bar v}\)
\( \newcommand\BCE{\mbox{\boldmath{$\CE$}}\!}\)
\( \newcommand\BCR{\mbox{\boldmath{$\CR$}}\!}\)
\( \newcommand\gla{g\nd_{\RLambda\nd}}\)
\( \newcommand\TA{T\ns_\ssr{A}}\)
\( \newcommand\TB{T\ns_\ssr{B}}\)
\( \newcommand\ncdot{\!\cdot\!}\)
\( \newcommand\NS{N\ns_{\textsf S}}\)

Approximation of Collision Integral

We now consider a very simple model of the collision integral,

\[\coll=-\,{f-f^0\over\tau}=-{\delf\over\tau}\ .\]

This model is known as the relaxation time approximation. Here, \(f^0=f^0(\Br,\Bp,t)\) is a distribution function which describes a local equilibrium at each position \(\Br\) and time \(t\). The quantity \(\tau\) is the relaxation time, which can in principle be momentum-dependent, but which we shall first consider to be constant. In the absence of streaming terms, we have

\[{\pz \,\delf\over\pz t}=-{\delf\over\tau} \qquad\Longrightarrow\qquad \delf(\Br,\Bp,t)=\delf(\Br,\Bp,0)\,e^{-t/\tau}\ .\]

The distribution \(f\) then relaxes to the equilibrium distribution \(f^0\) on a time scale \(\tau\). We note that this approximation is obviously flawed in that all quantities – even the collisional invariants – relax to their equilibrium values on the scale \(\tau\). In the Appendix, we consider a model for the collision integral in which the collisional invariants are all preserved, but everything else relaxes to local equilibrium at a single rate.

Computation of the scattering time

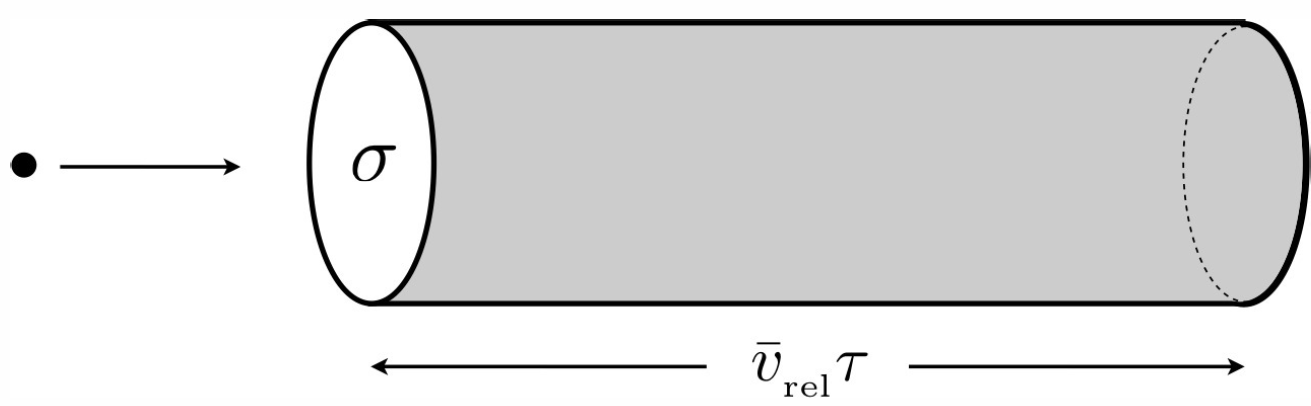
Consider two particles with velocities \(\Bv\) and \(\Bv'\). The average of their relative speed is

\[\langle \,|\Bv-\Bv'|\, \rangle = \int\!\!d^3\!v\!\int\!\!d^3\!v'\>P(\Bv)\,P(\Bv')\,|\Bv-\Bv'|\ ,\]

where \(P(\Bv)\) is the Maxwell velocity distribution,

\[P(\Bv)=\bigg({m\over 2\pi\kT}\bigg)^{\!\!3/2}\exp\bigg(\!-\!{m\Bv^2\over 2\kT}\bigg)\ ,\]

which follows from the Boltzmann form of the equilibrium distribution \(f^0(\Bp)\). It is left as an exercise for the student to verify that

\[{\bar v}\ns_{rel} \equiv \langle \,|\Bv-\Bv'|\, \rangle= {4\over \sqrt{\pi}}\,\bigg({\kT\over m}\bigg)^{\!\!1/2}\ .\]

Note that \({\bar v}\ns_{rel} = \sqrt{2} \,{\bar v}\), where \({\bar v}\) is the average particle speed. Let \(\sigma\) be the total scattering cross section, which for hard spheres is \(\sigma=\pi d^2\), where \(d\) is the hard sphere diameter. Then the rate at which particles scatter is

\[{1\over\tau}=n\, {\bar v}\ns_{rel}\, \sigma\ . \label{nutaueqn}\]

The particle mean free path is simply

\[\ell={\bar v}\,\tau={1\over\sqrt{2}\,n\,\sigma}\ .\]

While the scattering length is not temperature-dependent within this formalism, the scattering time is \(T\)-dependent, with

\[\tau(T)={1\over n\,{\bar v}\ns_{rel} \, \sigma} = {\sqrt{\pi}\over 4 n\sigma}\bigg({m\over\kT}\bigg)^{\!\!1/2}\ .\]

As \(T\to 0\), the collision time diverges as \(\tau\propto T^{-1/2}\), because the particles on average move more slowly at lower temperatures. The mean free path, however, is independent of \(T\), and is given by \(\ell=1/\sqrt{2}n\sigma\).

Figure \(\PageIndex{1}\): Graphic representation of the equation \(n\,\sigma\,{\bar v}_{rel}\,\tau=1\), which yields the scattering time \(\tau\) in terms of the number density \(n\), average particle pair relative velocity \({\bar v}_{rel}\), and two-particle total scattering cross section \(\sigma\). The equation says that on average there must be one particle within the tube.

Thermal conductivity

We consider a system with a temperature gradient \(\bnabla T\) and seek a steady state ( time-independent) solution to the Boltzmann equation. We assume \(F\ns_\alpha=\CQ\ns_{\alpha\beta}=0\). Appealing to Equation \ref{bwig}, and using the relaxation time approximation for the collision integral, we have

\[\delta \!f=-{\tau (\ve-c\ns_p\,T)\over\kB T^2}\,(\Bv\cdot\bnabla T)\,f^0\ .\]

We are now ready to compute the energy and particle currents. In order to compute the local density of any quantity \(A(\Br,\Bp)\), we multiply by the distribution \(f(\Br,\Bp)\) and integrate over momentum:

\[\rho\nd_{\!A\nd}(\Br,t)=\int\!\! d^3\!p \,A(\Br,\Bp)\,f(\Br,\Bp,t)\ ,\]

For the energy (thermal) current, we let \(A= \ve\, v\ns_\alpha=\ve\,p\ns_\alpha/m\), in which case \(\rho\nd_{\!A\nd}=j\ns_\alpha\). Note that \(\int\!\!d^3\!p\>\Bp\,f^0=0\) since \(f^0\) is isotropic in \(\Bp\) even when \(\mu\) and \(T\) depend on \(\Br\). Thus, only \(\delf\) enters into the calculation of the various currents. Thus, the energy (thermal) current is

\[\begin{split} j^\alpha_\ve(\Br)&=\int\!\! d^3\!p \> \ve\,v^\alpha\,\delf\\ &=-{n\tau\over\kB T^2}\, \blangle \, v^\alpha v^\beta \,\ve\,(\ve-c\ns_p\,T) \, \brangle\,{\pz T\over\pz x^\beta}\ , \label{jtheqn} \end{split}\]

where the repeated index \(\beta\) is summed over, and where momentum averages are defined relative to the equilibrium distribution,

\[\langle \, \phi(\Bp) \, \rangle = \int\!\! d^3\!p \,\phi(\Bp)\,f^0(\Bp)\bigg/\!\!\int\!\! d^3\!p \,f^0(\Bp) =\!\!\int\!\!d^3\!v\>P(\Bv)\,\phi(m\Bv)\ .\]

In this context, it is useful to point out the identity

\[d^3\!p \,f^0(\Bp)=n\,d^3\!v\>P(\Bv)\ ,\]

where

\[P(\Bv)=\bigg({m\over 2\pi\kT}\bigg)^{\!3/2}\>e^{-m(\Bv-\BV)^2/2\kT}\]

is the Maxwell velocity distribution.

Note that if \(\phi=\phi(\ve)\) is a function of the energy, and if \(\BV=0\), then

\[d^3\!p \,f^0(\Bp)=n\,d^3\!v\>P(\Bv)=n\,{\widetilde P}(\ve)\,d\ve\ ,\]

where

\[{\widetilde P}(\ve)=\frac{2}{\sqrt{\pi}} (\kT)^{-3/2}\,\ve^{1/2}\,e^{-\ve/\kT}\ ,\]

is the Maxwellian distribution of single particle energies. This distribution is normalized with \(\int\limits_0^\infty\!d\ve\,{\widetilde P}(\ve)=1\). Averages with respect to this distribution are given by

\[\langle\,\phi(\ve)\,\rangle=\int\limits_0^\infty\!\!d\ve\>\phi(\ve)\,{\widetilde P}(\ve) =\frac{2}{\sqrt{\pi}} (\kT)^{-3/2}\!\!\int\limits_0^\infty\!\!d\ve\>\ve^{1/2}\,\phi(\ve)\,e^{-\ve/\kT}\ .\]

If \(\phi(\ve)\) is homogeneous, then for any \(\alpha\) we have

\[\langle\,\ve^\alpha\,\rangle=\frac{2}{\sqrt{\pi}}\RGamma\big(\alpha+\frac{3}{2}\big) (\kT)^\alpha\ .\]

Due to spatial isotropy, it is clear that we can replace

\[v^\alpha\,v^\beta \to \third\Bv^2\,\delta\ns_{\alpha\beta} = {2\ve\over 3m}\,\delta\ns_{\alpha\beta}\]

in Equation \ref{jtheqn}. We then have \(\Bj\ns_\ve=-\kappa\,\bnabla T\), with

\[\kappa={2n\tau\over 3m\kB T^2}\,\langle\, \ve^2\big(\ve-c\ns_p\,T\big)\,\rangle = 5n\tau \dfrac{\kB^2 T}{ 2m}=\frac{\pi}{8} n\ell{\bar v}\,c\ns_p\ ,\]

where we have used \(c \ns_p =\frac{5}{2}\kB\) and \(\vbar^2=\frac{8k_{B}T}{\pi m}\). The quantity \(\kappa\) is called the thermal conductivity. Note that \(\kappa\propto T^{1/2}\).

Viscosity

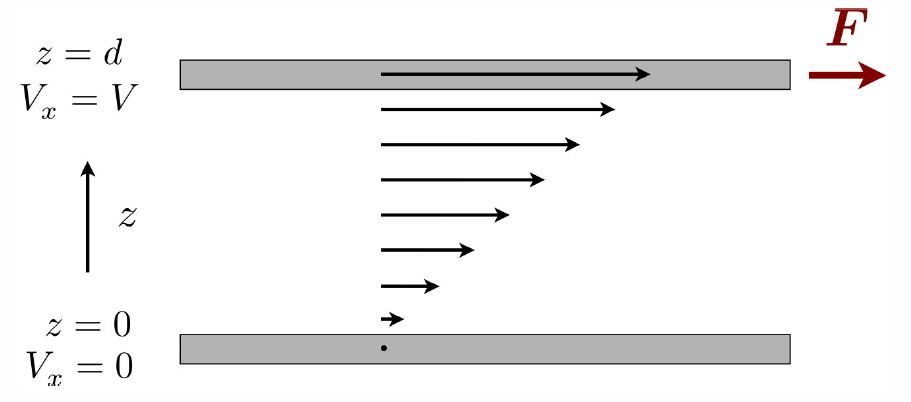
Consider the situation depicted in Figure \(\PageIndex{2}\). A fluid filling the space between two large flat plates at \(z=0\) and \(z=d\) is set in motion by a force \(\BF=F\HBx\) applied to the upper plate; the lower plate is fixed. It is assumed that the fluid’s velocity locally matches that of the plates. Fluid particles at the top have an average \(x\)-component of their momentum \(\langle p\ns_x\rangle=mV\). As these particles move downward toward lower \(z\) values, they bring their \(x\)-momenta with them. Therefore there is a downward (\(-\zhat\)-directed) flow of \(\langle p\ns_x\rangle\). Since \(x\)-momentum is constantly being drawn away from \(z=d\) plane, this means that there is a \(-\Bx\)-directed viscous drag on the upper plate. The viscous drag force per unit area is given by \(F\ns_{drag}/A=-\eta V/d\), where \(V/d=\pz V\ns_x/\pz z\) is the velocity gradient and \(\eta\) is the shear viscosity. In steady state, the applied force balances the drag force, \(F+F\ns_{drag}=0\). Clearly in the steady state the net momentum density of the fluid does not change, and is given by \(\half\rho V\HBx\), where \(\rho\) is the fluid mass density. The momentum per unit time injected into the fluid by the upper plate at \(z=d\) is then extracted by the lower plate at \(z=0\). The momentum flux density \(\RPi\ns_{xz}=n\,\langle\,p\ns_x\,v\ns_z\,\rangle\) is the drag force on the upper surface per unit area: \(\RPi\ns_{xz}=-\eta\,{\pz V\ns_x\over\pz z}\). The units of viscosity are \([\eta]=M/LT\).

We now provide some formal definitions of viscosity. As we shall see presently, there is in fact a second type of viscosity, called second viscosity or bulk viscosity, which is measurable although not by the type of experiment depicted in igure \(\PageIndex{2}\).

The momentum flux tensor \(\RPi\ns_{\alpha\beta}=n\,\langle\,p\ns_\alpha\,v\ns_\beta\,\rangle\) is defined to be the current of momentum component \(p\ns_\alpha\) in the direction of increasing \(x\ns_\beta\). For a gas in motion with average velocity \(\BV\!\), we have

\[\begin{split} \RPi\ns_{\alpha\beta}&=nm\,\langle\,(V\ns_\alpha+v'_\alpha)(V\ns_\beta+v'_\beta)\,\rangle\\ &=nm\, V\ns_\alpha V\ns_\beta + nm\,\langle\,v'_\alpha v'_\beta\,\rangle\\ &=nm\, V\ns_\alpha V\ns_\beta+\third nm\,\langle\,{\Bv'}^2\,\rangle\,\delta\ns_{\alpha\beta}\\ &=\rho\, V\ns_\alpha V\ns_\beta+p\,\delta\ns_{\alpha\beta}\ , \end{split}\]

where \(\Bv'\) is the particle velocity in a frame moving with velocity \(\BV\!\), and where we have invoked the ideal gas law \(p=n\kT\). The mass density is \(\rho=nm\).

Figure \(\PageIndex{2}\): Gedankenexperiment to measure shear viscosity \(\eta\) in a fluid. The lower plate is fixed. The viscous drag force per unit area on the upper plate is \(F_{drag}/A=-\eta V/d\). This must be balanced by an applied force \(F\).

When \(\BV\) is spatially varying,

\[\RPi\ns_{\alpha\beta}=p\,\delta\ns_{\alpha\beta} + \rho\, V\ns_\alpha V\ns_\beta -{\tilde\sigma}_{\alpha\beta}\ ,\]

where \({\tilde\sigma}\ns_{\alpha\beta}\) is the viscosity stress tensor. Any symmetric tensor, such as \({\tilde\sigma}\ns_{\alpha\beta}\), can be decomposed into a sum of (i) a traceless component, and (ii) a component proportional to the identity matrix. Since \({\tilde\sigma}\ns_{\alpha\beta}\) should be, to first order, linear in the spatial derivatives of the components of the velocity field \(\BV\), there is a unique two-parameter decomposition:

\[\begin{split} {\tilde\sigma}_{\alpha\beta}&=\eta\Bigg( {\pz V\ns_\alpha\over\pz x\ns_\beta} + {\pz V\ns_\beta\over\pz x\ns_\alpha} -\frac{2}{3}\,\bnabla\!\cdot\!\BV\,\delta\ns_{\alpha\beta}\bigg) +\zeta\,\bnabla\!\cdot\!\BV\,\delta\ns_{\alpha\beta}\\ &=2\eta\,\Big(\CQ\ns_{\alpha\beta}-\third\Tra(\CQ)\,\delta\ns_{\alpha\beta}\Big) + \zeta\,\Tra(\CQ)\,\delta\ns_{\alpha\beta}\ . \end{split}\]

The coefficient of the traceless component is \(\eta\), known as the shear viscosity. The coefficient of the component proportional to the identity is \(\zeta\), known as the bulk viscosity. The full stress tensor \(\sigma\ns_{\alpha\beta}\) contains a contribution from the pressure:

\[\sigma\ns_{\alpha\beta}=-p\,\delta\ns_{\alpha\beta} + {\tilde\sigma}\ns_{\alpha\beta}\ .\]

The differential force \(dF\ns_\alpha\) that a fluid exerts on on a surface element \(\nhat\,dA\) is

\[dF\ns_\alpha=-\sigma\ns_{\alpha\beta}\,n\ns_\beta\,dA\ ,\]

where we are using the Einstein summation convention and summing over the repeated index \(\beta\). We will now compute the shear viscosity \(\eta\) using the Boltzmann equation in the relaxation time approximation.

Appealing again to Equation \ref{bwig}, with \(\BF=0\) and \(h=c\ns_p T\), we find

\[\delf=-{\tau\over\kT}\Bigg\{ m\, v\ns_\alpha v\ns_\beta\,\CQ\ns_{\alpha\beta} +{\ve-c\ns_p\,T\over T}\>\Bv\cdot\bnabla T -{\ve\over c\ns_V/\kB}\,\bnabla\ncdot\BV\Bigg\}\>f^0\ .\]

We assume \(\bnabla T=\bnabla\ncdot\BV=0\), and we compute the momentum flux:

\[\begin{split} \RPi\ns_{xz}&=n\!\int\!\! d^3\!p \> p\ns_x v\ns_z\,\delf\\ &=-{nm^2\tau \over \kT}\>\CQ\ns_{\alpha\beta} \>\langle\,v\ns_x\,v\ns_z\,v\ns_\alpha\,v\ns_\beta\,\rangle\\ &=-{n\tau\over\kT}\bigg({\pz V\ns_x\over\pz z} + {\pz V\ns_z\over\pz x}\bigg) \, \langle\, mv_x^2\cdot mv_z^2\,\rangle\\ &=-n\tau\kT \bigg({\pz V\ns_z\over\pz x} + {\pz V\ns_x\over\pz z}\bigg)\ . \end{split}\]

Thus, if \(V\ns_x=V\ns_x(z)\), we have

\[\RPi\ns_{xz}=-n\tau \kT\,{\pz V\ns_x\over\pz z}\]

from which we read off the viscosity,

\[\eta= n\kT\tau=\frac{\pi}{8} nm\ell{\bar v} \ .\]

Note that \(\eta(T)\propto T^{1/2}\).

Figure \(\PageIndex{3}\): Left: thermal conductivity (\(\lambda\) in figure) of Ar between \(T=800\,\RK\) and \(T=2600\,\RK\). The best fit to a single power law \(\lambda=aT^b\) results in \(b=0.651\). Source: G. S. Springer and E. W. Wingeier, J. Chem Phys. 59, 1747 (1972). Right: log-log plot of shear viscosity (\(\mu\) in figure) of He between \(T\approx 15\,\RK\) and \(T\approx 1000\,\RK\). The red line has slope \(\half\). The slope of the data is approximately \(0.633\). Source: J. Kestin and W. Leidenfrost, Physica 25, 537 (1959).

How well do these predictions hold up? In igure \(\PageIndex{3}\), we plot data for the thermal conductivity of argon and the shear viscosity of helium. Both show a clear sublinear behavior as a function of temperature, but the slope \(d\ln\kappa/d\ln T\) is approximately \(0.65\) and \(d\ln\eta/d\ln T\) is approximately \(0.63\). Clearly the simple model is not even getting the functional dependence on \(T\) right, let alone its coefficient. Still, our crude theory is at least qualitatively correct.

Why do both \(\kappa(T)\) as well as \(\eta(T)\) decrease at low temperatures? The reason is that the heat current which flows in response to \(\bnabla T\) as well as the momentum current which flows in response to \(\pz V\ns_x/\pz z\) are due to the presence of collisions, which result in momentum and energy transfer between particles. This is true even when total energy and momentum are conserved, which they are not in the relaxation time approximation. Intuitively, we might think that the viscosity should increase as the temperature is lowered, since common experience tells us that fluids ‘gum up’ as they get colder – think of honey as an extreme example. But of course honey is nothing like an ideal gas, and the physics behind the crystallization or glass transition which occurs in real fluids when they get sufficiently cold is completely absent from our approach. In our calculation, viscosity results from collisions, and with no collisions there is no momentum transfer and hence no viscosity. If, for example, the gas particles were to simply pass through each other, as though they were ghosts, then there would be no opposition to maintaining an arbitrary velocity gradient.

Oscillating External Force

Suppose a uniform oscillating external force \(\BF\ns_{ext}(t)=\BF\,e^{-i\omega t}\) is applied. For a system of charged particles, this force would arise from an external electric field \(\BF\ns_{ext}=q\BE\,e^{-i\omega t}\), where \(q\) is the charge of each particle. We’ll assume \(\bnabla T=0\). The Boltzmann equation is then written

\[{\pz f\over\pz t}+{\Bp\over m}\cdot{\pz f\over\pz \Br} +\BF e^{-i\omega t}\cdot{\pz f\over\pz\Bp}= -{f-f^0\over \tau}\ .\]

We again write \(f=f^0+\delf\), and we assume \(\delf\) is spatially constant. Thus,

\[{\pz\,\delf\over\pz t} + \BF e^{-i\omega t}\cdot\Bv\,{\pz f^0\over\pz\ve} = -{\delf\over\tau}\ .\]

If we assume \(\delf(t)=\delf(\omega)\,e^{-i\omega t}\) then the above differential equation is converted to an algebraic equation, with solution

\[\delf(t)=-{\tau\,e^{-i\omega t}\over 1-i\omega \tau}\>{\pz f^0\over\pz\ve}\>\BF\cdot\Bv\ .\]

We now compute the particle current:

\[\begin{split} j\ns_\alpha(\Br,t)&=\int\!\! d^3\!p \>\Bv\>\delf\\ &={\tau\,e^{-i\omega t}\over 1-i\omega \tau}\cdot{F\ns_\beta\over\kT}\!\!\int\!\! d^3\!p \>f^0(\Bp)\,v\ns_\alpha\,v\ns_\beta\bvph\\ &={\tau\,e^{-i\omega t}\over 1-i\omega \tau}\cdot{n F\ns_\alpha\over 3\kT}\!\!\int\!\!d^3\!v\>P(\Bv)\,\Bv^2\bvph\\ &={n\tau\over m}\cdot{F\ns_\alpha\,e^{-i\omega t}\over 1-i\omega \tau}\ . \end{split}\]

If the particles are electrons, with charge \(q=-e\), then the electrical current is \((-e)\) times the particle current. We then obtain

\[j^\ssr{(elec)}_\alpha(t)={ne^2\tau\over m}\cdot {E\ns_\alpha\,e^{-i\omega t}\over 1-i\omega \tau}\equiv\sigma\ns_{\alpha\beta}(\omega) \>E\ns_\beta\,e^{-i\omega t}\ ,\]

where

\[\sigma\ns_{\alpha\beta}(\omega)={ne^2\tau\over m}\cdot{1\over 1-i\omega\tau}\,\delta\ns_{\alpha\beta}\]

is the frequency-dependent electrical conductivity tensor. Of course for fermions such as electrons, we should be using the Fermi distribution in place of the Maxwell-Boltzmann distribution for \(f^0(\Bp)\). This affects the relation between \(n\) and \(\mu\) only, and the final result for the conductivity tensor \(\sigma\ns_{\alpha\beta}(\omega)\) is unchanged.

Quick and Dirty Treatment of Transport

Suppose we have some averaged intensive quantity \(\phi\) which is spatially dependent through \(T(\Br)\) or \(\mu(\Br)\) or \(\BV(\Br)\). For simplicity we will write \(\phi=\phi(z)\). We wish to compute the current of \(\phi\) across some surface whose equation is \(dz=0\). If the mean free path is \(\ell\), then the value of \(\phi\) for particles crossing this surface in the \(+\zhat\) direction is \(\phi(z-\ell\cos\theta)\), where \(\theta\) is the angle the particle’s velocity makes with respect to \(\zhat\), \(\cos\theta=v\ns_z/v\). We perform the same analysis for particles moving in the \(-\zhat\) direction, for which \(\phi=\phi(z+\ell\cos\theta)\). The current of \(\phi\) through this surface is then

\[\begin{split} \Bj\ns_\phi&=n\zhat\!\!\!\int\limits_{v\ns_z >0}\!\!\!\!d^3\!v\,P(\Bv)\,v\ns_z\,\phi(z-\ell\cos\theta) +n\zhat\!\!\!\int\limits_{v\ns_z<0}\!\!\!\!d^3\!v\,P(\Bv)\,v\ns_z\,\phi(z+\ell\cos\theta)\\ &=-n\ell\,{\pz\phi\over\pz z}\zhat\!\int\!\!d^3\!v\>P(\Bv)\,{v^2_z\over v}=-\third n{\bar v}\ell\,{\pz\phi\over\pz z}\,\zhat\ , \end{split}\]

where \({\bar v}=\sqrt{\frac{8k_{B}T}{\pi m}}\) is the average particle speed. If the \(z\)-dependence of \(\phi\) comes through the dependence of \(\phi\) on the local temperature \(T\), then we have

\[\Bj\ns_\phi=-\third\,n\ell{\bar v}\,{\pz\phi\over\pz T}\,\bnabla T \equiv -K\,\bnabla T\ ,\]

where

\[K=\third n\ell {\bar v}\,{\pz\phi\over\pz T}\]

is the transport coefficient. If \(\phi=\langle\ve\rangle\), then \(\frac{\pz\phi}{\pz T}=c\nd_p\), where \(c\nd_p\) is the heat capacity per particle at constant pressure. We then find \(\Bj\ns_\ve=-\kappa\,\bnabla T\) with thermal conductivity

\[\kappa=\third n\ell{\bar v}\, c\nd_p\ .\]

Our Boltzmann equation calculation yielded the same result, but with a prefactor of \(\frac{\pi}{8}\) instead of \(\third\).

We can make a similar argument for the viscosity. In this case \(\phi=\langle p\ns_x\rangle\) is spatially varying through its dependence on the flow velocity \(\BV(\Br)\). Clearly \(\pz\phi/\pz V\ns_x=m\), hence

\[j^z_{p\ns_x}=\RPi\ns_{xz}=-\third nm\ell{\bar v} \,{\pz V\ns_x\over\pz z}\ ,\]

from which we identify the viscosity, \(\eta=\third nm\ell {\bar v}\). Once again, this agrees in its functional dependences with the Boltzmann equation calculation in the relaxation time approximation. Only the coefficients differ. The ratio of the coefficients is \(K\ns_\ssr{QDC}/K\ns_\ssr{BRT}=\frac{8}{3\pi}=0.849\) in both cases⁶.

Thermal diffusivity, kinematic viscosity, and Prandtl number

Suppose, under conditions of constant pressure, we add heat \(q\) per unit volume to an ideal gas. We know from thermodynamics that its temperature will then increase by an amount \(\RDelta T=q/nc\ns_p\). If a heat current \(\Bj\ns_q\) flows, then the continuity equation for energy flow requires

\[nc\ns_p\,{\pz T\over\pz t} + \bnabla\cdot \Bj\ns_q=0\ .\]

In a system where there is no net particle current, the heat current \(\Bj\ns_q\) is the same as the energy current \(\Bj\ns_\ve\), and since \(\Bj\ns_\ve=-\kappa\,\bnabla T\), we obtain a diffusion equation for temperature,

\[{\pz T\over \pz t}={\kappa\over n c\ns_p}\,\nabla^2 T\ .\]

The combination

\[a\equiv {\kappa\over n c\ns_p}\]

is known as the thermal diffusivity. Our Boltzmann equation calculation in the relaxation time approximation yielded the result \(\kappa=n\kT\tau c\ns_p/m\). Thus, we find \(a=\kT\tau/m\) via this method. Note that the dimensions of \(a\) are the same as for any diffusion constant \(D\), namely \([a]=L^2/T\).

[Prandtl] Viscosities, thermal conductivities, and Prandtl numbers for some common gases at \(T=293\,\RK\) and \(p=1\,\)atm. (Source: Table 1.1 of Smith and Jensen, with data for triatomic gases added.)

Gas	\(\eta\) (\(\mu{Pa}\cdot\Rs\))	\(\kappa\) (\({mW}/\Rm\cdot\RK\))	\(c\ns_p/\kB\)	\({Pr}\)
He	\(19.5\)	\(149\)	\(2.50\)	\(0.682\)
Ar	\(22.3\)	\(17.4\)	\(2.50\)	\(0.666\)
Xe	\(22.7\)	\(5.46\)	\(2.50\)	\(0.659\)
\(\RH\ns_2\)	\(8.67\)	\(179\)	\(3.47\)	\(0.693\)
\(\RN\ns_2\)	\(17.6\)	\(25.5\)	\(3.53\)	\(0.721\)
\(\RO\ns_2\)	\(20.3\)	\(26.0\)	\(3.50\)	\(0.711\)
\(\RC\RH\ns_4\)	\(11.2\)	\(33.5\)	\(4.29\)	\(0.74\)
\(\RC\RO\ns_2\)	\(14.8\)	\(18.1\)	\(4.47\)	\(0.71\)
\(\RN\RH\ns_3\)	\(10.1\)	\(24.6\)	\(4.50\)	\(0.90\)

Another quantity with dimensions of \(L^2/T\) is the kinematic viscosity, \(\nu=\eta/\rho\), where \(\rho=nm\) is the mass density. We found \(\eta=n\kT\tau\) from the relaxation time approximation calculation, hence \(\nu=\kT\tau/m\). The ratio \(\nu/a\), called the Prandtl number, \({Pr}=\eta c\ns_p/m\kappa\), is dimensionless. According to our calculations, \({Pr}=1\). According to table [Prandtl], most monatomic gases have \({Pr}\approx\frac{2}{3}\).