9.6: Additional Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
9.1 Denaturation of DNA
(This problem is modified from one posed by M.E. Fisher. It deals with a research question born in the 1960s that is still of interest today: Douglas Poland and Harold A. Scheraga, “Occurrence of a phase transition in nucleic acid models,” J. Chem. Phys. 45 (1966) 1464–1469; M.E. Fisher, “Effect of excluded volume on phase transitions in biopolymers,” J. Chem. Phys. 45 (1966) 1469–1473; Yariv Kafri, David Mukamel, and Luca Peliti, “Why is the DNA denaturation transition first order?” Phys. Rev. Lett. 85 (2000) 4988–4991.)
The biological polymer DNA consists of two polymeric strands which, in their usual state, are twisted together to form a rather rigid double helix. However as the temperature is raised regions of the molecule may “melt”, breaking the weak bonds that hold the two strands together. In this case the two strands separate and coil randomly in the solution. If the entire molecule melts then the DNA is said to be “denatured”. A simple model to aid in understanding this phenomenon is the following.
Successive segments of the molecule are regarded as being in either the helical state or in the melted state. A segment in the helical state has a lower energy than one in the melted state (−\epsilon vs. 0) but a segment in the melted state has q different possible orientations (due to coiling) whereas a segment in the helical state has only one. However, the first or last segment of a run of melted segments has a smaller number of configurations, rq, where r can be as small as 10−3. (A melted segment that is both the first and last segment of a run is doubly restricted and has only r2q configurations.) Sample DNA configurations and their associated “Boltzmann factors” are shown below.
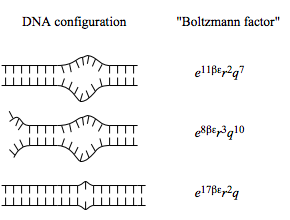
a. Introduce a variable hi for the ith segment such that
h_{i}=\left\{\begin{array}{ll}{1} & {\text { if the } i \text { th segment is helical }} \\ {0} & {\text { if the } i \text { th segment is melted. }}\end{array}\right.
Show that the canonical partition function for a molecule of N segments is
Z_{N}(T, \epsilon, r)=\sum_{h_{1}=0}^{1} \sum_{h_{2}=0}^{1} \cdots \sum_{h_{N}=0}^{1} \prod_{i=1}^{N} e^{\beta \epsilon h_{i}} q^{\left(1-h_{i}\right)} r^{\left(h_{i}-h_{i-1}\right)^{2}}.
b. If F(T, \epsilon, r) is the Helmholtz free energy, show that the mean fraction of helical segments is
\theta(T)=-\frac{1}{N} \frac{\partial F}{\partial \epsilon}
while the mean number of junctions between melted and helical runs is
J(T)=-\frac{r}{k_{B} T} \frac{\partial F}{\partial r}.
c. By considering partial partition functions, ZNh and ZNm, for a molecule of N segments in which the last segment is in a helical or melted state, respectively, construct recursion relations from which the total partition function, ZN, can be found.
d. Find the eigenvalues of the corresponding 2 × 2 matrix and conclude that the free energy per segment of a very long DNA molecule is
f(T, \epsilon, r)=-k_{B} T \ln \frac{1}{2}\left[1+w+\sqrt{(1-w)^{2}+4 w r^{2}}\right]-\epsilon,
where w = qe−β\epsilon. Does this result take on the correct value at zero temperature?
e. In the limit that r vanishes show that the molecule undergoes a sharp melting transition at temperature
T_{m}=\frac{\epsilon}{k_{B} \ln q}.
Sketch the energy, entropy, and helical fraction θ(T) as a function of temperature and discuss the character of the transition.
f. If r is small but nonzero, sketch the behavior you expect for θ(T).
g. (Optional.) Show that when r is small but nonzero the sharp transition is “smeared out” over a temperature range of approximate width
\Delta T \approx \frac{4 \epsilon r}{k_{B} \ln ^{2} q}.
h. (Optional.) Show that the number of junctions J(T) defined in (b.) varies as Arα both at T = Tm and at low temperatures. Find the values of A and α in each case.
9.2 Thermodynamics of the one-dimensional Ising model
The Helmholtz free energy of the one-dimensional, nearest-neighbor Ising magnet is
F(T, H)=-N\left\{J+k_{B} T \ln \left[\cosh L+\sqrt{\sinh ^{2} L+e^{-4 K}}\right]\right\},
where
L=\frac{m H}{k_{B} T} \quad \text { and } \quad K=\frac{J}{k_{B} T}.
Use this result to show that
E(T, H=0)=-J N \tanh K,
C_{H}(T, H=0) \quad=\quad k_{B} N \frac{K^{2}}{\cosh ^{2} K},
M(T, H)=m N \frac{\sinh L}{\sqrt{\sinh ^{2} L+e^{-4 K}}},
\chi_{T}(T, H=0) \quad=\quad N \frac{m^{2}}{k_{B} T} e^{2 K}.
9.3 Zero-field one-dimensional Ising model
In class we found the free energy of a one-dimensional, nearest-neighbor Ising magnet with arbitrary magnetic field using the transfer matrix method. This problem finds the free energy in a much simpler way, which unfortunately works only in zero magnetic field.
a. Show that the partition function can be written as
Z_{N}=\sum_{s_{1}=\pm 1} \sum_{s_{2}=\pm 1} e^{K s_{1} s_{2}} \sum_{s_{3}=\pm 1} e^{K s_{2} s_{3}} \cdots \sum_{s_{N-1}=\pm 1} e^{K s_{N-2} s_{N-1}} \sum_{s_{N}=\pm 1} e^{K s_{N-1} s_{N}}.
b. Show that the last sum is
\sum_{s_{N}=\pm 1} e^{K s_{N-1} s_{N}}=2 \cosh K,
regardless of the value of sN−1.
c. Conclude that
Z_{N}=2^{N} \cosh ^{N-1} K
and that the zero-field Helmholtz free energy per site is
f(T)=-k_{B} T \ln \left(2 \cosh \frac{J}{k_{B} T}\right).
d. Find the zero-field heat capacity, and show that it gives the expected behavior at very low temperatures.
9.4 Magnetization near the critical point: mean field approximation
Analyze the Ising model in the mean field approximation to show that the zero-field magnetization near the critical temperature is
M(T)=\left\{\begin{array}{ll}{m N a\left(\frac{T_{c}-T}{T_{c}}\right)^{1 / 2}} & {\text { for } T<T_{c}} \\ {0} & {\text { for } T>T_{c}}\end{array}\right.
Be sure to specify the value of the numerical constant a. (Hint: \tanh x=x-\frac{1}{3} x^{3}+\frac{2}{15} x^{5}+\cdots.) (Remark: Experiment shows that the magnetization is not precisely of the character predicted by mean field theory: While it does approach zero like (Tc − T)β, the exponent β is not 1/2 — for two-dimensional systems β = 1/8, while for three-dimensional systems β ≈ 0.326.)
9.5 Correlation functions for paramagnets
In a paramagnet (see problem 2.9) the spins are uncorrelated, i.e. the correlation function is
G_{i}(T, H)=0 \quad \text { for } \quad i \neq 0.
Use this fact to verify the correlation sum rule
\chi_{T}(T, H)=N \frac{m^{2}}{k_{B} T} \sum_{i} G_{i},
derived in problem 8.11.
9.6 Lattice gas—Ising magnet
In class we showed that for a lattice gas
\Xi(T, \mu)=\sum_{n_{1}=0}^{1} \sum_{n_{2}=0}^{1} \cdots \sum_{n_{N}=0}^{1}\left(\frac{v_{0}}{\lambda^{3}(T)}\right)^{N} e^{\beta \mu \sum_{i} n_{i}+\beta \epsilon \sum_{\mathrm{nn}} n_{i} n_{j}},
whereas for an Ising magnet
Z(T, H)=\sum_{s_{1}=\pm 1} \sum_{s_{2}=\pm 1} \cdots \sum_{s_{\mathcal{N}}=\pm 1} e^{\beta m H} \sum_{i} s_{i}+\beta J \sum_{\mathrm{nn}} s_{i} s_{j}
and we concluded that the lattice gas and Ising magnet were more-or-less equivalent, with chemical potential and magnetic field playing sort of analogous roles. These conclusions are indeed correct, but this problem renders them precise.
a. Show that an up spin is associated with an occupied site, and a down spin with a vacant site, through
n_{i}=\frac{1}{2}\left(s_{i}+1\right).
b. Write out the sum for Ξ(T, µ) in terms of the variables si, and show that the correspondence
\epsilon=4 J
\mu=2 m H-k_{B} T \ln \left(v_{0} / \lambda^{3}(T)\right)-4 q J
(where q is the number of nearest neighbors for each site on the lattice) leads to
p(T, \mu) v_{0}=m H-\frac{3}{2} q J-f(T, H),
where p(T, µ) is the pressure of the gas and f(T, H) is the free energy per spin of the magnet.
c. Interpret equation (9.100) using the phrase “escaping tendency”. (Is this a sensible question?)
d. (Hard.) Take derivatives of equation (9.101) to show that
\rho(T, \mu) v_{0} =\frac{1}{2}[1+M(T, H) / m \mathcal{N}],
4 \rho^{2} \kappa_{T}(T, \mu) v_{0} =\chi(T, H) / m^{2} \mathcal{N},
S_{\mathrm{gas}}-k_{B} N\left[\ln \left(v_{0} / \lambda^{3}(T)\right)+\frac{3}{2}\right] =S_{\mathrm{mag}},
C_{V}-\frac{3}{2} k_{B} N =C_{M}.
9.7 Estimates concerning exhaustive enumeration
Consider an Ising model with 6.02 × 1023 sites. How many distinct configurations can this system take on? Estimate the mass of paper and ink required to write out a single character. What mass would be required to write out this number of configurations in decimal notation? Compare your estimate to the mass of the earth.
9.8 Fluctuations in Monte Carlo simulation
When the mean energy of a system is determined through Monte Carlo simulation, the result will necessarily have an uncertainty due to the statistical character of the simulation. (The same is true of any other measured quantity.) So if mean energy is plotted as a function of temperature, the data points will not fall on a sharp line but instead within a broad band. Using a fluctuation-susceptibility relation, show that the width of the band depends on its slope. Will steep bands be wide or narrow?
9.9 The folded array representation
Implement the folded array representation of a triangular lattice subject to skew-periodic boundary conditions. Clue: The piece of lattice under study will be a parallelogram.
9.10 Monte Carlo project
Perform a Monte Carlo simulation on the Ising model. The precise form and direction of the simulation is up to you: here are some suggestions that you are free to use, combine, extend, or ignore.
a. Draw movies showing the spin configuration of a two-dimensional Ising model as the simulation proceeds. Discuss the qualitative character of the model at high temperatures, low temperatures, and near the critical temperature (which is known, from Onsager’s exact solution, to be kBTc/J = −2/ ln(\sqrt{2} − 1)).
b. Simulate the one-dimensional Ising model and compare your results to the analytic solution obtained in class. Consider using the BKL algorithm5 at low temperatures.
c. Simulate the DNA denaturation model of problem 9.1, and compare your results to the analytic results of that problem. You will need to modify the Metropolis algorithm.
d. Simulate a two- or three-dimensional Ising ferromagnet at zero field, using an initial configuration of all spins up. Monitor the magnetization for a number of temperatures ranging from kBT ≈ 5J down to kBT = 0. Record both the equilibrium magnetization and the number of steps required to reach equilibrium, and plot these as a function of temperature. Can you locate the critical temperature?
e. Monitor both the mean energy (or magnetization) and the fluctuations in energy (or magnetization). Use a fluctuation-susceptibility relation to find the heat capacity (or susceptibility). In particular, show how a simulation at zero magnetic field can still give information about the magnetic susceptibility.
f. Verify the relation discussed in problem 9.8.
g. Implement the Wolff algorithm6 for improved simulation near the critical point.
h. Use finite size scaling7 to obtain accurate results near the critical point.
i. Compare the BKL and Wolff algorithms at low temperature.
j. Find the correlation function
G_{i}=\left\langle s_{0} s_{i}\right\rangle-\left\langle s_{0}\right\rangle^{2}
for a few values of T and H. How does it behave as the critical point is approached? k. (Very ambitious.) Verify the correlation-susceptibility relation (9.46).
5A.B. Bortz, J.L. Lebowitz, and M.H. Kalos, J. Comput. Phys., 17 (1975) 10–18.
6U. Wolff, Phys. Rev. Lett. 62 (1989) 361–364. J.-S. Wang and R.H. Swendsen, Physica A 167 (1990) 565–579.
7H. Gould and J. Tobochnik, An Introduction to Computer Simulation Methods: Applications to Physical Systems, part I (Addison-Wesley, Reading, Mass., 1988) sections 12.4 and 16.5


