7.1: Work
( \newcommand{\kernel}{\mathrm{null}\,}\)
Review Exercises
- Section A1.3 on the scalar product.
- Section A2.3 on integrals.
We introduce the concept of work as the starting point for building models using energy instead of forces. Work is a scalar quantity that is meant to represent how a force exerted on an object over a given distance results in a change in speed of that object. We will first introduce the concept of work done by a force on an object, and then look at how work can change the kinematics of the object. This is analogous to how we first defined the concept of force, and then looked at how force affects motion (by using Newton's Second Law, which connected the concept of force to the acceleration of the object).
The work done by a force, →F, on an object over a displacement, →d, is defined to be:
W=→F⋅→d=Fdcosθ=Fxdx+Fydy+Fzdz
where θ is the angle between the vectors when they are placed tail to tail, as in Figure 7.1.1. The dimension of work, force times displacement, is also called "energy''. The S.I. unit for energy is the Joule (abbreviated J) which is equivalent to Nm or kg m2/s2 in base units.
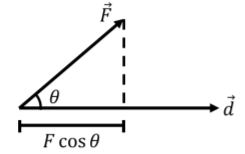
The work "done'' by the force is the scalar product of the force vector and the displacement vector of the object. We say that the force "does work'' if it is exerted while the object moves (has a displacement vector) and in such a way that the scalar product of the force and displacement vectors is non-zero. A force that is perpendicular to the displacement vector of an object does no work (since the scalar product of two perpendicular vectors is zero). A force exerted in the same direction as the displacement will do positive work (cosθ positive), and a force in the opposite direction of the displacement will do negative work (cosθ negative). As we will see, positive work corresponds to increasing the speed of the object, whereas negative work corresponds to decreasing its speed. No work corresponds to no change in speed (but could corresponds to a change in velocity).
A pendulum of length R consists of a mass connected to a string (Figure 7.1.2). The string exerts a force of tension →FT on the mass. What is the work done by tension when the pendulum swings through an angle θ?
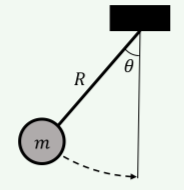
- W=FTRθ
- W=FTR(1−cosθ)
- Tension does no work on the mass.
- Answer
- 3.
You may be tempted to ask, "Why work? Why not something else? Why that scalar product in particular? How could we possibly have thought of that?''. In general, it seems arbitrary that we introduce the quantity "work'' and then find that it leads to a convenient way of building models. However, we did not just pull this quantity out of thin air! Many theorists, over many years, tried all sorts of quantities and ways to rephrase Newton's Theory that were not helpful. The quantities that make it into textbooks are the ones that turned out to be useful. You should also keep in mind that, just like force, work is a "made-up'' mathematical tool that is helpful in describing the world around us. There is no such thing as work or energy; they are just useful mathematical tools.
Work in one dimension.
Work involves vectors, so we can first examine the concept in one dimension, before extending this to two and three dimensions. We can choose x as the coordinate in one dimension, so that all vectors only have an x component. We can write a force vector as →F=Fˆx, where F is the x component of the force (which could be positive or negative). A displacement vector can be written as →d=dˆx, where again, d is the x component of the displacement, and can be positive or negative. In one dimension, work is thus:
W=→F⋅→d=(Fˆx)⋅(dˆx)=Fd(ˆx⋅ˆx)=Fd
where ˆx⋅ˆx=1. Consider, for example, the work done by a force, →F, on a box, as the box moves along the x axis from position x=x0 to position x=x1, as shown in Figure 7.1.3.
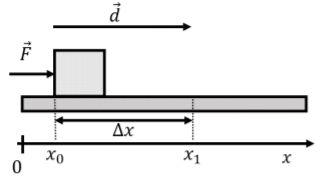
We can write the length of the displacement vector as ||→d||=d=Δx=x1−x0. The work done by the force is given by:
W=→F⋅→d=Fˆx⋅Δxˆx=FΔx=F(x1−x0)
which is a positive quantity, since x1>x0, with our choice of coordinate system.
A constant force in the positive x direction, →F, acts on a box, as in Figure 7.1.3. Consider the work done by →F as the box moves from x1 to x0. How does it compare to the work done by →F when moving from x0 to x1 (that we calculated above)?
- →F does no work on the box when it moves from x0 to x1.
- The work has the same magnitude as before, but the work is now negative.
- The work done by →F is the same in both cases.
- Answer
- B.
Work in one dimension - varying force
Suppose that instead of a constant force, →F, we have a force that changes with position, →F(x), and can take on three different values between x=x0 and x=x3:
→F(x)={F1ˆxx<ΔxF2ˆxΔx≤x<2ΔxF3ˆx2Δx≤x
as illustrated in Figure 7.1.3, which shows the force on an object as it moves from position x=x0 to position x=x3$, along three (equal) displacement vectors, →d1=→d2=→d3=Δxˆx
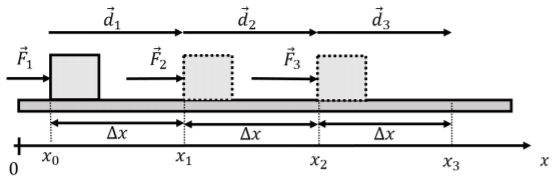
The total work done by the force over the three separate displacements is the sum of the work done over each displacement:
Wtot=W1+W2+W3=→F1⋅→d2+→F2⋅→d2+→F3⋅→d3=F1Δx+F2Δx+F3Δx
If instead of 3 segments we had N segments and the x component of the force had the N corresponding values Fi in the N segments, the total work done by the force would be:
Wtot=N∑i=0→Fi⋅Δ→x
where we introduced a vector Δ→x to be the vector of length Δx pointing in the positive x direction. In the limit where →F(x) changes continuously as a function of position, we take the limit of an infinite number of infinitely small segments of length dx, and the sum becomes an integral:
Wtot=∫xfx0→F(x)⋅d→x
where the work was calculated in going from x=x0 to x=xf, and d→x=dxˆx is an infinitely small displacement vector (of length dx) in the positive x direction.
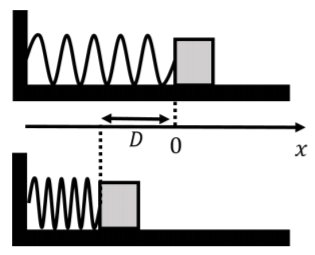
A block is pressed against the free end of a horizontal spring with spring constant, k, so as to compress the spring by a distance D relative to its rest length, as shown in Figure 7.1.5. The other end of the spring is fixed to a wall. What is the work done by the spring force on the block in going from x=−D to x=0? What is the work done by the block on the spring over the same displacement?
Solution
The force exerted by the spring on the block changes continuously with position, according to Hooke's law: →F(x)=−kxˆx
and points in the positive x direction when the end of the spring has a negative $x$ position (with our coordinate choice illustrated in Figure 7.1.5, where the origin is located at the rest length of the spring). To calculate the work done by the force, we sum the work done by the force over many infinitesimally small displacements d→x (using an integral):
W=∫0−D→F(x)⋅d→x=∫0−D(−kxˆx)⋅(dxˆx)=∫0−D−kxdx(ˆx⋅ˆx)=−∫0−Dkxdx=−[12kx2]0−D=12kD2
In order to determine the work that was done by the block on the spring, we need to determine the force, →F′(x), exerted by the block on the spring. By Newton's Third Law, this is equal in magnitude but opposite in direction to the force exerted by the spring on the block:
→F′(x)=−→F(x)=kxˆx
The work done by the block on the spring over the same displacement is:
W′=∫0−D→F′(x)⋅d→x=∫0−D(kxˆx)⋅(dxˆx)=∫0−Dkxdx=−12kD2
which is negative. This makes sense because the force exerted by the block on the spring is in the direction opposite to the direction of displacement, so the work should be negative.
Work in multiple dimensions
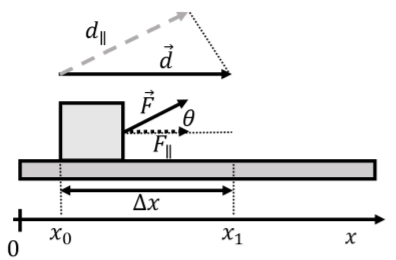
First, consider the work done by a force →F in pulling a crate over a displacement →d, in the case where the force is directed at an angle θ above the horizontal, as shown in Figure 7.1.6, and the displacement is along the x axis (or rather, we chose the x axis to be parallel to the displacement).
The work done by the force is given by:
W=→F⋅→d=Fdcosθ=F∥d=Fd∥
where we highlighted the fact that the scalar product "picks out'' components of vectors that are parallel to each other. F∥=Fcosθ is the component of →F that is parallel to →d, and d∥=dcosθ is the component of →d that is parallel to →F. These are also shown in Figure 7.1.6.
Brent and Dean pull two crates by using ropes that make the same angle above the horizontal and with the same force. The magnitude of the crates' displacement is the same, but Dean's crate moves horizontally on the ground while Brent's crate moves up a frictionless ramp that is parallel to the rope used to pull the crate. Who did more work on the crate?
- Dean because there is friction between his crate and the ground.
- Brent.
- They did the same amount of work.
- Answer
- B.
In general, if an object is moving along an arbitrary path, we cannot choose the $x$ axis to be parallel to the displacement or to the force. If the path can be sub-divided into straight segments over which the force is constant, as in Figure 7.1.7, we can calculate the work done by the force over each segment and add the work done in each segment together to obtain the total work done by the force. Note that, in general, the work done by a force as an object moves from one position to another depends on the particular path that was taken between the two positions, since different paths will have difference lengths.
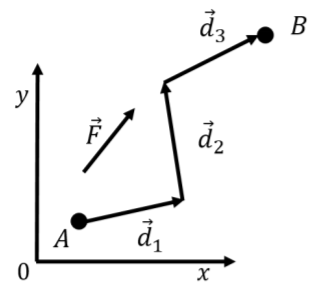
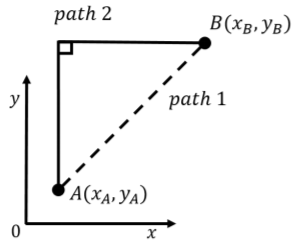
Compare the work done by the force of kinetic friction in sliding a crate along a horizontal surface from position A (coordinates xA,yA) to position B (coordinates xB,yB) using the two different paths depicted in Figure 7.1.8. Assume that the mass of the crate is m and that the coefficient of kinetic friction between the crate and the ground is μk.
Solution
The force of kinetic friction is always in the direction opposite to that of motion. Thus, regardless of the path taken, the force of friction will do negative work.
Let us first calculate the work done by the force of kinetic friction along the first path (the straight line). The force of kinetic friction will have a magnitude: fk=μkN=μkmg
The normal force will have the same magnitude as the weight because the crate is not moving (accelerating) in the direction perpendicular to the xy plane. The displacement vector from A to B can be written as: →d=(xB−xA)ˆx+(yB−yA)ˆy∴||→d||=d=√(xB−xA)2−(yB−yA)2
The force of kinetic friction will be in the opposite direction of the displacement vector, so the angle between the two vectors is 180∘(cosθ=−1). The work done by the force of kinetic friction is thus: W=→fk⋅→d=fkdcosθ=−μkmg√(xB−xA)2−(yB−yA)2 and is negative, as expected.
For path 2, we break up the motion into two segments, with displacements vectors →d1 (along y) and →d2 (along x). We can write the two displacement vectors as:
→d1=0ˆx+(yB−yA)ˆy∴||→d1||=d1=(yB−yA)→d2=(xB−xA)ˆx+0ˆy∴||→d2||=d2=(xB−xA)
Along each segment, the force of kinetic friction is anti-parallel to the displacement (note that the force of friction changes direction over the two segments), but the magnitude is fk=μkmg. The work done along the first segment is thus: W1=→fk⋅→d1=fkd1cosθ=−μkmg(yB−yA) The work done along the second segment is: W2=→fk⋅→d2=fkd2cosθ=−μkmg(xB−xA) And the total work done by the force of kinetic friction over the second path is: Wtot=W1+W2=−μkmg((xB−xA)+(yB−yA)) which is more work than was done along path 1. This makes sense because for both paths, the force of friction has the same magnitude and is always in the opposite direction of motion; thus, the longer the path, the more work will be done by the force.
A box of mass m is moved from the floor onto a table using two different paths, as shown in Figure 7.1.9. The table is a horizontal distance L away from where the box starts and a height H above the floor. Compare the work done by the weight of the box along the two possible paths.
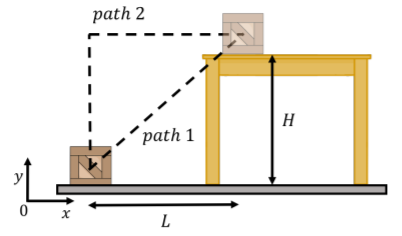
Solution
We can use a coordinate system such that the origin coincides with the initial position of the box. x is horizontal and y is vertical, as shown in Figure 7.1.9. The weight of the box can be written as:
→Fg=−mgˆy
and points in the negative y direction with a magnitude of mg. To calculate the work done by the weight along the first path, we first determine the corresponding displacement vector, →d:
→d=Lˆx+Hˆy
and we can then determine the work:
W=→Fg⋅→d=(−mgˆy)⋅(Lˆx+Hˆy)=Fxdx+Fydy=(0)(L)+(−mg)(H)=−mgH
Along path 1, the work done by the weight is negative, and does not depend on the horizontal distance L. Let us now calculate the work done along the second path, which we break up into two segments with displacement vectors →d1 (vertical) and →d2 (horizontal). The displacement vectors are:
→d1=Hˆy→d2=Lˆx
The work done along the vertical segment is:
W1=→Fg⋅→d1=(−mgˆy)⋅(Hˆy)=−mgH
The work done along the horizontal segment is:
W2=→Fg⋅→d2=(−mgˆy)⋅(Lˆx)=0
which is zero, because the force of gravity is always vertical and thus perpendicular to the displacement vector of the horizontal segment. The total work done by the weight along the second path is:
Wtot=W1+W2=−mgH
which is the same as the work done along path 1. As we will see, when a force is constant in magnitude and direction, the work that it does on an object in going from one position to another is independent of the path taken. This was not the case in Example 7.1.2, because the direction of the force of kinetic friction depends on the direction of the displacement.
Clare and Amelia go down two different slides, as shown in Figure 7.1.10. Clare and Amelia have the same mass and the slides have the same non-zero coefficients of friction.
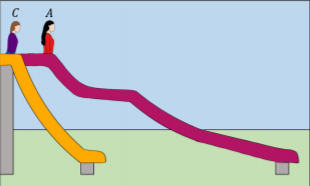
For each of the following forces, decide whether the force: does more work on Clare, does more work on Amelia, or does the same amount of work on both.
- The force of gravity...
- The force of friction...
- The normal force from the slide...
- Answer
-
Gravity does the same amount of work on both, friction does more work on Amelia, and the normal force does the same amount of work on both (the normal force does zero work, since it is always perpendicular to the displacement).
The most general case for which we can calculate the work done by a force is the case when the force changes continuously along a path where the displacement also changes direction continuously. This is illustrated in Figure 7.1.11 which shows an arbitrary path between two points A and B, and a force, →F(→r), that depends on position (→r). In general, the work done by the force on an object that goes from A to B will depend on the actual path that was taken.
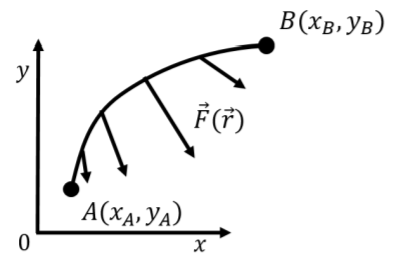
The strategy for calculating the work in the general case is the same: we break up the path into small straight segments with displacement vectors d→l (Figure 7.1.12) where we assume that the force is constant over the segment. The total work is the sum of the work over each segment:
W=∫BA→F(→r)⋅d→l
As usual, we use the integral symbol to indicate that you need to take an infinite number of infinitely small segments d→l in order to calculate the sum.
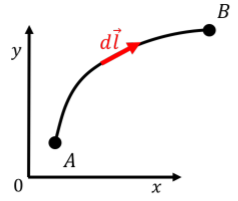
You should note that this is not an integral like any other that we have seen so far: the integral is not over a single integration variable (usually we use x), but it is the integral (the sum!) over the specific path that we have chosen in going from A to B. This is called a "path integral'', and is generally difficult to evaluate.
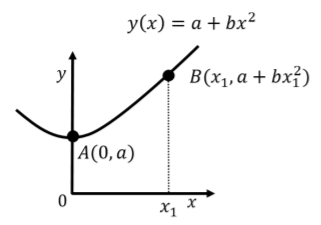
A force, →F(→r)=→F(x,y)=Fxˆx+Fyˆy, is exerted on an object. The object starts at position A and ends at position B, along a parabolic path, y(x)=a+bx2, as depicted in Figure 7.1.13. What is the work done by the force, →F, along this trajectory?
Solution
In this case, the force can change with position (if Fx and Fy are not constant), and the direction of the path changes continuously. When we break up the path into small segments d→l, we need to incorporate the equation of the parabola to include the fact that d→l$ must always be tangent to the parabola. Consider one small segment along the trajectory and the infinitesimal displacement vector d→l at that point, as in Figure 7.1.14.
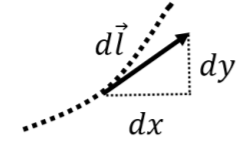
We can write the x and y components of the vector as infinitesimal distances, dx and dy, along the x and y axes, respectively. The vector d→l can thus be written:
d→l=dxˆx+dyˆy
The total work done by the force is then:
W=∫BA→F(→r)⋅d→l=∫BA(Fxˆx+Fyˆy)⋅(dxˆx+dyˆy)=∫BA(Fxdx+Fydy)∴W=∫BAFxdx+∫BAFydy
where in the last line, we simply used the property that the integral of a sum is the sum of the corresponding integrals. At this point, we have two integrals over integration variables (x and y) that are meaningful. However, we have not yet used the fact that our path is a parabola, and in general, we expect that the shape of the path is important. By saying that we are integrating (or calculating the work) over a specific path, we are really saying that x and y are not independent; that is, if we know the value of x at some point on the path, we know the corresponding value of y (y=a+bx2).
Since x and y are not independent, we can use a "substitution of variables'' in order to express y in terms of x, and dy in terms of dx$:
y(x)=a+bx2dydx=2bx∴dy=2bxdx
This allows us to convert the integral over y to an integral over x, which also allows us to be explicit for the limits of the integral (in our example, the integral goes from x=0 to x=x1):
W=∫BAFxdx+∫BAFydy=∫x10Fxdx+∫x10Fy(2bxdx)=∫x10(Fx+2bxFy)dx
where we would need to know how Fx and Fy depends on x and y in order to actually evaluate the integral.
For example, if the force were constant (Fx and Fy constant), then the work done along the parabolic path would be:
W=∫x10(Fx+2bxFy)dx=[Fxx+bFyx2]x10=Fxx0+bFyx20
As we mentioned earlier, if the force is constant in magnitude and direction, then the work done is independent of path. We can easily check this, using the displacement vector →d=x1ˆx+bx21ˆy:
W=→F⋅→d=(Fxˆx+Fyˆy)⋅(x1ˆx+bx21ˆy)=Fxx1+bFyx21
as we found above.
Net work done
So far, we have considered the work done on an object by a single force. If more than one force is exerted on an object, then each force can do work on the object, and we can calculate the "net work'' done on the object by adding together the work done by each force. We will show that this is equivalent to first calculating the net force on the object, Fnet (i.e. the vector sum of the forces on the object), and then calculating the work done by the net force.
Suppose that three forces, →F1, →F2, and →F3 are exerted on an object as it moves such that its displacement vector is →d. The net work done on the object is easily shown to be equivalent to the work done by the net force::
Wnet=W1+W2+W3=→F1⋅→d+→F2⋅→d+→F3⋅→d=(F1xdx+F1ydy+F1zdz)+(F2xdx+F2ydy+F2zdz)+(F3xdx+F3ydy+F3zdz)=(F1x+F2x+F3x)dx+(F1y+F2y+F3y)dy+(F1z+F2z+F3z)dz=→Fnet⋅→d
where →Fnet=→F1+→F2+→F3 is the net force. The result is easily generalized to any number of forces, including if those forces change as a function of position:
Wnet=∫BAFnet(→r)⋅d→l
You push with an unknown horizontal force, →F, against a crate of mass m that is located on an inclined plane that makes an angle $\theta$ with respect to the horizontal, as shown in Figure 7.1.15. The coefficient of kinetic friction between the crate and the incline is μk. You push in such a way that that crates moves at a constant speed up the incline. What is the net work done on the crate if it moves up the incline by a distance d?
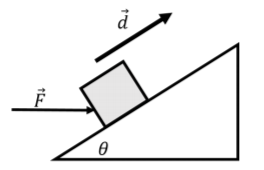
Solution
Although the answer may be obvious, let's go the long way about it and calculate the work done by each force, and then sum them together to get the total work done. We start by identifying the forces exerted on the crate:
- →F, the applied force, of unknown magnitude, →F.
- →Fg, the weight of the crate, with magnitude mg.
- →N, a normal force exerted by the incline.
- →fk, a force of kinetic friction, with magnitude μkN, that points in the direction opposite of →d.
These are shown in the free-body diagram in Figure 7.1.16, along with our choice of coordinate system, and the displacement vector.
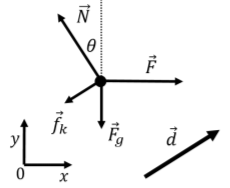
With our choice of coordinate system, the displacement vector is given by:
→d=d(cosθˆx+sinθˆy)
Before calculating the work done by each force, we need to determine the magnitude of the normal force (and thus of the force of kinetic friction). Since the crate is moving at a constant velocity, its acceleration is zero, so the sum of the forces must be zero. Writing out the y component of Newton's Second Law allows us to find the magnitude of the normal force:
∑Fy=Ncosθ−Fg−fksinθ=0∴mg=Ncosθ−μkNsinθ=N(cosθ−μksinθ)∴N=mgcosθ−μksinθ
Writing out the x component of Newton's Second Law allows us to find the magnitude of the unknown force F:
∑Fx=F−Nsinθ−fkcosθ=0∴F=Nsinθ+μkNcosθ=N(sinθ+μkcosθ)=mgsinθ+μkcosθcosθ−μksinθ
We now proceed to calculate the work done by each force. The work done by the normal force is identically zero, since it is perpendicular to the displacement vector. The work done by the applied force, →F=Fˆx, is:
WF=→F⋅→d=(Fˆx)⋅(d(cosθˆx+sinθˆy))=Fdcosθ=mgsinθ+μkcosθcosθ−μksinθdcosθ
The work done by the force of gravity, →Fg=−mgˆy, is:
Wg=→Fg⋅→d=(−mgˆy)⋅(d(cosθˆx+sinθˆy))=−mgdsinθ
The work done by the force of friction, →fk, noting that →fk and →d are antiparallel:
Wf=→fk⋅→d=−fkd=−μkNd=−μkmgcosθ−μksinθd
The net work done on the crate is thus:
Wnet=WF+Wg+Wf=mgsinθ+μkcosθcosθ−μksinθdcosθ−mgdsinθ−μkmgcosθ−μksinθd=mgd(sinθ+μkcosθcosθ−μksinθcosθ−sinθ−μk1cosθ−μksinθ)=mgd((sinθ+μkcosθ)cosθ−sinθ(cosθ−μksinθ)−μkcosθ−μksinθ)=mgd(sinθcosθ+μkcos2θ−sinθcosθ+μksin2θ−μkcosθ−μksinθ)=mgd(μk(cos2θ+sin2θ)−μkcosθ−μksinθ)=0
where we used the fact that cos2θ+sin2θ=1. Thus we find that the net work done on the crate is zero!
Discussion
Of course, this makes sense, because the net force on the crate is zero, since it is not accelerating, so the net work done is also zero. As a consequence, or rather, by construction, we have the condition that if the net work done on an object is zero, then that object does not accelerate. We thus have a scalar quantity (work) that can tell us something about whether an object is changing speed. In the next section, we introduce a new quantity, "kinetic energy'', to describe how an object's speed changes when the net work done is not zero. \end{example}
Pay close attention to the words "on'' and "by.'' There are a few things about this that can be tricky:
- In Example 7.1.5, we were asked to find the net work done on the crate. Sometimes, the question won't specify that it wants you to find the net work, and will just say "What is the work done on the crate?'' When you are just asked for the work done "on'' an object, the question is implicitly asking for the net work done on the object.
- Just because the net work done on an object is zero doesn't mean that the work done by each of the forces is zero. This may seem obvious, but it's easy to get tripped up on a test or exam. If you are reading a question about work and it says that the object is moving at a constant speed, it's tempting to just jump ahead and say that the work must be equal to zero. However, you can only say this if it's asking you for the net work done on the object. For instance, in Example 7.1.5, we concluded that since the crate was moving at a constant speed, the net work was equal to zero. But if the question asked you to find the work done on the crate by gravity, that would mean something different. The work done by gravity in this case is not equal to zero (it's actually negative).
- The work done "on'' an object is not the same as the net work done "by'' that object. For example, say you are in a tug-of-war and you pull the other team towards you, but you yourself do not move. The net work done on you is zero, but the work done by you is not zero. So, when you are talking about work, you should always state explicitly whether the work is being done "on'' the object or "by'' the object.
Note: The wording won't always be like this - sometimes it will say "How much work do you do on the box?'' instead of "How much work is done by you on the box,'' so always be careful. Still, looking for key words like "by'' and "on'' is a good place to start.
A 2kg box sits on a horizontal surface. A constant horizontal force of 6N is applied to the box. The box moves with a constant acceleration of 2m/s2. Which of the following has the greatest magnitude?
- The work done by the applied force.
- The work done by friction.
- The net work done on the box.
- Answer
- A.

