7.2: Kinetic energy and the work energy theorem
- Page ID
- 19407
At this point, you should be comfortable calculating the net work done on an object upon which several forces are exerted. As we saw in the previous section, the net work done on an object is connected to the object's acceleration; if the net force on the object is zero, then the net work done and acceleration are also zero. In this section, we derive a new quantity, kinetic energy, which allows us to connect the work done on an object with its change in speed. This will allow us to describe motion using only scalar quantities. Like the definition of work, the following derivation appears to "come out of thin air''. Remember, though, that theorists have tried all sorts of mathematical tricks to reformulate Newton's Theory, and this is the one that worked.
Consider the most general case of an object of mass \(m\) acted upon by a net force, \(\vec F^{net}(\vec r)\), which can vary in magnitude and direction. We wish to calculate the net work done on the object as it moves along an arbitrary path between two points, \(A\) and \(B\), in space, as shown in Figure \(\PageIndex{1}\). The instantaneous acceleration of the object, \(\vec a\), is shown along with an "element of the path'', \(d\vec l\).
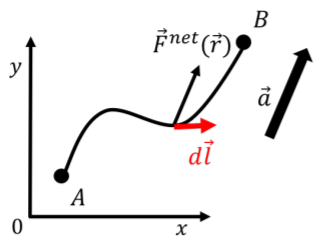
The net work done on the object can be written:
\begin{align*} W^{net} = \int_A^B F^{net}(\vec r) \cdot d\vec l \end{align*}
and is in general a difficult integral to evaluate for an arbitrary path. Our goal is to find a way to evaluate this integral by finding a function, \(K\), with the property that:
\begin{align*} \int_A^B F^{net}(\vec r) \cdot d\vec l =K_B - K_A \end{align*}
That is, we will only have to evaluate \(K\) at the end points of the path in order to determine the value of the integral. In this way, the function \(K\) is akin to an anti-derivative.
In order to determine the form for the function \(K\), we start by noting that, by using Newton's Second Law, we can write the integral for work in terms of the acceleration of the object:
\begin{align*} \sum \vec F &= \vec F^{net} = m\vec a\\[4pt] \therefore \int_A^B F^{net}(\vec r) \cdot d\vec l &= \int_A^B m\vec a\cdot d\vec l =m\int_A^B \vec a\cdot d\vec l \end{align*}
where we assumed that the mass of the object does not change along the path and can thus be factored out of the integral. Consider the scalar product of the acceleration, \(\vec a\), and the path element, \(d\vec l=dx\hat x +dy\hat y + dz\hat z\), written in terms of the velocity vector:
\begin{align*} \vec a & = \frac{d\vec v}{dt}\\[4pt] \therefore \vec a\cdot d\vec l &= \frac{d\vec v}{dt}\cdot d\vec l\\[4pt] &=\left(\frac{dv_x}{dt}\hat x+ \frac{dv_y}{dt}\hat y + \frac{dv_z}{dt}\hat z\right) \cdot (dx\hat x +dy\hat y + dz\hat z)\\[4pt] &=\frac{dv_x}{dt}dx+\frac{dv_y}{dt}dy+\frac{dv_z}{dt}dz \end{align*}
Any of the terms in the sum can be re-arranged so that the time derivative acts on the element of path (\(dx, dy\), or \(dz\)) instead of the velocity, for example:
\begin{align*} \frac{dv_x}{dt}dx = \frac{dx}{dt}dv_x \end{align*}
where we recognize that \(\frac{dx}{dt} = v_x\). We can thus write the scalar product between the acceleration vector and the path element as:
\begin{align*} \vec a\cdot d\vec l&= \frac{dv_x}{dt}dx+\frac{dv_y}{dt}dy+\frac{dv_z}{dt}dz\\[4pt] &=\frac{dx}{dt}dv_x + \frac{dy}{dt}dv_y+\frac{dz}{dt}dv_z\\[4pt] &=v_xdv_x + v_ydv_y + v_zdv_z \end{align*}
The integral for the net work done can be written as:
\begin{align*} W^{net} &= \int_A^B F^{net}(\vec r) \cdot d\vec l =m \int_A^B (v_xdv_x + v_ydv_y + v_zdv_z)\\[4pt] &=m\int_A^B v_xdv_x +m\int_A^B v_ydv_y + m\int_A^B v_zdv_z \end{align*}
which corresponds to the sum of three integrals over the three independent components of the velocity vector. The components of the velocity vector are functions that change over the path and have fixed values at either end of the path. Let the velocity vector of the object at point \(A\) be \(\vec v_A=(v_{Ax}, v_{Ay}, v_{Az})\) and the velocity vector at point \(B\) be \(\vec v_B=(v_{Bx}, v_{By}, v_{Bz})\). The integral over, say, the \(x\) component of velocity is then:
\begin{align*} m\int_A^B v_xdv_x &= m\int_{v_{Ax}}^{v_{Bx}} v_xdv_x= m\left[\frac{1}{2}v_x^2 \right]_{v_{Ax}}^{v_{Bx}}\\[4pt] &=\frac{1}{2}m(v_{Bx}^2-v_{Ax}^2) \end{align*}
We can thus write the net work integral as:
\begin{align*} W^{net} &=m\int_A^B v_xdv_x +m\int_A^B v_ydv_y + m\int_A^B v_zdv_z\\[4pt] &=\frac{1}{2}m(v_{Bx}^2-v_{Ax}^2) + \frac{1}{2}m(v_{By}^2-v_{Ay}^2) +\frac{1}{2}m(v_{Bz}^2-v_{Az}^2)\\[4pt] &=\frac{1}{2}m(v_{Bx}^2+v_{By}^2+v_{Bz}^2)-\frac{1}{2}m(v_{Ax}^2+v_{Ay}^2+v_{Az}^2)\\[4pt] &=\frac{1}{2}mv_B^2 - \frac{1}{2}mv_A^2 \end{align*}
where we recognized that the magnitude (squared) of the velocity is given by \(v_A^2 = v_{Ax}^2+v_{Ay}^2+v_{Az}^2\). We have thus arrived at our desired result; namely, we have found a function of speed, \(K(v)\), that when evaluated at the endpoints of the path allows us to calculate the net work done on the object over that path:
\[K(v)=\frac{1}{2}mv^{2}\]
That is, if you know the speed at the start of the path, \(v_A\), and the speed at the end of the path, \(v_B\), then the net work done on the object along the path between \(A\) and \(B\) is given by:
\[W^{net}=\Delta K=K(v_{B})-K(v_{a})\]
We call \(K(v)\) the "kinetic energy'' of the object. We can say that the net work done on an object in going from \(A\) to \(B\) is equal to its change in kinetic energy (final kinetic energy minus initial kinetic energy). It is important to note that we defined kinetic energy in a way that it is equal to the net work done. You may have already seen kinetic energy from past introductions to physics as a quantity that is just given; here, we instead derived a function that has the desired property of being equal to the net work done and called it "kinetic energy''.
The relation between the net work done and the change in kinetic energy is called the "Work-Energy Theorem'' (or Work-Energy Principle). It is the connection that we were looking for between the dynamics (the forces from which we calculate work) and the kinematics (the change in kinetic energy). Unlike Newton's Second Law, which relates two vector quantities (the vector sum of the forces and the acceleration vector), the Work-Energy Theorem relates two scalar quantities to each other (work and kinetic energy). Although we introduced the kinetic energy as a way to calculate the integral for the net work, if you know the value of the net work done on an object, then the Work-Energy Theorem can be used to calculate the change in speed of the object.
Most importantly, the Work-Energy theorem introduces the concept of "energy''. As we will see in later chapters, there are other forms of energy in addition to work and kinetic energy. The Work-Energy Theorem is the starting point for the idea that you can convert one form of energy into another. The Work-Energy Theorem tells us how a force, by doing work, can provide kinetic energy to an object or remove kinetic energy from an object.
A net work of \(W\) was done on an object of mass \(m\) that started at rest. What is the speed of the object after the work has been done on the object?
Solution
Using the Work-Energy Theorem:
\begin{align*} W = \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 \end{align*}
where \(v_i\) is the initial speed of the object and \(v_f\) is its final speed. Since the initial speed is zero, we can easily find the final speed:
\begin{align*} v_f = \sqrt{\frac{2W}{m}} \end{align*}
A block is pressed against the free end of a horizontal spring with spring constant, \(k\), so as to compress the spring by a distance \(D\) relative to its rest length, as shown in Figure \(\PageIndex{2}\). The other end of the spring is fixed to a wall.
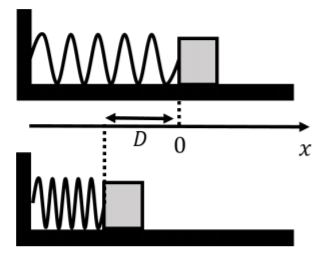
If the block is released from rest and there is no friction between the block and the horizontal surface, what is the speed of the block when it leaves the spring?
Solution
This is the same problem that we presented in Chapter 6 in Example 6.2.2, where we solved a differential equation to find the speed.
Our first step is to calculate the net work done on the object in going from \(x=-D\) to \(x=0\) (which corresponds to when the object leaves the spring, as discussed in Example 6.2.2). The forces on the object are:
- \(\vec F_g\), its weight, with magnitude \(mg\).
- \(\vec N\), the normal force exerted by the ground.
- \(\vec F(x)\), the force from the spring, with magnitude \(kx\).
Both the normal force and weight are perpendicular to the displacement, so they will do no work. The net work done is thus the work done by the spring, which we calculated in Example 7.1.1 to be:
\begin{align*} W^{net} = W_F = \frac{1}{2}kD^2 \end{align*}
By the Work-Energy Theorem, this is equal to the change in kinetic energy. Noting that the object started at rest (\(v_i=0\)), the final speed \(v_f\) is found to be:
\begin{align*} W^{net} &= \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 = \frac{1}{2}mv_f^2 - 0\\[4pt] \frac{1}{2}kD^2 &=\frac{1}{2}mv_f^2\\[4pt] \therefore v_f &=\sqrt{\frac{kD^2}{m}} \end{align*}
A block is pressed against the free end of a horizontal spring with spring constant, \(k\), so as to compress the spring by a distance \(D\) relative to its rest length, as shown in Figure \(\PageIndex{3}\). The other end of the spring is fixed to a wall.
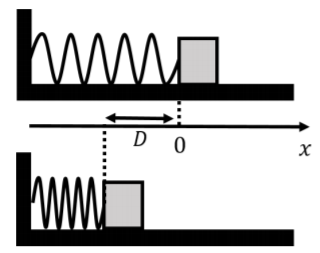
If the block is released from rest and the coefficient of kinetic friction between the block and the horizontal surface is \(\mu_k\), what is the speed of the block when it leaves the spring?
Solution
This is the same example as the previous one, but with kinetic friction. The forces on the block are:
- \(\vec F_g\), its weight, with magnitude \(mg\).
- \(\vec N\), the normal force exerted by the ground on the block.
- \(\vec F(x)\), the force from the spring, with magnitude \(kx\).
- \(\vec f_k\), the force of kinetic friction, with magnitude \(\mu_kN\).
Both the normal force and weight are perpendicular to the displacement, so they will do no work. Furthermore, since the acceleration in the vertical direction is zero, the normal force will have the same magnitude as the weight (\(N=mg\)). The magnitude of the force of kinetic friction is thus \(f_k = \mu_k mg\). The net work done will be the sum of the work done by the spring, \(W_F\), and the work done by friction, \(W_f\):
\begin{align*} W^{net} = W_F + W_f \end{align*}
We have already determined the work done by the spring:
\begin{align*} W_F = \frac{1}{2}kD^2 \end{align*}
The work done by the force of kinetic friction will be negative (since it is in the direction opposite of the motion) and is given by:
\begin{align*} W_f = \vec f_k \cdot \vec d = -f_kD = -\mu_kmgD \end{align*}
Applying the work energy theorem, and noting that the block started at rest (\(v_i=0\)), the final speed \(v_f\) is found to be:
\begin{align*} W^{net} =W_F + W_f&= \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2 \\[4pt] \frac{1}{2}kD^2-\mu_kmgD &=\frac{1}{2}mv_f^2\\[4pt] \therefore v_f &=\sqrt{\frac{kD^2}{m}-2\mu_kgD} \end{align*}
Discussion:
We can think of this in terms of the concept of energy. The spring does positive work on the block, and so it increases its kinetic energy. Friction does negative work on the block, decreasing its kinetic energy. Only the spring is "introducing'' energy into the block, as friction is removing that energy by doing negative work. Another way to think about it is that the spring is inputting energy; some of that energy goes into increasing the kinetic energy of the block, and some of it is lost by friction. The energy that is lost to friction can be thought of as "thermal energy'' (heat) that goes up into heating the block and the surface. Indeed, if you rub your hand against the table, you will notice that it gets warmer; you are losing some of the energy introduced to your hand by the work done by your arm into heating up the table and your hand! This shows that we can think about modeling friction using thermal energy rather than a force.