7.6: Sample Problems and Solutions

Exercise \(\PageIndex{1}\)

A ski jump can is modeled as a ramp of height \(h=5\text{m}\), as shown in Figure \(\PageIndex{1}\). The landing area is at the same height as the bottom of the ramp. A skier of mass \(m=80\text{kg}\) is moving at a speed \(v_i=15\text{m/s}\) when they reach the bottom of the ramp. When the skier lands the jump, their speed is measured to be \(v_f=12\text{m/s}\). Ignore air resistance.

Figure \(\PageIndex{1}\): A person of mass \(m\) goes off a ski jump of height \(h\).

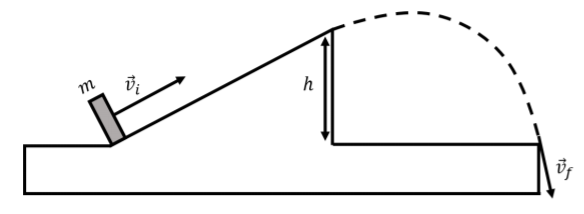
1. What is the speed of the skier the instant they leave the ski jump, at the top of the ramp?
2. Use the answer from part (a) to find the work done by friction the friction between the ramp and the skier.

Answer

We start by defining a coordinate system. We choose the \(x\) axis to be horizontal and positive in the direction of motion, and we choose the \(y\) axis to be vertical and the positive direction upwards.

We will determine the speed at the top of the ramp, \(v_t\), using the Work-Energy Theorem:

\begin{align*} W^{net}=\frac{1}{2}mv_f^2-\frac{1}{2}mv_t^2 \end{align*}

where \(W^{net}\) is the net work done on the skier as they "fly'' through the air. While the skier is in the air, the only force acting on them is gravity, \(\vec F=-mg\hat y\). The path of the skier is a parabola, so that the displacement vector changes direction continuously.

The work done by gravity is given by:

\begin{align*} W = \int \vec F_g \cdot d\vec l \end{align*}

where \(d\vec l\) is an infinitesimal displacement along the trajectory, as shown in Figure \(\PageIndex{2}\).

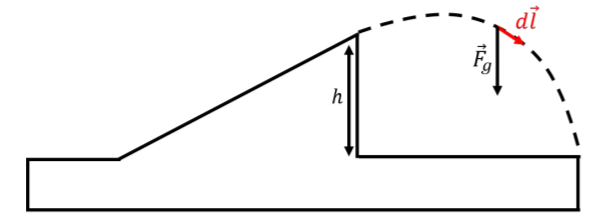
Figure \(\PageIndex{2}\): Infinitesimal displacement along the trajectory of the jump.

The displacement vector will have \(x\) and \(y\) components:

\begin{align*} d\vec l = dx \hat x + dy \hat y \end{align*}

The scalar product with the force of gravity is thus:

\begin{align*} \vec F_g \cdot d\vec l &= (-mg\hat y) \cdot (dx \hat x + dy \hat y)= -mgdy \end{align*}

The work done by gravity can thus be converted into an integral over \(y\) (for which we know the start and end values), and is given by:

\begin{align*} W = \int \vec F_g \cdot d\vec l = \int_h^0 -mgdy = [-mgy]_h^0 = mgh \end{align*}

The work done by gravity is positive, which makes sense, since the force of gravity is generally in the same direction as the net displacement (downwards). We did not need to take into account the specific shape of the trajectory, because the force was constant in magnitude and direction (see Example 7.1.4).

We can now find the speed of the skier when they leave the jump using the Work-Energy theorem:

\begin{align*} W^{net}&=\frac{1}{2}mv_f^2-\frac{1}{2}mv_t^2\\ mgh &= \frac{1}{2}mv_f^2-\frac{1}{2}mv_t^2\\ \therefore v_t&=\sqrt{v_f^2-2gh}=\sqrt{(12\text{m/s})^2 - 2(9.8\text{m/s}^{2})(5\text{m})}=6.8\text{m/s} \end{align*}

b. We can again use the Work-Energy Theorem to determine the work done by friction as the skier slides up the ramp. We know that the speed of the skier at the bottom of the ramp is \(v_i\), and we just found that the speed of the skier at the top of the ramp is \(v_t=\sqrt{v_f^2-2gh}\). The net work done on the skier going up the ramp is equal to:

\begin{align*} W^{net}&=\frac{1}{2}mv_t^2-\frac{1}{2}mv_i^2\\ &=\frac{1}{2}m(v_t^2-v_i^2) = \frac{1}{2}m(v_f^2-2gh -v_i^2)\\ &=\frac{1}{2}m(v_f^2-v_i^2)-mgh \end{align*}

The net work done is also the sum of the work done by each of the forces acting on the skier as they slide up the ramp. The forces on the skier are the force of gravity, the force of friction, and the normal force. The normal force does no work, since it is always perpendicular to the displacement. The net work is thus the sum of the work done by the force gravity, \(W_g\), and the work done by the force of friction, \(W_f\), over the displacement corresponding to the length of the ramp:

\begin{align*} W^{net}=W_g+W_f \end{align*}

The work done by gravity is:

\begin{align*} W_g = \vec F_g \cdot \vec d = (-mg\hat y) \cdot (d_x\hat x + h \hat y) = -mgh \end{align*}

where \(\vec d\) is the displacement vector up the ramp (unknown horizontal distance, \(d_x\), and vertical distance, \(h\)). We can now determine the work done by the force of friction:

\begin{align*} W^{net}&=W_g+W_f\\ \frac{1}{2}m(v_f^2-v_i^2)-mgh &= -mgh + W_f\\ \therefore W_f &= \frac{1}{2}m(v_f^2-v_i^2) = \frac{1}{2}(80\text{kg})((12\text{m/s})^2-(15\text{m/s})^2)=-3240\text{J} \end{align*}

And we find that the force of friction did negative work (it reduced the kinetic energy of the skier).

Discussion:

Over the course of the jump, the skier started at the bottom of the ramp with a given kinetic energy, then lost some of that energy going up the ramp (in the form of loss to friction and negative work done by gravity). During the airborne phase, gravity did positive work and the skier gained back some of the kinetic energy that they had lost going up the ramp. Thus the net work done by the force of friction is the difference in kinetic energies between the final landing point and the beginning of the ramp, because friction is the only force that did a net amount of (negative) work over the whole trajectory (gravity did no net work over the whole trajectory). This example shows how we can start to think about energy as something that is "conserved'', which we will explore in more detail in the next chapter.

Exercise \(\PageIndex{2}\)

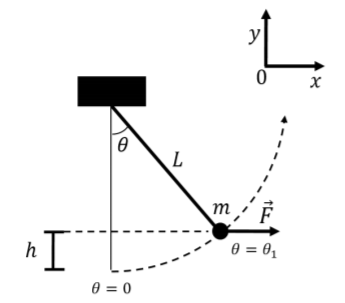
A child of mass \(m\) sits on a swing of length \(L\), as in Figure \(\PageIndex{3}\). You push the child with a horizontal force \(\vec F\). You apply the force in such a way that the child moves at a constant speed (note that \(\vec F\) will not have a constant magnitude).}

1. How much work do you do to move the child from \(\theta=0\) to \(\theta=\theta_1\)?
2. Use a detailed diagram to show that the work done by \(\vec F\) is equal to \(mgh\), where \(h\) is the change in height of the child.

Figure \(\PageIndex{3}\): A child on a swing is pushed from \(θ = 0\) to \(θ = θ_{1}\) at constant speed with a horizontal force, \(\vec F\).

Answer

a. We want to find the work done by the applied force \(\vec F\). We first need to find an expression for the magnitude of \(\vec F\), based on the fact that the child is not accelerating. The forces on the child are:

• \(\vec F_g\), their weight, with magnitude \(mg\).
• \(\vec F_T\), the tension in the rope, which changes with the angle, \(\theta\).
• \(\vec F\), the applied force, which change in magnitude as the angle, \(\theta\), changes.

The forces are illustrated in Figure \(\PageIndex{4}\).

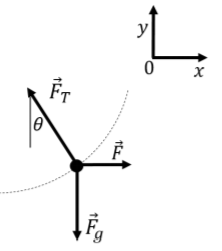
Figure \(\PageIndex{4}\): A free-body diagram of the forces exerted on the child.

The child is moving at a constant speed, so the net force is equal to zero. The sum of the \(x\) and \(y\) components of the forces are equal to zero (Newton's Second Law):

\begin{align*} \sum F_x &= F-F_T\sin\theta =0\\ \sum F_y &= F_T\cos\theta -mg = 0 \end{align*}

Rearranging these equations gives:

\begin{align*} F&=F_T\sin\theta\\ mg&=F_T\cos\theta \end{align*}

We want an expression for \(F\) that does not depend on \(F_T\) (since \(F_T\) is unknown), so we can divide one equation by the other:

\begin{align*} \frac{F}{mg} &= \frac{F_T\sin\theta}{F_T\cos\theta}=\tan\theta\\ \therefore F(\theta)&=mg\tan\theta \end{align*}

where we indicated that the force \(\vec F(\theta)\) depends on the angle \(\theta\). The work done by the force, \(\vec F\), is given by:

\begin{align*} W_F=\int_A^B\vec F(\theta) \cdot d\vec l \end{align*}

\(d\vec l\) is the "path element'' along part of the arc of circle over which the child moves, as illustrated in Figure \(\PageIndex{5}\). We have an expression for how \(\vec F\) changes in magnitude as a function of the angle \(\theta\), and it would thus be convenient to perform the integral over the angle \(\theta\).

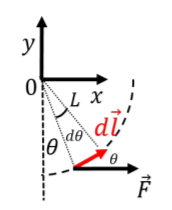
Figure \(\PageIndex{5}\): A path element along the circular trajectory of the swing.

We can use polar coordinate, \((r,\theta)\), instead of Cartesian coordinates to describe the displacement vector, \(d\vec l\). If the vector subtends an arc on the circle that makes an infinitesimal angle, \(d\theta\), as illustrated, then the length of the vector \(d\vec l\) is given by:

\begin{align*} dl = L d\theta \end{align*}

where \(L\) is the radius of the circle. The vector \(d\vec l\) makes an angle \(\theta\) with the horizontal, and thus with the vector, \(\vec F\). The dot product between \(\vec F\) and \(d\vec l\) can thus be written as:

\begin{align*} \vec F(\theta) \cdot d\vec l = Fdl\cos\theta=(mg\tan\theta)(Ld\theta)\cos\theta=mgL\sin\theta d\theta \end{align*}

We can now write the integral for the work using limit that are based on the angle \(\theta\), from \(\theta=0\) to \(\theta=\theta_1\):

\begin{align*} W&=\int_0^{\theta_1}mgL\sin\theta d\theta\\ &=mgL[-\cos\theta]_0^{\theta_1}=mgL(1-\cos\theta_1) \end{align*}

b. We know that the work done by \(\vec F\) is \(W=mgL(1-\cos\theta_1)\). So, we want to prove that \(L(1-\cos\theta_1)\) is equal to \(h\). Expanding \(L(1-\cos\theta_1)\) gives:

\begin{align*} L(1-\cos\theta_1)&=L-L\cos\theta_1 \end{align*}

This can be illustrated on a diagram, as in Figure \(\PageIndex{6}\), which shows that \(h\) is equal to \(L-L\cos\theta\).

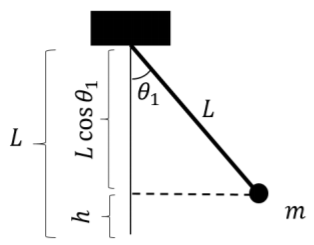
Figure \(\PageIndex{6}\): A diagram showing the geometry of the problem.

Discussion:

The net force acting on the mass is equal to zero, so the net work must be equal to zero. The two forces that do work on the mass are the applied force \(\vec F\), and gravity. The work done by the applied force if \(mgh\), so the work done by gravity must be \(-mgh\).