8: Potential Energy and Conservation of Energy
- Page ID
- 19411
In this chapter, we continue to develop the concept of energy in order to introduce a different formulation for Classical Physics that does not use forces. Although we can describe many phenomena using energy instead of forces, this method is completely equivalent to using Newton’s Three Laws. As such, this method can be derived from Newton’s formulation, as we will see. Because energy is a scalar quantity, for many problems, it leads to models that are much easier to develop mathematically than if one had used forces. The chapter will conclude with a presentation of the more modern approach, using “Lagrangian Mechanics”, that is currently preferred in physics and forms the basis for extending our description of physics to the microscopic world (e.g. quantum mechanics).
Learning Objectives
- Understand the difference between conservative and non-conservative forces.
- Understand how to define potential energy for a conservative force.
- Understand how to use potential energy to calculate work.
- Understand the definition of mechanical energy.
- Understand how to use conservation of mechanical energy.
- Understand how to apply the Lagrangian formulation in a simple case.
prelude
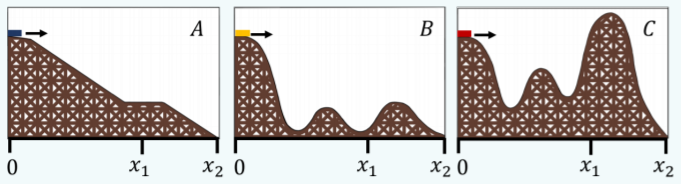
Three roller coaster carts start at position \(x = 0\), where they are all at the same height (Figure 8.1). All of the carts start with the same velocity. At \(x_{1}\), which roller coaster cart will be moving the fastest?
All of the roller coasters end at ground level, at \(x_{2}\). Which roller coaster cart will be moving the fastest at \(x_{2}\)? Will all of them make it to \(x_{2}\)? Who will get there first? Assume that the roller coaster track is frictionless.
Thumbnail: Roller coaster "Blue Fire" at Europa Park. (CC SA 3.0; Coaster J).