8.2: Potential Energy
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we introduce the concept of “potential energy”. Potential energy is a scalar function of position that can be defined for any conservative force in a way to make it easy to calculate the work done by that force over any path. Since the work done by a conservative force in going from position A to position B does not depend on the particular path taken, but only on the end points, we can write the work done by a conservative force in terms of a “potential energy function”, U(→r), that can be evaluated at the end points:
−W=−∫BA→F(→r)⋅d→l=U(→rB)−U(→rA)=ΔU
where we have have chosen to define the function U(→r) so that it relates to the negative of the work done for reasons that will be apparent in the next section. Figure 8.2.1 shows an example of an arbitrary path between two points A and B in two dimensions for which one could calculate the work done by a conservative force using a potential energy function.
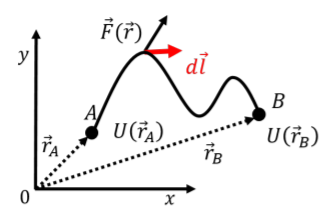
Once we know the function for the potential energy, U(→r), we can calculate the work done by the associated force along any path. In order to determine the function, U(→r), we can calculate the work that is done along a path over which the integral for work is easy (usually, a straight line).
For example, near the surface of the Earth, the force of gravity on an object of mass, m, is given by:
→Fg=−mgˆz
where we have defined the z axis to be vertical and positive upwards. We already showed in Example 8.1.1 that this force is conservative and that we can thus define a potential energy function. To do so, we can calculate the work done by the force of gravity over a straight vertical path, from position A to position B, as shown in Figure 8.2.2.
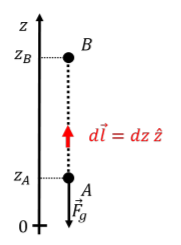
The work done by gravity from position A to position B is:
W=∫BA→F(→r)⋅d→l=∫zBzA(−mgˆz)⋅(dzˆz)=−mg∫zBzAdz=−mg(zB−zA)
By inspection, we can now identify the functional form for the potential energy function, U(→r).
We require that:
−W=U(→rB)−U(→rA)=U(zB)−U(zA)
where we replaced the position vector, →r, with the z coordinate, since this is a one dimensional situation. Therefore:
−W=mg(zB−zA)=U(zB)−U(zA)∴U(z)=mgz+C
and we have found that, for the force of gravity near the surface of the Earth, one can define a potential energy function (by inspection), U(z)=mgz+C.
It is important to note that, since it is only the difference in potential energy that matters when calculating the work done, the potential energy function can have an arbitrary constant, C, added to it. Thus, the value of the potential energy function is meaningless, and only differences in potential energy are meaningful and related to the work done on an object. In other words, it does not matter where the potential energy is equal to zero, and by choosing C, we can therefore choose a convenient location where the potential energy is zero.
When we found the work done by gravity, we defined positive z to be upwards. If we instead chose positive z to be downwards, how would the potential energy function be defined?
- The potential energy function would be the same, U(z)=mgz+C.
- The potential energy function would be the same but negative, U(z)=−mgz+C
- Answer
- B.
Can an object have a negative potential energy?
- Yes
- No
- Answer
- A. the constant C is specified by the situation and is arbitrary.
Calculate the work done by the force of gravity when a box of mass, m, is moved from the ground up onto a table that is a distance L away horizontally and H vertically, as illustrated in Figure 8.2.3. How much work must be done by a person moving the box?
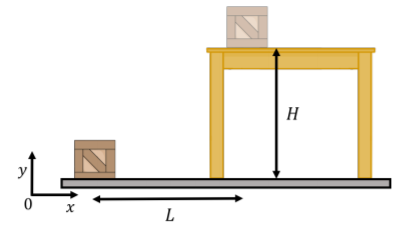
Solution
Since the force of gravity is conservative, we can use the potential energy function given by:
U(z)=mgz+C
to calculate the work done by the force of gravity when the box is moved. The work done by gravity will only depend on the change in height, H, as the potential energy function only depends on the z coordinate of an object. We can choose the origin of our coordinate system to be the ground and choose the constant C=0, so that the potential energy function at the starting position of the box is:
U(zA=0)=mg(0)=0
The potential energy function when the box is on the table, with z=H, is given by:
U(zB=H)=mgH
The change in potential energy, ΔU=U(zB)−U(zA) is equal to the negative of the work done by gravity. The work done by gravity, Wg, is thus:
−Wg=U(zB)−U(zA)=mgH−0∴Wg=−mgH
which is the same as what we found in Example 7.1.3 of Chapter 7. The work done by gravity is negative, as we found previously. This makes sense because gravity has a component opposite to the direction of motion.
The work done by a person, Wp, to move the box can easily be found by considering the net work done on the box. While the box is moving, only the person and gravity are exerting forces on the box, so those are the only two forces performing work. Since the box starts and ends at rest, the net work done on the box must be zero (no change in kinetic energy, recall the Work-Energy Theorem):
Wnet=0=Wg+Wp∴Wp=−Wg=mgH
Discussion
We find that the person had to do positive work, which makes sense, since they had to exert a force with a component in the direction of motion (upwards). It is also interesting to note that it does not matter if the person exerted a constant force or whether they varied the force that they exerted on the box as they moved it: the amount of work done by the person is fixed to be the negative of the work done by gravity.
The force exerted by a spring that is extended or compressed by a distance, x, is given by Hookes’ Law:
→F(x)=−kxˆx
where the x axis is defined to be co-linear with the spring and the origin is located at the rest position of the spring. Show that the force exerted by the spring onto an object is conservative and determine the corresponding potential energy function.
Solution
Since the force depends on position, it could be conservative, which we can check with the conditions from Equations 8.1.3, 8.1.4, 8.1.5:
∂Fz∂y−∂Fy∂z=0−0=0∂Fx∂z−∂Fz∂x=∂∂z(−kx))−0=0∂Fy∂x−∂Fx∂y=0−∂∂y(−kx))=0
and the force is indeed conservative. To determine the potential energy function, let us calculate the work done by the spring from position xA to position xB:
W=∫BA→F(→r)⋅d→l=∫xBxA(−kxˆx)⋅dxˆx=∫xBxA(−kx)dx=[−12kx2]xBxA=−(12kx2B−12kx2A)
Again, comparing with:
−W=U(→rB)−U(→rA)=U(xB)−U(xA)
We can identify the potential energy for a spring:
U(x)=12kx2+C
where, in general, the constant C can take any value. If we choose C=0, then the potential energy is zero when the spring is at rest, although it is not important what choice is made. Note that in one dimension, the potential energy function is the negative of the anti-derivative of the function that gives the x component of the force.
A conservative force acts on an object that is initially at rest. No other forces act on the object. Does the object move in a way that increases its potential energy or decreases its potential energy?
- Increases.
- Decreases.
- It depends on the choice of C for the corresponding potential energy.
- Answer
- B.
Recovering the force from potential energy
Given a (scalar) potential energy function, U(→r), it is possible to determine the (vector) force that is associated with it. Take, for example, the potential energy from a spring (Example 8.2.2):
U(x)=12kx2+C
As you recall from Example 8.2.2, to find this function (in one dimension), we took the x component of the spring force and (effectively) found the negative of its anti-derivative, which we defined as the potential energy function:
F(x)=−kxU(x)=−∫F(x)dx=∫(kx)dx=12kx2+C∴F(x)=−ddxU(x)
Thus, the force can be obtained from the negative of the potential energy function, by taking its derivative with respect to position.
In three dimensions, the situation is similar, although the potential energy function (and the components of the force vector) will generally depend on all three position coordinates, x, y, and z. In three dimensions, the the three components of the force vector are given by taking the gradient of the negative of the potential energy function1:
→F(→r)=−→∇U(→r)=−→∇U(x,y,z)
∴Fx(x,y,z)=−∂∂xU(x,y,z)
∴Fy(x,y,z)=−∂∂yU(x,y,z)
∴Fz(x,y,z)=−∂∂zU(x,y,z)
Footnotes
1. As you may recall from Appendix B, the gradient is a vector that points towards the direction of maximal increase in a multi-variate function.

