9.7: Sample problems and solutions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Geosynchronous satellites are satellites that are placed in a circular orbit around the Earth in such a way that their orbital period is synchronized with the 24 h rotation period of the Earth. The advantage of geosynchronous satellites is that they are always above the same point on Earth, which makes them useful for establishing communication networks. At what altitude must geosynchronous satellites be placed?
- Answer
-
When a satellite orbits the Earth, the only force on the satellite is the force of gravity from the Earth. Since the satellite is in a circular orbit, that force of gravity must point towards the center of the Earth in such a way that the satellite has the correct radial acceleration, aR, to stay in uniform circular motion:
ar=v2R
where v is the speed of the satellite, and R is the distance between the satellite and the center of the Earth (i.e. the center of the circular orbit). The magnitude of the force of gravity on the satellite of mass m is given by:
F=GMmR2
where M is the mass of the Earth. Newton’s Second Law applied to the satellite is:
∑Fr=F=mar∴GMmR2=mv2R
The speed of the satellite can be found from the fact that it must travel a distance of 2πR (the circumference of the orbit) in a period T = 24\text{ h}:
v=\frac{2\pi R}{T}
which we can substitute into the equation from Newton’s Second Law to find the distance R (i.e. the radius of the circular orbit):
\begin{aligned} G\frac{Mm}{R^{2}}&=m\frac{v^{2}}{R} \\[4pt] G\frac{M}{R^{2}}&=\frac{(2\pi R)^{2}}{T^{2}R} \\[4pt] G\frac{M}{R^{2}}&=\frac{4\pi ^{2}R}{T^{2}} \\[4pt] \therefore R&=\sqrt[3]{G\frac{MT^{2}}{4\pi ^{2}}} \\[4pt] &=\sqrt[3]{(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2}) \frac{(5.97\times 10^{24}\text{kg})(86400\text{s})^{2}}{4\pi ^{2}}} \\[4pt] &=42.2\times 10^{6}\text{m} \end{aligned}
which corresponds to the distance between the satellite and the center of the Earth. To obtain the “altitude”, h, namely the distance from the surface of the Earth to the satellite, we must subtract the radius of the Earth, R_{⊕} = 6.371 × 10^{6}\text{ m} from this distance:
h = R − R_{⊕} = 35.9 × 10^{6}\text{ m}
Thus, geosynchronous satellites are located at an altitude of approximately 36000\text{ km}.
Discussion
Note that we could have also easily used Kepler’s Third Law to determine the radius of the orbit, since we already know the period (24\text{ h}), and we know the value of the constant for Kepler’s Third Law from Example 9.2.2.
How much energy must be expended in order to place a satellite of mass m = 1000\text{ kg} in a geosynchronous circular orbit around the Earth, if the satellite is launched from the North Pole of the Earth? How much energy is this per kilogram of satellite placed in orbit?
- Answer
-
We need to calculate how much work must be done for the satellite to go from being at rest at the surface of the Earth to being in a geosynchronous orbit. That work will be done by a non-conservative force (a rocket engine). The work done by the non-conservative force, W, is equal to the satellite’s change in mechanical energy:
W = ∆E = E_{B} − E_{A}
The initial mechanical energy of the satellite, E_{A}, is given by its gravitational potential energy (it has no kinetic energy at the surface of the Earth when at the North Pole - on the equator, it would have kinetic energy due to the Earth’s rotation):
E_{A}=K+U=0-G\frac{Mm}{R_{⊕}}
where M = 5.97 × 10^{24}\text{ kg} is the mass of the Earth, and R_{⊕} = 6.731 × 10^{6}\text{ m} is the radius of the Earth.
In orbit, the energy of the rocket, E_{B}, is given by:
E_{B}=K+U=\frac{1}{2}mv^{2}-G\frac{Mm}{R}
where R = 42.2 × 10^{6}\text{ m} is the radius of the geosynchronous orbit (Problem 9.2.1) and v is the speed of the satellite in orbit. The speed is given by:
v=\frac{2\pi R}{T}
where T = 24\text{ h} is the orbital period. The net work that must be done to place the satellite in orbit is thus given by:
\begin{aligned} W&=E_{B}-E_{A}=\frac{1}{2}mv^{2}-G\frac{Mm}{R}-\left(-G\frac{Mm}{R_{⊕}} \right) \\[4pt] &=\frac{1}{2}m\frac{4\pi ^{2}R^{2}}{T^{2}}+GMm\left(\frac{1}{R_{⊕}}-\frac{1}{R} \right) \\[4pt] &=\frac{1}{2}(1000\text{kg})\frac{4\pi ^{2}(42.2\times 10^{6}\text{m})^{2}}{(86400\text{s})^{2}} \\[4pt] &+(6.67\times 10^{-11}\text{Nm}^{2}/\text{kg}^{2})(5.97\times 10^{24}\text{kg})(1000\text{kg})\left(\frac{1}{(6.731\times 10^{6}\text{m})}-\frac{1}{(42.2\times 10^{6}\text{m})} \right) \\[4pt] &=5.78\times 10^{10}\text{kg} \end{aligned}
This corresponds to the energy that must be imparted to a 1000 kg satellite for it to end up in a geosynchronous orbit. This corresponds to 5.78 × 10^{7}\text{ J/kg} as the energy required per kilogram of payload placed in geosynchronous orbit. Although we calculated work as if it were work done by a force, we can think of this work coming from stored chemical potential energy in the fuel of the rocket carrying the satellite.
Discussion
The energy that we found above is the minimum energy that one must provide to the satellite. In practice, in order to place a satellite in orbit, one will also need to provide enough energy to accelerate the rocket that carries the satellite up into orbit, which is typically much heavier than the satellite. If the satellite were instead launched from the equator of the Earth, the satellite would already have some initial kinetic energy due to the rotation of the Earth, and one would need to provide less energy to place it in orbit. This is the reason that most rockets are launched from near the equator (think French Guyana, Florida, Kazakhstan) in a direction that is roughly parallel with the Earth’s rotation.
Find an expression for the gravitational field due to a thin uniform rod of mass M at point P, which is a distance h above the midsection of the rod (Figure \PageIndex{1}).
- Answer
-
We cannot use Gauss’s law to determine the magnitude of the field because the gravitational field lacks symmetry (i.e. the field will be different at the ends of the rod than along the length of the rod). The gravitational field due to a body of mass M is given by:
\vec g(\vec r)=-\frac{GM}{r^{2}}\hat r
Our strategy will be to break the rod into very small segments of length dx. Each segment, of mass dM, will make a small contribution, d\vec g, to the gravitational field, as shown in Figure \PageIndex{2}. We will then take the sum of all these contributions to find the net field.
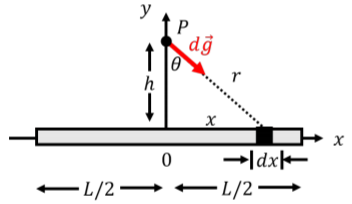
Figure \PageIndex{2}: A thin rod of mass M and length L produces a gravitational field at a point P located above the midsection of the rod. Each segment of the rod dx will contribute to the gravitational field. The gravitational field due to each segment is given by:
d\vec g=-\frac{GdM}{r^{2}}\hat r
The element of the field, d\vec g, will point in a different direction for each segment dx. You can conclude from Figure \PageIndex{2} that, due to symmetry, the x components of the field from each segment will cancel out (for the segment dx shown in the diagram, there will be an identical segment on the other side of the rod). The net field will point in the −\hat y direction, so we are only interested in the vertical component of d\vec g. Using our diagram, this means that we want to find the magnitude of dg\ cos θ:
dg\cos\theta = \frac{GdM}{r^{2}}\cos\theta
The magnitude of the gravitational field at point P is thus given by:
g=\int dg\cos\theta = \int \frac{GdM}{r^{2}}\cos\theta
The integral is written over dM, where both r, and θ are different for each different mass element, dM. We need to express any variable that changes for different mass elements in terms of a single variable of integration. We will choose θ as the variable of integration, and thus need to express r and dM in terms of θ, dθ, and other constants.
The distance, r, between P and a mass element dM located at angle θ is easily found to be:
\begin{aligned} r&=\frac{h}{\cos\theta} \\[4pt] \therefore\frac{1}{r^{2}}&=\frac{\cos^{2}\theta}{h^{2}} \end{aligned}
dM can easily be expressed in term of dx (the length of the mass element in the x direction) and λ, the mass per unit length of the rod:
dM = λdx = \frac{M}{L}dx
We now need to express dx in terms of dθ. This can be found as follows, by first expressing x in terms of θ, and then taking the derivative of x with respect to θ
\begin{aligned} x&=h\tan\theta \\[4pt] \therefore \frac{dx}{d\theta} &=\frac{h}{\cos^{2}\theta} \\[4pt] \therefore dx&=\frac{h}{\cos^{2}\theta}d\theta \end{aligned}
Now that we have found the small change in x that results from a small change in θ, we can write the mass element, dM, in terms of the dθ:
dM=\frac{M}{L}dx=\frac{M}{L}\frac{h}{\cos^{2}\theta}d\theta
We can now write the integral in terms of θ:
\begin{aligned} g=\int\frac{GdM}{r^{2}}\cos\theta &=G\int\frac{1}{r^{2}}\cos\theta dM \\[4pt] &=G\int \left(\frac{\cos^{2}\theta}{h^{2}} \right)\cos\theta\left( \frac{M}{L}\frac{h}{\cos^{2}\theta} \right) \\[4pt] &=\frac{GM}{Lh}\int\cos\theta d\theta \end{aligned}
Now that we have the integral over θ, we need to set the limits to correspond to the values of θ at each end of the rod. The angle will have the same magnitude for each end of the rod, θ_{0}, given by:
\sin\theta _{0}=\frac{L}{2\sqrt{h^{2}+\frac{L^{2}}{4}}}
The magnitude of the field is thus given by:
\begin{aligned} g&=\frac{GM}{Lh}\int _{-\theta _{0}}^{\theta _{0}}\cos\theta d\theta = \frac{GM}{Lh}[\sin\theta]_{-\theta _{0}}^{\theta _{0}} \\[4pt] &=\frac{2GM}{Lh}\sin\theta _{0}=\frac{2GM}{Lh}\frac{L}{2\sqrt{h^{2}+\frac{L^{2}}{4}}} \end{aligned}
The gravitational field at point P is thus given by:
\vec g=-\frac{2GM}{Lh}\frac{L}{2\sqrt{h^{2}+\frac{L^{2}}{4}}}\hat y

