10.1: Momentum
- Page ID
- 19429
Momentum of a point particle
We can define the momentum, \(\vec p\), of a particle of mass \(m\) and velocity \(\vec v\) as the vector quantity:
\[\vec p = m\vec v\]
Since this is a vector equation, it corresponds to three equations, one for each component of the momentum vector. It should be noted that the numerical value for the momentum of a particle is arbitrary, as it depends in which frame of reference the velocity of the particle is defined. For example, your velocity with respect to the surface of the Earth is zero, so your momentum relative to the surface of the Earth is zero. However, relative to the surface of the Sun, your velocity, and momentum, are not zero. As we will see, forces are related to a changes in momentum, just as they are related to a change in velocity (acceleration).
If the particle has a constant mass, then the time derivative of its momentum is given by:
\[\begin{aligned} \frac{d}{dt}\vec p = \frac{d}{dt}m\vec v = m\frac{d}{dt}\vec v=m\vec a\end{aligned}\]
and we can write this as Newton’s Second Law, since \(m\vec a\) must be equal to the vector sum of the forces on the particle of mass \(m\):
\[\frac{d}{dt}\vec p =\sum\vec F=\vec F^{net}\]
The equation above is the original form in which Newton first developed his theory. It says that the net force on an object is equal to the rate of change of its momentum. If the net force on the object is zero, then its momentum is constant (as is its velocity). In terms of components, Newton’s Second Law written for the rate of change of momentum is given by:
\[\begin{aligned} \frac{dp_x}{dt} =& \sum F_x\\[4pt] \frac{dp_y}{dt} =& \sum F_y\\[4pt] \frac{dp_z}{dt} =& \sum F_z\end{aligned}\]
A particle of mass \(m\) is released from rest and allowed to fall freely under the influence of gravity near the Earth’s surface (assume that drag is negligible). Is the mechanical energy of the particle conserved? Is the momentum of the particle conserved? If momentum is not conserved, how does momentum change with time? Do your answers change if the force of drag cannot be ignored?
Solution
First, we model the falling particle assuming that there is no force of drag. The only force exerted on the particle is thus its weight.
The mechanical energy of the particle will be conserved only if there are no non-conservative forces doing work on the particle. Since the force of gravity is the only force acting on the particle, its mechanical energy is conserved.
The total momentum of the particle is not conserved, because the sum of the forces on the particle is not zero. Choosing the \(z\) axis to be vertical and positive upwards, Newton’s Second Law in the \(z\) direction is given by:
\[\begin{aligned} \sum F_z = -mg=\frac{dp_z}{dt}\end{aligned}\]
Note that the \(x\) and \(y\) components of momentum are conserved, since there are no forces with components in that direction. We can find how the \(z\) component of the momentum changes with time by taking the anti-derivative of the force with respect to time (from \(t=0\) to \(t=T\)):
\[\begin{aligned} \frac{dp_z}{dt} &= -mg\\[4pt] \int dp_z &= \int_0^T (-mg) dt\\[4pt] p_z(T) - p_z(0) &= -mgT\\[4pt] \therefore p_z(T) &= p_z(0) - mgT\end{aligned}\]
where the \(z\) component of momentum, \(p_z(T)\) at some time \(T\), is given by its value at time \(t=0\) plus \(-mgT\). If the object started at rest (\(\vec v=0\)), then the magnitude of the momentum, as a function of time, is given by:
\[\begin{aligned} p(t) = p_z(t) = -mgt\end{aligned}\]
and indeed changes with time.
If the force of drag were not negligible, there would be a non-conservative force acting on the particle, so its mechanical energy would no longer be conserved. The particle will accelerate until it reaches terminal velocity. During that phase of acceleration, the net force on the particle is not zero (it is accelerating), so its momentum is not conserved. Once the particle reaches terminal velocity, the net force on the particle is zero, and its momentum is conserved from then on.
Discussion
This simple example highlights the fact that mechanical energy and momentum are conserved under different conditions. Just because one is conserved does not mean that the other is conserved. It also shows that Newton’s Second Law is a statement about change in momentum, not momentum itself (just like it is a statement about acceleration, change in velocity, not velocity).
Impulse
When we introduced the concept of energy, we started by calculating the “work”, \(W\), done by a force exerted on an object over a specific path between two points:
\[\begin{aligned} W = \int_A^B \vec F \cdot d\vec l\end{aligned}\]
We then introduced kinetic energy, \(K\), to be that quantity whose change is equal to the net work done on the particle
\[\begin{aligned} W^{net} = \int_A^B \vec F^{net}\cdot d\vec l = \Delta K\end{aligned}\]
where the net force, \(\vec F^{net}\), is the vector sum of the forces on the particle.
We can do the same thing, but instead of integrating the force over distance, we can integrate it over time. We thus introduce the concept of “impulse”, \(\vec J\), of a force, as that force integrated from an initial time, \(t_A\), to a final time, \(t_B\):
\[\vec J = \int_{t_{A}}^{t_{B}}\vec F dt\]
where it should be clear that impulse is a vector quantity (and the above vector equation thus corresponds to one integral per component). Impulse is, in general, defined as an integral because the force, \(\vec F\), could change with time. If the force is constant in time (magnitude and direction), then we can define the impulse without using an integral:
\[\begin{aligned} \vec J = \vec F \Delta t\end{aligned}\]
where \(\Delta t\) is the amount of time over which the force was exerted. Although the force might never be constant, we can sometimes use the above formula to calculate impulse using an average value of the force.
What is the SI unit for impulse?
- \(\text{kg}\cdot \text{m/s}^{2}\)
- \(\text{kg} \cdot \text{s}^{2}\)
- \(\text{kg} \cdot \text{m/s}\)
- \(\text{kg} \cdot \text{m/s}^{3}\)
- Answer
Estimate the impulse that is given to someone’s head when they are slapped in the face.
Solution
When we slap someone’s face with our hand, our hand exerts a force on their face during the period of time, \(\Delta t\), over which our hand is in contact with their face. During that period of time, the force on their face goes from being \(0\), to some unpleasantly high value, and then back to zero, so the force cannot be considered constant.
Let us estimate the average magnitude of the slapping force by considering the deceleration of our slapping hand and modeling the motion as one-dimensional. Let us assume that our slapping hand has a mass \(m=1\text{kg}\) and that it is has a speed of \(2\text{m/s}\) just before it makes contact. Furthermore, let us assume that it is in contact with the face for a period of time \(\Delta t\). This allows us to find the average acceleration of our hand and thus the average force exerted by the face on our hand to stop it:
\[\begin{aligned} a &= \frac{\Delta v}{\Delta t}\\[4pt] \therefore F &= ma = m \frac{\Delta v}{\Delta t}\end{aligned}\]
By Newton’s Third Law, the force decelerating our hand has the same magnitude as the force that our hand exerts on the face, allowing us to calculate the impulse given to the person’s head:
\[\begin{aligned} J &= F\Delta t = \left(m \frac{\Delta v}{\Delta t}\right) \Delta t = m\Delta v\\[4pt] &=(1\text{kg})(2\text{m/s})=2\text{kg}\cdot \text{m/s}\end{aligned}\]
Discussion
Note that the impulse given to the head corresponds exactly to the change in momentum of the hand (\(\Delta p=m\Delta v\)).
So far, we calculated the impulse that is given by a single force. We can also consider the net impulse given to an object by the net force exerted on the object:
\[\begin{aligned} \vec J^{net} = \int_{t_A}^{t_B}\vec F^{net} dt\end{aligned}\]
Compare this to Newton’s Second Law written out using momentum:
\[\begin{aligned} \frac{d}{dt}\vec p &= \vec F^{net}\\[4pt] \int_{\vec p_A}^{\vec p_B} d\vec p &= \int_{t_A}^{t_B}\vec F^{net} dt\\[4pt] \vec p_B - \vec p_A &= \int_{t_A}^{t_B}\vec F^{net}dt\\[4pt] \therefore \Delta \vec p &= \int_{t_A}^{t_B}\vec F^{net} dt\end{aligned}\]
and we find that the net impulse received by a particle is precisely equal to its change in momentum:
\[\Delta\vec p = \vec J^{net}\]
This is similar to the statement that the net work done on an object corresponds to its change in kinetic energy, although one should keep in mind that momentum is a vector quantity, unlike kinetic energy.
A car moving with a speed of \(100\text{km/h}\) collides with a building and comes to a complete stop. The driver and passenger each have a mass of \(80\text{kg}\). The driver wore a seat belt that extended during the collision, so that the force exerted by the seatbelt on the driver acted for about \(2.5\text{s}\). The passenger did not wear a seat belt and instead was slowed down by the force exerted by the dashboard, over a much smaller amount of time, \(0.2\text{s}\). Compare the average decelerating force experienced by the driver and the passenger.
Solution
We can calculate the change in momentum of both people, which will be equal to the impulse they received as they collided with the seatbelt or with the dashboard. Since we know the duration in time that the forces were exerted, we can calculate the average force involved in order to give the required impulse. We can assume that this all happens in one dimension, so we use scalar quantities instead of vectors.
The change in momentum along the direction of motion for either the driver or passenger is given by:
\[\begin{aligned} \Delta p = p_B - p_A = (0)-p_A=-mv_A\end{aligned}\]
where \(v_A\) is the initial speed of the car, and the final momentum of either person is zero.
The change in momentum is equal to the impulse received by either person during a period of time \(\Delta t\), which is related to the force that was exerted on them:
\[\begin{aligned} J=F\Delta t &= \Delta p = -mv_A\\[4pt] F&=-m \frac{v_A}{\Delta t}\end{aligned}\]
For the driver, this corresponds:
\[\begin{aligned} F=(80\text{kg})\frac{(27.8\text{m/s})}{(2.5\text{s})}=890\text{N}\end{aligned}\]
and for the passenger:
\[\begin{aligned} F=(80\text{kg})\frac{(27.8\text{m/s})}{(0.2\text{s})}=11120\text{N}\end{aligned}\]
The force on the driver is thus comparable to their weight, whereas the passenger experiences an average force that is more than 10 times their weight.
Discussion
Any mechanism that results in a longer collision time will help to reduce the forces that are involved. This is why cars are designed to crumple in head-on collisions. We can understand this in terms of the crumpling of the car absorbing some of the kinetic energy of the car, as well as lengthening the time of the collision so that the forces involved are smaller. You may also hear people that look at modern cars that are all crumpled up after a crash and say something along the lines of “They sure don’t make cars the way they used to”. But of course, that is by design; it is safer if the car crumples up (and cars are designed to crumple up in specific areas, not the passenger cabin).
Note that we did not need to use impulse to calculate the average force, since we could have just used kinematics to determine the acceleration and Newton’s Second Law to calculate the corresponding force. Using impulse is equivalent by construction, but sometimes, it is easier mathematically.
Systems of particles: internal and external forces
So far, we have only used Newton’s Second Law to describe the motion of a single point mass particle or to describe the motion of an object whose orientation we did not need to describe (e.g. a block sliding down a hill). In this section, we consider what happens when there are multiple point particles that form a “system”.
In physics, we loosely define a system as the ensemble of objects/particles that we wish to describe. So far, we have only described systems made of one particle, so describing the motion of the system was equivalent to describing the motion of that single particle. A system of two particles could be, for example, two billiard balls on a pool table. To describe that system, we would need to provide functions that describe the positions, velocities, and forces exerted on both balls. We can also define functions/quantities that describe the system as a whole, rather than the details. For example, we can define the total kinetic energy of the system, \(K\), corresponding to the sum of kinetic energies of the two balls. We can also define the total momentum of the system, \(\vec P\), given by the vector sum of the momenta of the two balls.
When considering a system of multiple particles, we distinguish between internal and external forces. Internal forces are those forces that the particles in the system exert on each other. For example, if the two billiard balls in the system collide with each other, they will each exert a force on the other during the collision; those forces are internal. External forces are all other forces exerted on the particles of the system. For example, the force of gravity and the normal force from the pool table are both external forces exerted on the balls in the system (exerted by the Earth, or by the pool table, neither of which we considered to be part of the system). The force exerted by a person hitting one of the balls with a pool queue is similarly an external force. What we consider to be a system is arbitrary; we could consider the pool table and the Earth to be part of the system along with the two balls; in that case, the normal force and the weight of the balls would become internal forces. The classification of whether a force is internal or external to a system of course depends on what is considered part of the system.
Two pool balls crash against each other. Is this force of gravity exerted by one ball on the other an internal or external force?
- Internal.
- External.
- Answer
-
The key property of internal forces is that the vector sum of the internal forces in a system is zero. Indeed, Newton’s Third Law states that for every force exerted by object \(A\) on object \(B\), there is a force that is equal in magnitude and opposite in direction exerted by object \(B\) on object \(A\). If we consider both objects to be in the same system, then the sum of the internal forces between objects \(A\) and \(B\) must sum to zero. It is important to note that this is quite different than what we have discussed so far about summing forces. The forces that sum to zero are exerted on different objects. Thus far, we had only ever considered summing forces that are exerted on the same object in order to apply Newton’s Second Law. We have never encountered a situation where “action” and “reaction” forces are summed together, because they act on different objects.
Internal vs. External forces - what is the “system” and what forces should we consider?
As discussed above, internal and external forces can only be considered in the context of a specific system. So, how do we define this “system”? How far do we go when defining the system?
For example, let’s say that you kick a soccer ball, and it hits a nearby lawn chair, knocking it down. You want to determine what will happen to the soccer ball after it hits the lawn chair. What is defined to be the system here, and how should the forces be classified? Is the force exerted by the soccer ball on the lawn chair an external force? Should we consider the friction between the first foot particle that touches the first soccer ball particle?
The best way to approach “defining the system” is to pin down exactly what you’re trying to model. Here, specifically, you are trying to determine the velocity of the ball after it hits the lawn chair. In this situation, thinking about the friction between individual foot and soccer ball particles wouldn’t help us to figure out the final velocity of the soccer ball. Rather, thinking of the soccer ball and lawn chair as two giant, continuous particles, colliding and exchanging energy would be helpful. In this situation, it would be useful to consider the “system” to be the soccer ball and lawn chair only.
The force exerted by the soccer ball on the lawn chair would be an internal force, as this gives us information as to the final velocity of the soccer ball and is a force exchanged between the particles within the system. The force that gravity exerts on the lawn chair, normal force on the person’s foot and the force exerted by the foot on the soccer ball are all forces that we would consider “external”.
Remember - “internal” and “external” are not magical properties of a specific type of force. These definitions are made by us in the quest of building useful models.
Conservation of momentum
Consider a system of two particles with momenta \(\vec p_1\) and \(\vec p_2\). Newton’s Second Law must hold for each particle:
\[\begin{aligned} \frac{d\vec p_1}{dt}&=\sum_k \vec F_{1k}\\[4pt] \frac{d\vec p_2}{dt}&=\sum_k \vec F_{2k}\end{aligned}\]
where \(F_{ik}\) is the \(k\)-th force that is acting on particle \(i\). We can sum these two equations together:
\[\begin{aligned} \frac{d\vec p_1}{dt}+\frac{d\vec p_2}{dt} &= \sum_k \vec F_{1k} + \sum_k \vec F_{2k}\end{aligned}\]
The quantity on the right is the sum of the forces exerted on particle 1 plus the sum of the forces exerted on particle 2. In other words, it is the sum of all of the forces exerted on all of the particles in the system, which we can write as a single sum. On the left hand side, we have the sum of the two time derivatives of the momenta, which is equal to the time-derivative of the sum of the momenta. We can thus re-write the equation as:
\[\begin{aligned} \frac{d}{dt}(\vec p_1 + \vec p_2) = \sum \vec F\end{aligned}\]
where, again, the sum on the right is the sum over all of the forces exerted on the system. Some of those forces are external (e.g. gravity exerted by Earth on the particles), whereas some of the forces are internal (e.g. a contact force between the two particles). We can separate the sum into a sum over all external forces (\(\vec F^{ext}\)) and a sum over internal forces (\(\vec F^{int}\)):
\[\begin{aligned} \sum \vec F = \sum \vec F^{ext} + \sum \vec F^{int} \end{aligned}\]
The sum of the internal forces is zero:
\[\begin{aligned} \sum \vec F^{int} = 0\end{aligned}\]
because for every force that particle 1 exerts on particle 2, there will be an equal and opposite force exerted by particle 2 on particle 1. We thus have:
\[\begin{aligned} \frac{d}{dt}(\vec p_1 + \vec p_2) = \sum \vec F^{ext}\end{aligned}\]
Furthermore, if we introduce the “total momentum of the system”, \(\vec P=\vec p_1 + \vec p_2\), as the sum of the momenta of the individual particles, we find:
\[\begin{aligned} \frac{d\vec P}{dt} &= \sum \vec F^{ext}\end{aligned}\]
which is the equivalent of Newton’s Second Law for a system where, \(\vec P\), is the total momentum of the system, and the sum of the forces is only over external forces to the system.
Note that the derivation above easily extends to any number, \(N\), of particles, even though we only did it with \(N=2\). In general, for the “ith particle”, with momentum \(\vec p_i\), we can write Newton’s Second Law:
\[\begin{aligned} \frac{d\vec p_i}{dt}=\sum_k \vec F_{ik}\end{aligned}\]
where the sum is over only those forces exerted on particle \(i\). Summing the above equation for all \(N\) particles in the system:
\[\begin{aligned} \frac{d}{dt}\sum_i \vec p_i=\sum \vec F^{ext} + \sum \vec F^{int}\end{aligned}\]
where the sum over internal forces will vanish for the same reason as above. Introducing the total momentum of the system, \(\vec P\):
\[\begin{aligned} \vec P = \sum_i \vec p_i\\[4pt]\end{aligned}\]
We can write an equation for the time-derivative of the total momentum of the system:
\[\frac{d\vec P}{dt}=\sum\vec F^{ext}\]
where the sum of the forces is the sum over all forces external to the system. Thus, if there are no external forces on a system, then the total momentum of that system is conserved (if the time-derivative of a quantity is zero then that quantity is constant).
We already argued in the previous section that we can make all forces internal if we choose our system to be large enough. If we make the system be the Universe, then there are no forces external to the Universe, and the total momentum of the Universe must be constant:
\[\begin{aligned} \frac{d\vec P^{Universe}}{dt} &= \sum_{Universe} \vec F^{ext} = 0 \\[4pt] \therefore \vec P^{Universe}&=\text{constant}\end{aligned}\]
In summary, we saw that:
- If no forces are exerted on a single particle, then the momentum of that particle is constant (conserved).
- In a system of particles, the total momentum of the system is conserved if there are no external forces on the system.
- If there are no non-conservative forces exerted on a particle, then that particle’s mechanical energy is constant (conserved).
- In a system of multiple particles, the total mechanical energy of the system will be conserved if there are no non-conservative forces exerted on the system.
When we refer to a force being “exerted on a system”, we mean exerted on one or more of the particles in the system. In particular, the sum of the work done by internal forces is not necessarily zero, so energy and momentum are thus conserved under different conditions.
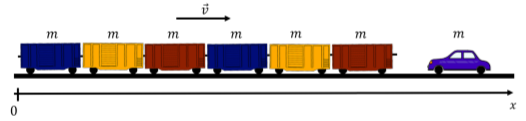
Consider a train made of \(N\) cars of equal mass \(m\) that is traveling at constant speed \(v\) along a straight piece of track where friction and drag are negligible, as depicted in Figure \(\PageIndex{1}\). An empty car of mass \(m\) was left at rest on the track in front of the train. The train collides with the empty car which stays attached to the front of the train. What is the speed of the train after the collision? Is the total mechanical energy of the system conserved?
Solution
When the train collides with the car, it will exert a “collision” force on the car, and the car will exert an opposite force on the train. If we consider both of the train and the car as being part of the same system, then those collision forces will be internal, and the momentum of the system (train + car) will be conserved. The train and car both experience external forces from Earth’s gravity and the normal force from the train tracks. However, those two sets of forces cancel each other out, since neither the train nor the car have any acceleration in the vertical direction (the sum of the forces on each object has no net vertical component). Thus, there are no net external forces on the car+train system, and the total momentum of the system is conserved through the collision.
We can model this system in one dimension (along the track), defining our \(x\) axis. We choose the ground as a frame of reference, the positive direction parallel to the initial velocity of the train, and the origin to be located where the car initially starts. Before the collision, the \(x\) component of the momenta of the train (mass \(Nm\)) and car (mass \(m\)) are:
\[\begin{aligned} p_{train}&=Nmv\\[4pt] p_{car}&=0\end{aligned}\]
After the collision, the car is attached to the train (and thus has the same speed, \(v'\)), so the momenta of the train and car after the collision are:
\[\begin{aligned} p'_{train}&=Nmv'\\[4pt] p'_{car}&=mv'\end{aligned}\]
where the primes \('\) denote quantities after the collision. Applying conservation of momentum to the system, the total momentum before and after the collision must be equal:
\[\begin{aligned} p_{train}+p_{car}&=p'_{train}+p'_{car}\\[4pt] \therefore Nmv &= Nmv' +mv'\\[4pt] \therefore v' &=\frac{N}{N+1}v\end{aligned}\]
and the speed of the train with the additional car attached is reduced by a factor \(N/(N+1)\) compared to what it was before the collision.
We can check to see if the mechanical energy of the system is conserved, since we know the speeds of the train and car before and after the collision. Since all of the motion is horizontal, gravity and the normal force do no work on either the train or car, so their mechanical energy can be taken as their kinetic energy (their gravitational potential energy does not change after the collision). The total mechanical energy of the system, \(E\), before the collision is the kinetic energy of the train:
\[\begin{aligned} E= \frac{1}{2}Nmv^2\end{aligned}\]
The total mechanical energy of the system, \(E'\), after the collision is:
\[\begin{aligned} E' &= \frac{1}{2}Nmv'^2 + \frac{1}{2}mv'^2 = \frac{1}{2}(N+1)mv'^2 \\[4pt] &=\frac{1}{2}(N+1)m \left( \frac{N}{N+1}v \right)^2\\[4pt] &=\frac{1}{2}m\frac{N^2}{N+1}v^2\end{aligned}\]
and we see that \(E'<E\), and thus that the total mechanical energy of the system is not conserved (it is reduced after the collision).
Discussion
We could have solved this problem by carefully modeling the force exerted by the car on the train during the collision, which would have allowed us to find the speed of the train after the collision using its acceleration. This would have required a detailed model for that force, which we do not have. However, by realizing that the train and car could be considered as a system with no net external forces exert on it, we were able to easily find the speed of the train after the collision using conservation of momentum.
We also found that mechanical energy was not conserved. This makes physical sense because, for the car to remain attached to the train, there presumably had to be some significant forces in play that “crushed” the car into the train. Some of the initial kinetic energy of the train was used to deform the train and the car during the collision. We can also think of deforming a material as giving it energy. Sometimes that energy is recoverable (e.g. compressing a spring), sometimes, it is not (e.g. crushing a car).
If the car and train were equipped with large springs to absorb the energy of the impact, the collision could have conserved mechanical energy, as the springs compress and then expand back. The speed of the car and train would then be different after the collision in this case (see Example 10.2.3). It is a feature of collisions where the two bodies remain attached to each other that mechanical energy is not conserved.