10.2: Collisions
- Page ID
- 19430
In this section we go through a few examples of applying conservation of momentum to model collisions. Collisions can loosely be defined as events where the momenta of individual particles in a system are different before and after the event.
We distinguish between two types of collisions: elastic and inelastic collisions. Elastic collisions are those for which the total mechanical energy of the system is conserved during the collision (i.e. it is the same before and after the collision). Inelastic collisions are those for which the total mechanical energy of the system is not conserved. In either case, to model the system, one chooses to define the system such that there are no external forces on the system so that total momentum is conserved.
Inelastic collisions
In this section, we give a few examples of modelling inelastic collisions. Inelastic collisions are usually easier to handle mathematically, because one only needs to consider conservation of momentum and does not use conservation of energy (which usually involves equations that are quadratic in the speeds because of the kinetic energy term).
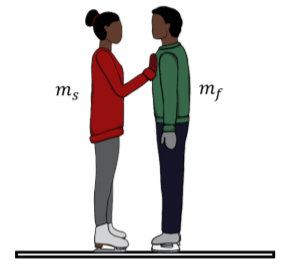
You (mass \(m_s\)) and your friend (mass \(m_f\)) face each other on ice skates on an ice surface that is slippery enough that friction can be considered negligible, as shown in Figure \(\PageIndex{1}\). You shove your friend away from you so that he moves with velocity \(\vec v_f\) away from you (the velocity is measured relative to the ice). Is the collision elastic? What is your speed relative to the ice after you shoved your friend?
Solution
We can consider the system as being comprised of you and your friend. There are no net external forces on the system (gravity and normal forces cancel each other), so the momentum of the system will be conserved.
The mechanical energy will not be conserved. You had to use chemical potential energy stored in your muscles to shove your friend. Thus, external energy (i.e. not mechanical energy from you or your friend) was injected into the system, and we should expect the total mechanical energy to be larger after the collision.
Before the collision, both you and your friend have zero speed, and thus zero kinetic energy and zero momentum. After the collision, your friend has a velocity \(\vec v_f\). We can use conservation of total momentum, \(\vec P\), to determine your velocity, \(\vec v_s\), after the collision.
\[\begin{aligned} \vec P &=\vec P'\\[4pt] 0 &= m_s\vec v_s + m_f\vec v_f\\[4pt] \therefore \vec v_s &= -\frac{m_f}{m_s}\vec v_f\end{aligned}\]
where primes (\('\)) denote a quantity after the collision. We find that your velocity is in the opposite direction from that of your friend. Before the collision, the mechanical energy, \(E\), of the system is zero (we can ignore gravitational potential energy, since everything is in the horizontal plane). After the collision, the mechanical energy, \(E'\), is:
\[\begin{aligned} E' = \frac{1}{2}m_sv_s^2+\frac{1}{2}m_fv_f^2\end{aligned}\]
which is clearly bigger than the mechanical energy before the collision (i.e. 0), as we suspected it would be.
Discussion
We find that you recoil in the opposite direction, which makes sense. If you push your friend in one direction, Newton’s Third Law says that your friend pushes you in the opposite direction. Your speed furthermore depends on the ratio of your friend’s mass to yours. This also makes sense, because if you both feel the same force, the person with the smallest mass will have the highest speed; if your mass is higher than your friend’s, then your speed after the collision will be smaller than your friend’s.
We also saw that mechanical energy was not conserved. In terms of energy, we can explain this by saying that you burned up chemical potential energy stored in your muscles in order to shove your friend. Because we included both you and your friend in the system, the shove was an internal force and momentum is conserved. Of course, if we had considered only you as the system, then your momentum would not have been conserved during the collision.
The type of collision that we described here is also sometimes called an “explosion”. You can imagine all of the parts that make up a bomb as small particles. When the bomb explodes, chemical potential energy is converted into the kinetic energy of the bomb fragments. If you consider all of the particles/fragments of the bomb as a system, then the total momentum of all of the bomb fragments is conserved (and equal to zero if the bomb was initially at rest). Again, mechanical energy would not be conserved (and would increase) as the chemical potential energy is converted into mechanical energy.
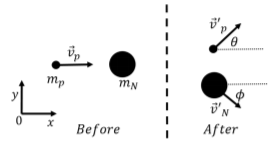
A proton of mass \(m_p\) and initial velocity \(\vec v_p\) collides inelastically with a nucleus of mass \(m_N\) at rest, as shown in Figure \(\PageIndex{2}\). A coordinate system is set up as shown, such that the initial velocity of the proton is in the \(x\) direction. After the collision, the proton’s speed is measured to be \(v'_p\) and its velocity vector is found to make an angle \(\theta\) with the \(x\) axis as shown. What is the velocity vector of the nucleus after the collision? Assume that the collision takes place in vacuum.
Solution
As a system, we consider the proton and the nucleus together, so that the total momentum of the system is conserved during the collision, as no other external forces are exerted on the two particles (since they are in vacuum). Because momentum is a vector, each component of the total momentum, \(\vec P\), is conserved during the collision:
\[\begin{aligned} \vec P &= \vec P'\\[4pt] \therefore P_x &= P'_x\\[4pt] \therefore P_y &= P'_y\end{aligned}\]
where, as usual, primes (\('\)) denote quantities after the collision. After the collision, both particles will have velocity vectors that have \(x\) and \(y\) components. Let the velocity vector of the nucleus after the collision be \(\vec v'_N\) and let \(\phi\) be the angle that it makes with the \(x\) axis, as shown in Figure \(\PageIndex{2}\).
We can start by considering the conservation of the \(x\) component of the total momentum. The initial and final momenta in the \(x\) direction are given by:
\[\begin{aligned} P_x &= m_p v_p\\[4pt] P'_x &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\\[4pt] \therefore m_p v_p &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\end{aligned}\]
which gives us a first equation to determine the final velocity of the nucleus.
The \(y\) component of the total momentum before the collision is zero since we chose the coordinate system such that the initial velocity of the proton is in the \(x\) direction. The initial and final momenta in the \(y\) direction are given by:
\[\begin{aligned} P_y &= 0\\[4pt] P'_y &= m_p v'_p\sin\theta - m_N v'_N\sin\phi\\[4pt] \therefore m_p v'_p\sin\theta &= m_N v'_N\sin\phi\end{aligned}\]
which gives us a second equation to solve for the velocity of the nucleus. With the two equations from momentum conservation, we can solve for the magnitude and direction of the velocity of the nucleus. From the \(y\) component of momentum conservation, we can find an expression for the speed of the nucleus:
\[\begin{aligned} m_p v'_p\sin\theta &= m_N v'_N\sin\phi\\[4pt] \therefore v'_N &= \frac{m_p}{m_N}v'_p\sin\theta \frac{1}{\sin\phi}\end{aligned}\]
which we can substitute into the \(x\) equation for momentum conservation to solve for the angle \(\phi\):
\[\begin{aligned} m_p v_p &= m_p v'_p\cos\theta + m_N v'_N\cos\phi\\[4pt] m_p v_p &= m_p v'_p\cos\theta + m_N\frac{m_p}{m_N}v'_p\sin\theta \frac{\cos\phi}{\sin\phi} \\[4pt] v_p &= v'_p\cos\theta + v'_p\sin\theta \frac{1}{\tan\phi}\\[4pt] \therefore \tan\phi &= \frac{v'_p\sin\theta}{v_p-v'_p\cos\theta}\end{aligned}\]
If we were given numbers for the initial and final speed of the proton, as well as the angle \(\theta\), we would be able to find a value for the angle \(\phi\), which we could then use to determine the final speed of the nucleus:
\[\begin{aligned} v'_N &= \frac{m_p}{m_N}v'_p\sin\theta \frac{1}{\sin\phi}\end{aligned}\]
Discussion:
By using the conservation of momentum equation and writing out the \(x\) and \(y\) components, we were able to find two equations to determine the magnitude and direction of the nucleus’ velocity after the collision. In the limit where \(m_N >> m_p\), the final speed of the nucleus would be very small (close to zero).
Elastic collisions
In this section, we give a few examples of modeling elastic collisions. Even though it is mechanical energy that is conserved in an elastic collision, one can almost always simplify this to only kinetic energy being conserved. If a collision takes place in a well localized position in space (i.e. before and after the collision are the same point in space), then the potential energies of the objects involved will not change, thus any change in their mechanical energy is due to a change in kinetic energy.
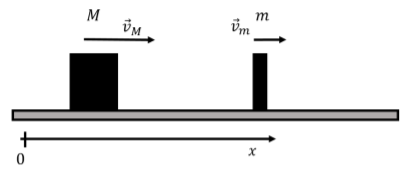
A block of mass \(M\) moves with velocity \(\vec v_M\) in the \(x\) direction, as shown in Figure \(\PageIndex{3}\). A block of mass \(m\) is moving with velocity \(\vec v_m\) also in the \(x\) direction and collides elastically with block \(M\). Both blocks slide with no friction on the horizontal surface. What are the velocities of the two blocks after the collision?
Solution
Because this is an elastic collision, both the total momentum and total mechanical energy are conserved. Equating the total momentum before and after the collision, and considering only the \(x\) component gives the following equation:
\[\begin{aligned} \vec P &=\vec P'\\[4pt] Mv_M+mv_m&=Mv'_M+mv'_m\end{aligned}\]
where the primes (\('\)) correspond to the quantities after the collision. Note that, in principle, the \(x\) components of the velocities (\(v_M\), \(v'_M\), \(v_m\), \(v'_m\)) could be negative numbers if the corresponding block is moving in the negative \(x\) direction.
For the mechanical energy of the two blocks, we only need to consider their kinetic energy since their gravitational potential energies are the same before and after the collision on the horizontal surface. The total mechanical energy of the system, before and after the collision is given by:
\[\begin{aligned} E &=E'\\[4pt] \frac{1}{2}Mv_M^2+\frac{1}{2}mv_m^2&=\frac{1}{2}Mv'^2_M+\frac{1}{2}mv'^2_m\\[4pt] \therefore Mv_M^2+mv_m^2&=Mv'^2_M+mv'^2_m\end{aligned}\]
where we canceled the factor of one half in the last line. This gives two equations (conservation of energy and momentum) and two unknowns (the two speeds after the collision). This is not a linear system of equations, because the equation from conservation of energy is quadratic in the speeds.
The following method allows many models for elastic collisions between two particles to be solved easily by converting the quadratic equation from energy conservation into an equation that is linear in the speeds. First, write both equations so that the quantities related to each particle are on opposite sides of the equation. For momentum, this gives:
\[Mv_{M}+mv_{m}=Mv_{M}^{'} +mv_{m}^{'}\]
\[\therefore M(v_{M}-v_{M}^{'})=m(v'm-v_{m})\]
For conservation of energy, this gives:
\[Mv_{M}^{2}+mv_{m}^{2}=Mv_{M}^{'2}+mv_{m}^{'2}\]
\[\therefore M(v_{M}^{2}-v_{M}^{'2}=M(v_{m}^{'2}-v_{m}^{2})\]
which we can re-write as:
\[\begin{aligned} M(v_M^2-v'^2_M)&= M(v'^2_m-v^2_m)\\[4pt] M(v_M-v'_M)(v_M+v'_M)&= M(v'_m-v_m)(v'_m+v_m)\end{aligned}\]
We can then divide Equation 10.2.3 and 10.2.4 by Equation 10.2.1 and 10.2.2:
\[\begin{aligned} \frac{M(v_M-v'_M)(v_M+v'_M)}{M(v_M-v'_M)}&= \frac{M(v'_m-v_m)(v'_m+v_m)}{m(v'm-v_m)}\\[4pt] \therefore v_M+v'_M&=v'_m+v_m\end{aligned}\]
which gives us an equation that is much easier to work with, since it is linear in the speeds. If we re-arrange this last equation back so that quantities before and after the collision are on different sides of the equality:
\[v_{M}-v_{m}=-(v_{M}^{'}-v_{m}^{'})\]
we can see that the relative speed between \(M\) and \(m\) is the same before and after the collision. That is, if block \(M\) “saw” block \(m\) approaching with a speed of \(3\text{m/s}\) before the collision, it would “see” block \(m\) moving away with speed \(3\text{m/s}\) after the collision, regardless of the actual directions and velocities of the block, if the collision was elastic.
By using this equation with the original conservation of momentum equation, we now have two equations and two unknowns that are easy to solve:
\[\begin{aligned} v_M-v_m &= - (v'_M-v'_m)\\[4pt] Mv_M+mv_m&=Mv'_M+mv'_m\end{aligned}\]
Solving for \(v'_m\) in both equations gives:
\[\begin{aligned} v_M-v_m &= - (v'_M-v'_m)\\[4pt] \therefore v'_m &= v_M+v'_M-v_m\\[4pt] Mv_M+mv_m&=Mv'_M+mv'_m\\[4pt] \therefore v'_m&=\frac{1}{m}(Mv_M+mv_m-Mv'_M)\end{aligned}\]
Equating the two expressions for \(v'_m\) allows us to solve for \(v'_M\):
\[\begin{aligned} \frac{1}{m}(Mv_M+mv_m-Mv'_M)&=v_M+v'_M-v_m\\[4pt] Mv_M+mv_m-Mv'_M&=mv_M+mv'_M-mv_m\\[4pt] (M-m)v_M+2mv_m&=(M+m)v'_M\\[4pt] \therefore v'_M&=\frac{M-m}{M+m}v_M+\frac{2m}{M+m}v_m\end{aligned}\]
One can easily solve for the other speed, \(v'_m\):
\[\begin{aligned} \therefore v'_m &= \frac{m-M}{M+m}v_m+\frac{2M}{M+m}v_M\end{aligned}\]
And writing these together:
\[\begin{aligned} v'_M&=\frac{M-m}{M+m}v_M+\frac{2m}{M+m}v_m\\[4pt] v'_m &= \frac{m-M}{M+m}v_m+\frac{2M}{M+m}v_M\end{aligned}\]
Discussion
The formulas that we obtained above are valid for any one dimensional elastic collision.
Two trains of equal masses collide elastically on a track. If train \(A\) had a speed \(v\) and train \(B\) was at rest, what are the speeds of the trains after the collision?
- Both trains \(A\) and \(B\) travel away from each other with speeds \(\frac{1}{2}v\).
- Train \(A\) will be at rest and train \(B\) will move away with a speed \(v\).
- Both trains \(A\) and \(B\) will stick together and move at a speed of \(v\).
- Train \(B\) will be at rest and train \(A\) will move away at a speed of \(v\).
- Answer
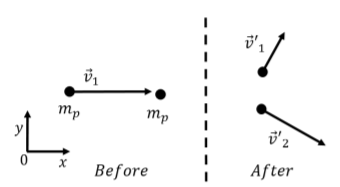
A proton of mass \(m\) and initial velocity \(\vec v_1\) collides elastically with a second proton that is at rest. After the collision, the two protons have velocities \(\vec v'_1\) and \(\vec v'_2\), as shown in Figure \(\PageIndex{4}\). Show that the velocity vectors of the two protons are perpendicular after the collision.
Solution
This example highlights a particular feature of elastic collisions when the two objects have the same mass and one of the objects is initially at rest. The conservation of momentum for the system comprised of the two protons can be written as:
\[\begin{aligned} m\vec v_1 &= m\vec v'_1 + m\vec v'_2\\[4pt] \vec v_1 &= \vec v'_1 + \vec v'_2\end{aligned}\]
where the left hand side corresponds to the initial total momentum and the right hand side to the total momentum after the collision. In the second line, we canceled out the mass, and obtained a vector relation between the velocity vectors. We can graphically illustrate the vector relation as in Figure \(\PageIndex{5}\) which shows the triangle that is formed by adding the two outgoing velocity vectors to obtain the initial velocity vector.
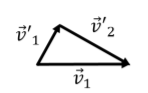
Conservation of kinetic energy for the collision can be written as:
\[\begin{aligned} \frac{1}{2}mv_1^2 &= \frac{1}{2}mv'^2_1+\frac{1}{2}mv'^2_2\\[4pt] v_1^2 &= v'^2_1+ v'^2_2\end{aligned}\]
where the left hand side corresponds to the initial kinetic energy and the right hand side to the final kinetic energy. We canceled the mass and factor of one half in the second line. This last equation gives a relation between the magnitudes of the velocity vectors. By comparing the equation above to Pythagoras’ theorem, and by inspecting the triangle in Figure \(\PageIndex{5}\), it is clear that the triangle must be a right angle triangle, and thus that \(\vec v'_1\) and \(\vec v'_2\) must be perpendicular.
Frames of reference
Before proceeding, you may wish to review Sections 3.4 and 4.1 on expressing velocities in different frames of reference.
Because the momentum of a particle is defined using the velocity of the particle, its value depends on the reference frame in which we chose to measure that velocity. In some cases, it is useful to apply momentum conservation in a frame of reference where the total momentum of the system is zero. For example, consider two particles of mass \(m_1\) and \(m_2\), moving towards each other with velocities \(\vec v_1\) and \(\vec v_2\), respectively, as measured in a frame of reference \(S\), as illustrated in Figure 10.2.6.
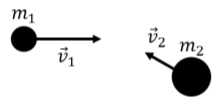
In the frame of reference \(S\), the total momentum, \(\vec P\), of the two particles can be written:
\[\begin{aligned} \vec P = m_1\vec v_1 + m_2\vec v_2\end{aligned}\]
Consider a frame of reference, \(S'\), that is moving with velocity, \(\vec v_{CM}\), relative to the frame of reference \(S\). In that frame of reference, the velocities of the two particles are different and given by:
\[\begin{aligned} \vec v'_1&=\vec v_1- \vec v_{CM}\\[4pt] \vec v'_2&=\vec v_2- \vec v_{CM}\end{aligned}\]
The total momentum, \(\vec P'\), in the frame of reference \(S'\) is then given by1:
\[\begin{aligned} \vec P' &= m_1\vec v'_1 + m_2 \vec v'_2\\[4pt] &=m_1(\vec v_1- \vec v_{CM})+m_2(\vec v_2- \vec v_{CM})\\[4pt] &= m_1\vec v_1 + m_2\vec v_2 - (m_1+m_2) \vec v_{CM}\end{aligned}\]
We can choose the velocity of the frame \(S'\), \(\vec v_{CM}\), such that the total momentum in that frame of reference is zero:
\[\begin{aligned} \vec P' &= 0\\[4pt] m_1\vec v_1 + m_2\vec v_2 - (m_1+m_2) \vec v_{CM} &=0\\[4pt] \therefore \vec v_{CM} &= \frac{m_1\vec v_1 + m_2\vec v_2 }{m_1+m_2}\end{aligned}\]
This “special” frame of reference, in which the total momentum of the system is zero, is called the “center of mass frame of reference”. The velocity of center of mass frame of reference can easily be obtained if there are \(N\) particles involved instead of two:
\[\therefore \vec v_{CM}=\frac{m_{1}\vec v_{1}+m_{2}\vec v_{2}+m_{3}\vec v_{3}+...}{m_{1}+m_{2}+m_{3}+...}=\frac{\sum m_{i}\vec v_{i}}{\sum m_{i}}\]
Again, you should note that because the above equation is a vector equation, it represents one equation per component of the vectors. For example, the \(x\) component of the velocity of the center of mass frame of reference is given by:
\[\begin{aligned} \therefore v_{CMx} = \frac{m_1 v_{1x} + m_2v_{2x} + m_3 v_{3x} + \dots }{m_1+m_2+m_3+\dots}=\frac{\sum m_iv_{ix}}{\sum m_i}\end{aligned}\]
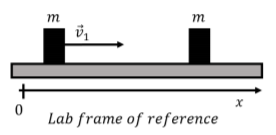
In the frame of reference of a lab, a block of mass \(m\) has a velocity \(\vec v_1\) directed along the positive \(x\) axis and is approaching a second block of mass \(m\) that is at rest (\(\vec v_2=0\)), as shown in Figure \(\PageIndex{7}\). What is the velocity of the center of mass frame? What is the velocity of each block in the center of mass frame? Verify that the total momentum is zero in the center of mass frame.
Solution
Since this is a one dimensional situation, we only need to evaluate the \(x\) component of the velocity of the center of mass:
\[\begin{aligned} \vec v_{CM} &= \frac{m_1\vec v_1 + m_2\vec v_2 }{m_1+m_2}\\[4pt] \therefore v_{CMx} &= \frac{m_1 v_{1x} + m_2 v_{2x}}{m_1+m_2}\\[4pt] &=\frac{mv_1 + m(0) }{m+m}\\[4pt] &=\frac{1}{2}v_1\end{aligned}\]
The center of mass frame of reference is thus also moving along the positive direction of the \(x\) axis, but with a speed that is half of that of the moving block. In the center of mass frame of reference, it appears that the block on the left is slower than in the lab frame and that the block on the right is moving in the negative \(x\) direction. The velocities of the two blocks in the center of mass frame of reference are given by:
\[\begin{aligned} v'_1&=v_1-v_{CMx}=\frac{1}{2}v_1\\[4pt] v'_2&=(0)-v_{CMx}=-\frac{1}{2}v_1\end{aligned}\]
Thus, in the reference frame of the center of mass, the two block are approaching each other with the same speed (\(v_1/2\)), which is only the case because the two blocks have the same mass. The blocks, as viewed in the center of mass frame of reference, are shown in Figure \(\PageIndex{8}\).
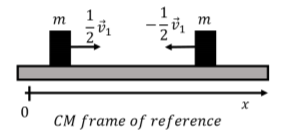
Clearly, the total momentum is zero in the center of mass frame of reference:
\[\begin{aligned} \vec P' = m\vec v'_1+ m\vec v'_2 = m \left(\frac{1}{2}\vec v_1 - \frac{1}{2}\vec v_1\right) = 0\end{aligned}\]
Discussion
As we have seen, in the center of mass frame of reference the total momentum is zero. If there are only two particles, and they have the same mass, then, in the center of mass frame of reference, they both have the same speed and move either towards or away from each other.
Footnotes
1. Note that we are using primes (\('\)) to denote quantities in a different reference frame, not after a collision.