10.6: Sample problems and solutions
- Page ID
- 19434
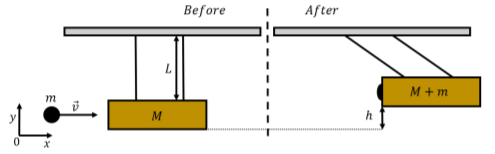
A ballistic pendulum is a device that can be built to measure the speed of a projectile. The pendulum is constructed such that the projectile is fired at the bob of the pendulum (typically a block of wood) which then swings as illustrated in Figure \(\PageIndex{1}\), with the projectile embedded within. By measuring the height that is reached by the pendulum’s bob, one can determine the speed of the projectile before it collided with the pendulum. If a ballistic pendulum with a mass \(M\) suspended at the end of strings of length \(L\) is observed to rise by a height \(h\) after being struck by a bullet of mass \(m\), how fast was the bullet moving?
- Answer
-
We can model this situation by dividing it into three phases:
- Before the bullet collides with the pendulum, only the bullet has momentum in the \(x\) direction.
- Immediately after the inelastic collision, the bullet and pendulum form a combined object of mass \(M+m\) that has the same momentum as the bullet, in the \(x\) direction, before the pendulum starts to swing upwards.
- The pendulum with the embedded bullet swings upwards until its kinetic energy is zero.
The collision between the bullet and pendulum is inelastic, because some of the kinetic energy of the bullet is used to deform the bullet and the pendulum. In general, any collision where two objects end up “stuck together” is inelastic.
In order to model the pendulum’s motion we first apply conservation of momentum to determine the speed, \(v'\), of the pendulum and embedded bullet just after the collision. Applying conservation of momentum in the \(x\) direction to the system formed by the pendulum and the bullet, just before and after the collision, we have:
\[\begin{aligned} P&=mv \\[4pt] P'&=(M+m)v' \\[4pt] \therefore mv&=(M+m)v' \\[4pt] \therefore v' &=\frac{m}{m+M}v \end{aligned}\]
where \(P\) and \(P'\) are the initial and final momenta of the system, respectively. The pendulum with the bullet embedded in it will thus have a speed of \(v'\) at the bottom of the pendulum’s motion, before it swings upwards.
We can now use conservation of energy to model the swinging motion since, at that point, only tension and gravity act on the pendulum, and there are no non-conservative forces. If we choose the origin to be the location of the pendulum at the bottom of its trajectory, its initial gravitational potential energy is zero and its initial mechanical energy, \(E\), is given by:
\[\begin{aligned} E = \frac{1}{2}(m+M) v'^2 \end{aligned}\]
At the top of the trajectory, the pendulum with the embedded bullet will stop and have no kinetic energy. The mechanical energy at the top of the trajectory, \(E'\), is thus equal to the gravitational potential energy of the pendulum at a height \(h\) above the origin:
\[\begin{aligned} E' = (m+M)gh\end{aligned}\]
Applying conservation of mechanical energy allows us to find the initial speed of the bullet:
\[\begin{aligned} E &= E'\\[4pt] \frac{1}{2}(m+M) v'^2 &= (m+M)gh\\[4pt] v'^2 &= 2gh\\[4pt] \left( \frac{m}{m+M}v\right)^2&= 2gh\\[4pt] \therefore v &= \frac{m+M}{m} \sqrt{2gh}\end{aligned}\]
where is the second last line we used the expression for \(v'\) that we obtained from conservation of momentum.
Discussion
This example showed a situation in which momentum and energy were both conserved, but not at the same time. This example also highlighted how, by using conservation laws, one can derive models that are much easier to solve mathematically than if one had to model all of the forces involved.
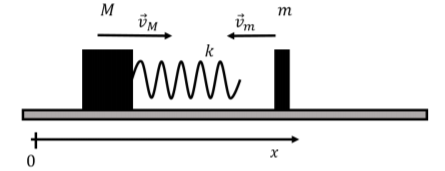
A block of mass \(M\) with a spring of spring constant \(k\) attached to it is sliding on a frictionless surface with velocity \(\vec v_M\) in the \(x\) direction. A second block of mass \(m\) has velocity \(\vec v_m\) also in the \(x\) direction (shown above in the negative \(x\) direction, but let us assume that we do not necessarily know the direction, only that the two blocks will collide). During the collision between the blocks, what is the maximum amount by which the spring is compressed?
- Answer
-
The collision is elastic because the energy used to compress the spring is “given back” when the spring extends again, since the spring force is conservative.
They key to modeling the compression of the spring is to identify the condition under which the spring is maximally compressed. This will occur at the point during the collision where the two masses will have exactly the same velocity, momentarily moving in unison as the spring is maximally compressed. Because, instantaneously, the masses have the same velocity, there is a frame of reference in which the two masses are at rest, and the momentum is zero. Of course, that frame of reference is the center of mass frame of reference.
Because the collision is one-dimensional, we can calculate the velocity of the center of mass as:
\[\begin{aligned} v_{CM} = \frac{Mv_M+mv_m}{m+M}\end{aligned}\]
where we note that \(v_m\) is a negative number, since the block of mass \(m\) is moving in the negative \(x\) direction. The total momentum, \(\vec P^{CM}\), in the center of mass frame of reference must be zero. Writing this out for the \(x\) component and transforming the velocities of the two blocks into the center of mass frame of reference:
\[\begin{aligned} P^{CM}_x = M(v_M-v_{CM})+m(v_m-v_{CM})&=0\\[4pt] \therefore (v_m-v_{CM}) &= -\frac{M}{m}(v_M-v_{CM})\end{aligned}\]
Also note that we can write the velocity difference \(v_M-v_{CM}\) without using the center of mass velocity:
\[\begin{aligned} v_M-v_{CM} &= v_M-\frac{Mv_M+mv_m}{m+M}=\frac{1}{m+M}(v_M(m+M)-Mv_M-mv_m)\\[4pt] &=\frac{m}{m+M}(v_M-v_m)\end{aligned}\]
We can then use conservation of energy in the center of mass frame to determine the maximal compression of the spring. Before the collision, the total mechanical energy in the system, \(E\), is the sum of the kinetic energies of the two blocks (as the spring is not compressed):
\[\begin{aligned} E&=\frac{1}{2}m(v_m-v_{CM})^2+\frac{1}{2}M(v_M-v_{CM})^2\\[4pt] &=\frac{1}{2}\frac{M^2}{m}(v_M-v_{CM})^2+\frac{1}{2}M(v_M-v_{CM})^2\\[4pt] &=\frac{1}{2}M \left( 1 + \frac{M}{m}\right) (v_M-v_{CM})^2\\[4pt] &=\frac{1}{2}M \left(\frac{m+M}{m} \right)(v_M-v_{CM})^2\\[4pt] &=\frac{1}{2}M \left(\frac{m+M}{m} \right)\left(\frac{m}{m+M}(v_M-v_m)\right)^2\\[4pt] &=\frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2\end{aligned}\]
where we used our expressions above to simplify the expression. When the spring is maximally compressed, the two blocks are at rest and the mechanical energy of the system, \(E'\), is all “stored” as spring potential energy:
\[\begin{aligned} E'&=\frac{1}{2}kx^2\end{aligned}\]
where \(x\) is the distance by which the spring is compressed. Equating the two allows us to determine the maximal compression of the spring:
\[\begin{aligned} E &= E' \\[4pt] \frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2 &= \frac{1}{2}kx^2\\[4pt] \therefore x &= \sqrt{\frac{1}{k} \left(\frac{mM}{m+M}\right)}(v_M-v_m)\end{aligned}\]
Discussion
By modeling the collision in the center of mass frame of reference, we were easily able to determine the maximal compression of the spring. This would have been more difficult in the lab frame of reference, because the two blocks would still be moving when the spring is maximally compressed, so we would have needed to determine their speeds to determine the total mechanical energy when the spring is compressed.
When we calculated the initial kinetic energy, we found that it was given by:
\[\begin{aligned} E=\frac{1}{2} \left(\frac{mM}{m+M}\right)(v_M-v_m)^2 &=\frac{1}{2}M_{red}(v_M-v_m)^2\end{aligned}\]
The combination of masses in parentheses is called the “reduced mass” of the system, and is a sort of effective mass that can be used to model the system as a whole.
A uniform wire is bent into a semi-circle of radius \(R\). Where is the center of mass of the wire?
- Answer
-
The curved wire is illustrated in Figure \(\PageIndex{3}\), along with a small mass element, \(dm\), on the wire, and our choice of coordinate system (centered at the center of the semi-circle). By symmetry, the position of the center of mass will be located at \(x=0\), so we only need to determine the \(y\) position.
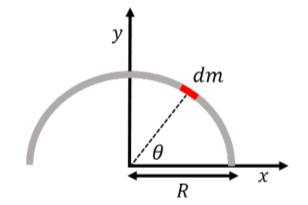
Figure \(\PageIndex{3}\): A uniform wire bent into a semi circle of radius \(R\), and a small mass element, \(dm\), on the wire. The \(y\) position of the center of mass is given by:
\[\begin{aligned} y_{CM} = \frac{1}{M}\int y dm\end{aligned}\]
where \(M\) is the total mass of the wire. We can define the mass per unit length, \(\lambda\), for the wire as:
\[\begin{aligned} \lambda =\frac{M}{\pi R}\end{aligned}\]
We will choose to integrate the equation for the \(y\) position of the center of mass over \(\theta\) (from 0 to \(\pi\)), instead of over \(y\), as it will make the integral easier (it is easier to express \(dm\) in terms of \(d\theta\) than \(dy\) because the wire is curved). \(\theta\) is the angle at which the mass element is located. The mass element forms an arc on the wire of length \(ds\) that subtends an angle \(d\theta\). The two are related by:
\[\begin{aligned} ds = Rd\theta\end{aligned}\]
The mass element, \(dm\), can then be expressed in terms of the mass per unit length of the wire and the length, \(Rd\theta\), of the mass element:
\[\begin{aligned} dm = \lambda ds = \lambda Rd\theta\end{aligned}\]
We also need to express the \(y\) position of the mass element using \(\theta\):
\[\begin{aligned} y = R\sin\theta\end{aligned}\]
Now that we have expressed \(dm\) and \(y\) in terms of \(\theta\), we can determine the \(y\) position of the center of mass:
\[\begin{aligned} y_{CM} &= \frac{1}{M}\int y dm = \frac{1}{M}\int_0^\pi R\sin\theta \lambda Rd\theta\\[4pt] &= \frac{R^2\lambda}{M}\int_0^\pi \sin\theta d\theta = \frac{R^2\lambda}{M} \bigl[-\cos\theta\bigr]_0^\pi\\[4pt] &=\frac{2R^2\lambda}{M}=\frac{2R}{\pi}\end{aligned}\]
where in the last equality, we used the expression for the mass per unit length, \(\lambda\), obtained above.