11.1: Rotational kinematic vectors
( \newcommand{\kernel}{\mathrm{null}\,}\)
Before proceeding, you may wish to review:
- Section 4.4 on kinematics for circular motion.
- Section A1.3 on the vector product.
- Section A1.4 on axial vectors and their use in defining rotational quantities.
Scalar rotational kinematic quantities
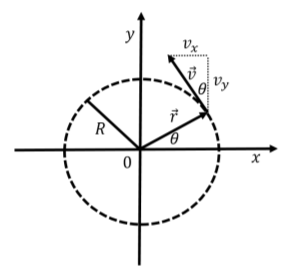
Recall that we can describe the motion of a particle along a circle of radius, R, by using its angular position, θ, its angular velocity, ω, and its angular acceleration, α. With a suitable choice of coordinate system, the angular position can be defined as the angle made by the position vector of the particles, →r, and the x axis of a coordinate system whose origin is the center of the circle, as shown in Figure 11.1.1.
The angular velocity, ω, is the rate of the change of the angular position, and the angular acceleration, α, is the rate of change of the angular velocity:
ω=ddtθα=ddtω
If the angular acceleration is constant, then angular velocity and position as a function of time are given by:
ω(t)=ω0+αtθ(t)=θ0+ω0t+12αt2
where θ0 and ω0 are the angular position and velocity, respectively, at t=0.
We can also describe the motion of the particle in terms of “linear” quantities (as opposed to “angular” quantities) along a one-dimensional axis that is curved along the circle. If s is the distance along the circumference of the circle, measured counter-clockwise from where the circle intersects the x axis, then it is related to the angular displacement:
s=Rθ
if θ is expressed in radians. Similarly, the linear velocity along the s axis, vs, and the corresponding acceleration, as, are given by:
vs=dsdt=ddtRθ=Rωas=dvdt=ddtRω=Rα
where the radius of the circle, R, is a constant that can be taken out of the time derivatives. For motion along a circle, the velocity vector, →v, of the particle is always tangent to the circle (Figure 11.1.1), so vs corresponds to the speed of the particle. The acceleration vector, →a, is in general not tangent to the circle; as represents the component of the acceleration vector that is tangent to the circle. If as=0, then α=0, and the particle is moving with a constant speed (uniform circular motion), and the acceleration vector points towards the center of the circle.
Which of the following statements correctly describes the speeds at points A and B on the disk rotating about an axis through its center, as illustrated in Figure 11.1.2?
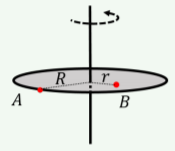
- Both points A and B have the same angular and linear speeds.
- Both points A and B have the same linear speed but they have different angular speeds.
- Both points A and B have the same angular speed but they have different linear speeds.
- Answer
- C.
Vector rotational kinematic quantities
In the previous section, we defined angular quantities to describe the motion of a particle about the z axis along a circle of radius R that lies in the xy plane. By using vectors, we can define the angular quantities for rotation about an axis that can point in any direction. Given an axis of rotation, the path of any particle rotating about that axis can be described by a circle that lies in the plane perpendicular to that axis of rotation, as illustrated in Figure 11.1.3.
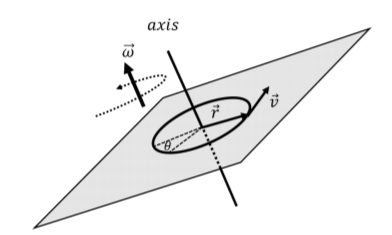
We define the vector, →r, for a particle to be the vector that goes from the axis of rotation to the particle and is in a plane perpendicular to the axis of rotation, as in Figure 11.1.3. Given the velocity vector of the particle, →v, we define its angular velocity vector, →ω, about the axis of rotation, as:
→w=1r2→r×→v
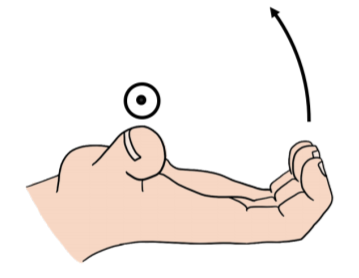
The angular velocity vector is perpendicular to both the velocity vector and the vector →r, since it is defined as their cross-product. Thus, the angular velocity vector is co-linear with the axis of rotation. By using the angular velocity vector, we can specify the direction of the axis of rotation as well as the direction in which the particle is rotating about that axis. The direction of rotation is given by the right hand rule for axial vectors: when you point your thumb in the same direction as the angular velocity vector, the direction of rotation is the direction that your fingers point when you curl them, as illustrated in Figure 11.1.4.
This definition of the angular velocity is consistent with the description from the previous section for motion about a circle of radius R that lies in the xy plane, as in Figure 11.1.1. In that case, the magnitude of the angular velocity is given by:
ω=1r2||→r×→v||=1r2rvsinϕ=vR∴v=Rω
where ϕ is the angle between the vectors →r and →v (90∘ for motion around a circle). The direction of the angular velocity in Figure 11.1.1 is in the positive z direction, which corresponds to counter-clockwise rotation about the z axis.
You push on the right-hand side of a door to open it, as the door’s hinges are on the left. The angular velocity vector of the door is:
- Upwards
- Downwards
- Forwards
- Backwards
- Answer
- A.
One can always define an angular velocity vector relative to a point of rotation, even if the particle is not moving along a circle. If we define the vector →r to be the vector from the point of rotation to the particle, then the angular velocity vector describes the motion of the particle as if it were instantaneously moving in a circle centered at the point of rotation, in a plane given by the vectors →r and →v.
Consider, for example, the particle in Figure 11.1.5 which is moving in a straight line with a velocity vector in the xy plane at a position →r relative to the origin. We can define its angular velocity vector relative to the origin, which will be in the positive z direction.
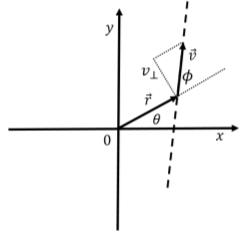
The angular velocity describes the motion of the particle as if it were instantaneously moving along a circle of radius r centered about the origin. The angular velocity is related to the component of →v, v⊥, that is perpendicular to →r (which is the component tangent to the circle of radius r, in Figure 11.1.5):
||→w||=1r2||→r×→v||=vsinφr=v⊥r
where ϕ is the angle between →r and →v.
Similarly, we can define the angular acceleration vector, →α, about an axis of rotation:
→α=1r2→r×→a
where →a is the particle’s acceleration vector, and →r is the vector from the axis of rotation to the particle. The direction of the angular acceleration is co-linear with the axis of rotation and the right-hand rule gives the rotational direction of the angular acceleration. We can also define the angular acceleration about a point; in that case, the direction of the vector will define an instantaneous axis of rotation about a circle of radius r centered at the point as well as the direction of the angular acceleration about that axis.
Finally, we can define an angular displacement vector, →θ, relative to an axis of rotation. The direction of the angular displacement vector will be co-linear with the axis of rotation, its direction will indicate the direction of rotation about that axis, and its magnitude (in radians) will correspond to the angular displacement (as shown in Figure 11.1.3). We can only relate the angular displacement vector to an infinitesimal linear displacement vector, d→s, since the position vector →r from the axis of rotation will be different at each end of the displacement vector if the displacement is large. The infinitesimal angular displacement vector that corresponds to an infinitesimal displacement vector, d→s, is defined as:
d→θ=1r2→r×d→s
Which statement is correct regarding an ant on a disk that is rotating slower and slower as illustrated?
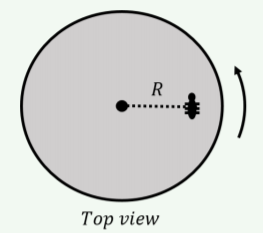
- The angular velocity points into the page and the angular acceleration points out of the page.
- Both the angular velocity and acceleration point into the page.
- Both the angular velocity and acceleration point out of the page.
- The angular acceleration points into the page and the angular velocity points out of the page.
- Answer
- D.
The instantaneous angular velocity vector is the rate of change of the angular displacement vector:
→ω=d→θdt=ddt1r2→r×d→s=1r2→r×→vs
where →vs is the (instantaneous) tangential velocity around the circle (i.e. the component of the velocity →v that is perpendicular to →r). The angular acceleration vector is the rate of change of the angular velocity vector:
→α=ddt→ω
Given the angular kinematic quantities, the related linear quantities at a position →r from the axis of rotation are given by:
d→s=d→θ×→r
→vs=→w×→r
→as=→α×→r
where the linear quantities are always in the direction perpendicular to →r (tangent to the circle, for motion around a circle). In other words, one cannot, say, take the acceleration vector, obtain the angular acceleration vector, and then get back the original acceleration vector - one will only get back the component of the acceleration vector that is perpendicular to →r.
A particle has an angular velocity in the negative z direction. In which way is the particle’s velocity vector at a point in its trajectory when it is on the positive y axis?
- Positive z direction
- Negative y direction
- Positive x direction
- Negative x direction
- Answer
- C.

