15.6: Sample problems and solutions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A man and a woman, Rebecca (57 kg) and Ryan (63 kg), are on a cruise when their ship tragically sinks. They are thrust into the freezing cold ocean. They see a large wooden door floating on the surface of the water, and wonder if they could both survive if they both lay on top of the door. They estimate that the door measures about 2 m×1 m×0.12 m. The density of salt water is ρ_{w} = 1027 \text{kg/m}^{3}.

- What does the density of the wood have to be in order for Rebecca and Ryan to stay above the surface of the water? (see Figure \PageIndex{1})
- If the door is made of oak (ρ_{d} = 750\text{ kg/m}^{3}), will they survive? Can one of them survive?
- Answer
-
a. The forces acting on the door are the force of buoyancy, the door’s weight, and the weights of Rebecca and Ryan, as shown in Figure \PageIndex{2}.
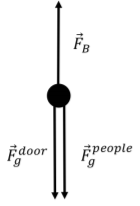
Figure \PageIndex{2}: The forces acting on the door when Rebecca and Ryan are on top of it. We can combine the weight of the door and the weight of the people into the total weight, F_{g}. We choose the y axis to be positive upwards. The sum of the forces on the door in the y direction is given by:
\begin{aligned}\sum F_{y}=F_{B}-F_{g} \end{aligned}
For the door to float, the net force on the door must be greater than or equal to zero. We want to find the minimum buoyant force for them to float, so we set the net force equal to zero:
\begin{aligned} F_{g}&=F_{B} \\[4pt] (m_{R}+m_{r}+m_{d})g&=\rho_{w}V_{w}g \\[4pt] m_{R}+m_{r}+m_{d}&=\rho_{w}V_{w} \end{aligned}
where the weight includes the mass of Rebecca (m_{R}), Ryan (m_{r}) and the door (m_{d}). We added the subscript W to the right side of the equation to remind ourselves that the buoyant force depends on the density and volume of the displaced water. We want to find the maximum density of the wood in order for Rebecca and Ryan to stay above the water’s surface. This means that the maximum volume of water that can be displaced is the volume of the door, V_{w} = V_{d} (so that the surface of the door is level with the surface of the water, as in Figure \PageIndex{1}). We can rewrite the mass of the door in terms of its volume and density, and apply our condition that V_{w} = V_{d}:
\begin{aligned} m_{R}+m_{r}+\rho_{d}V_{d}&=\rho_{w}V_{d} \\[4pt] \rho_{d}&=\frac{\rho_{w}V_{d}-m_{R}-m_{r}}{V_{d}} \end{aligned}
A quick calculation tells us that the volume of the door is (2\text{ m})(1\text{ m})(0.12\text{ m}) = 0.24\text{ m}^{3}. We can now calculate the desired density of the wood:
\begin{aligned} \rho_{d}&=\frac{\rho_{w}V_{d}-m_{R}-m_{r}}{V_{d}} \\[4pt] \rho_{d}&=\frac{(1027\text{kg/m}^{3})(0.24\text{m}^{3})-57\text{kg}-63\text{kg}}{0.24\text{m}^{3}} \\[4pt] \rho_{d}&=527\text{kg/m}^{3} \end{aligned}
The maximum density of the wood that would allow them to both float is 527\text{ kg/m}^{3}. Balsa wood has a density that is about 150\text{ kg/m}^{3}, so would allow them to survive. However, it is unlikely that a random floating door is made of balsa wood (although one would choose lighter materials when constructing a ship).
b. No, they could not both stay on the door because the density of oak is greater than the maximum density of 527\text{ kg/m}^{3}. We can find the amount of mass that can be added to the door (m_{A}) in order for the person on it to stay above water:
\begin{aligned} F_{g}&=F_{B} \\[4pt] (m_{A}+m_{d})g&=\rho_{w}V_{w}g \\[4pt] m_{A}+\rho_{d}V_{d}&=\rho_{w}V_{w} \\[4pt] m_{A}+\rho_{d}V_{d}&=\rho_{w}V_{d} \\[4pt] m_{A}&=V_{d}(\rho_{w}-\rho_{d}) \end{aligned}
where we again used the condition that V_{w} = V_{d}. We can plug in the appropriate values and solve:
\begin{aligned} m_{A}&=V_{d}(\rho_{w}-\rho_{d}) \\[4pt] m_{A}&=(0.24\text{m}^{3})(1027\text{kg/m}^{3}-750\text{kg/m}^{3}) \\[4pt] m_{A}&=66\text{kg} \end{aligned}
The door can support an additional mass of 66\text{ kg}, so either Rebecca or Ryan can survive if the other does not get on the door.
A doctor prescribes an IV drip to a dehydrated patient. She asks a nurse, Rob, to administer 2\text{ l} of saline solution (η = 1.0 × 10^{−3}\text{ Pas}, ρ = 997\text{ kg/m}^{3}) to the patient over 2 hours. An IV drip works by inserting a needle into a vein in a patient’s arm. The needle is connected to an IV bag by a tube (Figure \PageIndex{3}). Lily uses a needle that has a diameter of 0.60\text{ mm} and a length of 32\text{ mm}. The blood pressure in the patient’s veins is 80\text{ mmHg} above atmospheric pressure. Note: 1\text{ mmHg} ≈ 133\text{ Pa}.
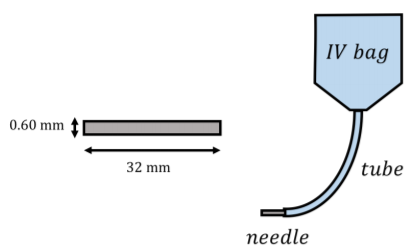
- What must the pressure be at the entrance of the needle (the side connected to the saline, not the patient)? Assume that the needle is essentially horizontal and that the diameter of the tube from the IV bag is large enough so that resistance in the vertical tube is negligible. Write your answer in Pascals above atmospheric pressure.
- How high above the patient’s arm should Lily put the IV bag?
- Answer
-
a. Given that the pressure in the patient’s veins is 80\text{ mmHg} above atmospheric pressure, we want to find the pressure required at the other end of the needle so that we get the desired flow rate through the needle. We model the needle as a horizontal cylindrical pipe and assume that the saline solution exhibits laminar flow. We can therefore use Poiseuille’s equation:
\begin{aligned} Q=\frac{\pi r^{4}}{8ηL}(P_{1}-P_{2})\end{aligned}
We let P_{1} be the pressure where the needle connects to the tube. Solving for P_{1} gives:
\begin{aligned} P_{1}=Q\frac{8ηL}{\pi r^{4}}+P_{2}\end{aligned}
The pressure at the exit of the needle, P_{2}, is just the blood pressure (80\text{ mmHg}+1\text{atm}). The radius of the needle is 0.60\text{ mm/}2 = 0.30\text{ mm}. The flow rate has to be in units of \text{m}^{3}\text{/s}. The flow rate in the appropriate units is thus:
\begin{aligned} Q=\frac{21}{2\text{ hr}}\cdot\frac{1\text{ hr}}{3600\text{ s}}\cdot \frac{0.001\text{ m}^{3}}{11} =2.8\times 10^{-7}\text{m}^{3}\text{/s} \end{aligned}
Using our values, we can calculate P_{1}:
\begin{aligned} P_{1}&=(2.8\times 10^{-7}\text{m}^{3}\text{/s})\frac{8(1.0\times 10^{-3}\text{Pas})(0.032\text{m})}{\pi(3\times 10^{-4}\text{m})^{4}}+80\text{mmHg}\cdot\frac{133\text{Pa}}{1\text{mmHg}}+1\text{atm} \\[4pt] P_{1}&=2817\text{Pa}+10640\text{Pa}+1\text{atm} \\[4pt] \therefore P_{2}&=13457\text{Pa}\quad\text{above atmospheric pressure} \end{aligned}
b. We can easily determine the height of the IV bag that is required to give the desired pressure. We choose a coordinate system with a y axis that is vertical (positive upwards) with the origin at the location of the needle (Figure \PageIndex{4}).
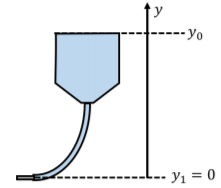
Figure \PageIndex{4}: The needle is at height 0 and the top of the fluid in the IV bag is at y_{0}. At the top of the solution in the IV bag, y_{0}, the solution has a speed of zero and is at atmospheric pressure, P_{0} = 1\text{ atm}. The velocity at the needle is 0, and the pressure is 13457\text{ Pa} + 1\text{ atm}. Bernoulli’s principle states:
\begin{aligned} P_{0}+\frac{1}{2}\rho v_{0}^{2}+\rho gy_{0}=P_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gy_{1} \end{aligned}
Using our values to solve for y_{0}, we get:
\begin{aligned} P_{0}+\rho gy_{0}&=P_{1} \\[4pt] y_{0}&=\frac{P_{1}-P_{0}}{\rho g} \\[4pt] y_{0}&=\frac{13457\text{ Pa}+1\text{ atm}-1\text{ atm}}{(997\text{kg/m}^{3})(9.8\text{m/s}^{2})} \\[4pt] y_{0}&= \frac{13457\text{ Pa}}{(997\text{ kg/m}^{3})(9.8\text{ m/s}^{2})} \\[4pt] y_{0}&=1.4\text{ m} \end{aligned}
Therefore, the IV bag should be placed 1.4\text{ m} above the patient’s arm.

