16.7: Sample problems and solutions

Exercise \(\PageIndex{1}\)

Consider three charged rods of length \(L\) which are arranged to form a triangle, as shown in Figure \(\PageIndex{1}\). If the charge on each rod is evenly distributed, what is the net electric field at the center of the triangle?

Figure \(\PageIndex{1}\): A triangle made up of charged rods.

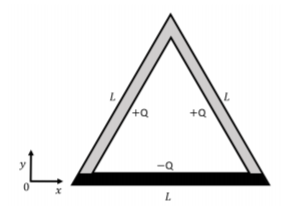
Answer

We can model the object as the sum of three finite length wires of the length, \(L\). In Example 16.3.3, we determined that the electric field produced by a finite wire is: \[\begin{aligned} E = \frac{2k\lambda}{R}\sin\theta_0\end{aligned}\] We can determine geometrically that \(\theta_0 = \frac{\pi}{6}\), as in Figure \(\PageIndex{2}\). The distance, \(R\): \[\begin{aligned} R = \frac{L}{2}\sin{\theta_0}\end{aligned}\]

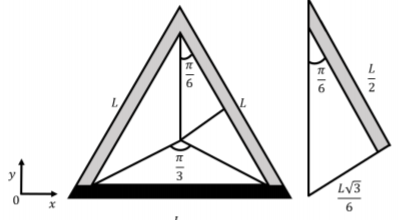
Figure \(\PageIndex{2}\)

Thus, the field from one wire is given by: \[\begin{aligned} E&= \frac{2k\lambda}{R}\sin(\frac{\pi}{6})\\ E &= \frac{k\lambda}{R}\end{aligned}\] Given that the charge \(Q\) is evenly distributed along the rod of length \(L\), we can rewrite the charge density as \(\frac{Q}{L}\), which gives: \[\begin{aligned} E &= \frac{k Q}{RL} = \frac{k Q}{\frac{L\sqrt{3}}{6}L} = \frac{6k Q}{\sqrt{3}L^2}\end{aligned}\] This is the magnitude of the electric field for each side of the triangle. The two positive wires will produce electric fields whose vertical components cancel. The negative wire will produce a field that points downwards. Summing together the electric field vectors: \[\begin{aligned} \sum \vec E &= \frac{6k Q}{\sqrt{3}L^2}\left(\cos\left({\frac{\pi}{6}}\right) - \cos\left({\frac{\pi}{6}}\right)\right)\hat{x} + \frac{6k Q}{\sqrt{3}L^2}\left(-1-2\sin\left({\frac{\pi}{6}}\right)\right)\hat y\\ \sum \vec E & = -\frac{12k Q}{\sqrt{3}L^2}\hat y\end{aligned}\] Which is the final answer.

Exercise \(\PageIndex{2}\)

Suppose a dipole is in an electric field \(\vec E\). Show that the dipole will experience simple harmonic motion if the angle between the dipole vector and the electric field vector is small.

Answer

The only net torque on the dipole is from the force from the electric field: \[\begin{aligned} \tau = -pE\sin\theta \end{aligned}\] where we have inserted a minus sign to indicate that this is a restoring torque, in the opposite direction of increasing angle \(\theta\). The net torque is equal to the moment of inertia times the angular acceleration: \[\begin{aligned} -pE\sin\theta &= I\alpha\\ \therefore \alpha &= -\frac{pE}{I}\sin\theta\sim-\frac{pE}{I}\theta\end{aligned}\] where in the last equality, we made the small angle approximation (\(\sin\theta\sim\theta\)). This has the form for simple harmonic motion: \[\begin{aligned} \frac{d^2\theta}{dt^2}&=-\omega^2 \theta\\ \omega &=\sqrt{\frac{pE}{I}}\end{aligned}\]