18.1: Electric Potential Energy
- Page ID
- 19495
- Section 8.1 on conservative forces.
- Section 9.3 on the derivation of gravitational potential energy.
Mathematically, Coulomb’s Law for the electric force is identical to Newton’s Universal Theory of Gravity for the gravitational force. The electric force is thus conservative, and the work done by the electric force on a charge, \(q\), when the charge moves from position, \(A\), in space to some other position, \(B\), cannot depend on the path taken. Since the work done by the electric force only depends on the location of the initial (\(A\)) and final (\(B\)) positions, we can define an electrical potential energy function, \(U(\vec r)\), that depends on position, \(\vec r\). The work done by the electric force, \(\vec F^E\), on a charge in going from position, \(A\) (defined by position vector, \(\vec r_A\)), to position, \(B\) (defined by position vector, \(\vec r_B\)), can be written as:
\[W=\int_A^B \vec F^{E}\cdot d\vec r=-\Delta U=-[U(\vec r_{B})-U(\vec r_{A})]\]
In order to determine the function, \(U(\vec r)\), we can choose a path over which the integral for work is easy to calculate. Consider the work done by the electric force from a point charge, \(+Q\), exerted on a charge, \(+q\), when \(+q\) moves from a distance \(r_A\) to a distance \(r_B\) from the center of \(+Q\), as illustrated in Figure \(\PageIndex{1}\).
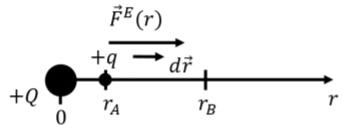
Placing \(+Q\) at the origin of a coordinate system, the force exerted on charge, \(+q\), when it is located at position, \(\vec r\), is given by:
\[\begin{aligned} \vec F^E=k\frac{Qq}{r^2}\hat r\end{aligned}\]
The work done by the electric force when \(+q\) moves from \(A\) to \(B\) is given by:
\[\begin{aligned} W&=\int_A^B \vec F^E\cdot d\vec r=\int_{\vec r_A}^{\vec r_B} \left(k\frac{Qq}{r^2}\hat r\right)\cdot d\vec r=kQq \int_{r_A}^{r_B} \frac{1}{r^2}dr\\[4pt] &=kQq \left[\frac{-1}{r} \right]_{r_A}^{r_B}=-\left(\frac{kQq}{r_B}-\frac{kQq}{r_A}\right)\end{aligned}\]
where we noted that since \(\vec F^E\) and \(d\vec r\) are parallel, their scalar product is simply the product of their magnitudes. By comparing with Equation 18.1.1, we can identify the potential energy, \(U(\vec r)\), of a charge, \(+q\), located at a relative position, \(\vec r\), from a point charge, \(+Q\), as:
\[U(\vec r)=\frac{kQq}{r}+C\]
where the potential energy is only defined up to some constant, \(C\), which cancels when we take the difference in potential energy between two positions. Note that this is very similar to the function for the gravitational potential energy of a mass, \(m\), a distance, \(r\), from a mass, \(M\) (see Section 9.3).
The potential energy function that we derived above remains the same if one or both of the charges change sign, as the derivation did not depend on the sign of the charges, \(q\) and \(Q\), as changing the sign of one charge changes the direction of the force. For example, a positive charge, \(+q\), near a negative charge, \(-Q\), would have negative electric potential energy with the choice \(C=0\), in exact analogy with gravity.
Electrostatic potential energy
When we hold two positive charges together a distance, \(r\), apart, we need to exert a force on the charges in order to keep the charges in place (as they repel each other). If we release the charges, they will move apart from each other, and eventually all of the stored electric potential energy is converted into kinetic energy. The energy that was originally stored in this “system” of two charges is called “electrostatic potential energy”. In this section, we show how to model the energy stored in a collection of point charges.
Consider a single positive charge, \(q_1\), located at the origin of empty space. Since there are no other charges present, it does not “cost” us any energy to place that charge there - we do not need to do any work. If we now bring in a second positive charge, \(q_2\), and place it a distance, \(r_{12}\), from \(q_1\) (Figure \(\PageIndex{2}\)), we will need to do work since \(q_1\) exerts a force on \(q_2\). If we define zero potential energy to be at infinity (choosing \(C=0\) for electric potential energy), the work, \(W_{q2}\), that we must do on \(q_2\) to bring it from infinity to a distance, \(r_{12}\), from \(q_1\) is given by the corresponding change in potential energy of \(q_2\):
\[\begin{aligned} W_{q2}=\Delta U=U_{final}-U_{initial}=k\frac{q_1q_2}{r_{12}}-0=k\frac{q_1q_2}{r_{12}}\end{aligned}\]
Note that the work is done by us (not by the electric field), so it has the same sign as the change in potential energy (we must do positive work to increase potential energy). The work that we did corresponds to the same amount of electrostatic potential energy stored in this arrangement of two charges (the only source of that stored electrostatic potential energy is the work that we did on the charge \(q_2\)).
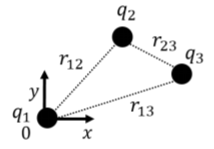
Now, we bring in a third positive charge, \(q_3\), also from infinitely far away, as illustrated in Figure \(\PageIndex{2}\). In order to bring in \(q_3\), we need to do work against the forces exerted by both \(q_1\) and \(q_2\). Suppose that we place \(q_3\) a distance \(r_{13}\) from \(q_1\) and \(r_{23}\) from \(q_2\). Then, the amount of work done by us to bring in \(q_3\) is given by:
\[\begin{aligned} W_{q3}=k\frac{q_1q_3}{r_{13}}+k\frac{q_2q_3}{r_{23}}\end{aligned}\]
and the total electrostatic energy stored in the system of three charges is given by the sum of the work done to place \(q_2\) and the work done to place \(q_1\):
\[\begin{aligned} E = W_{q1}+W_{q2}+W_{q3}=0+k\frac{q_1q_2}{r_{12}}+k\frac{q_1q_3}{r_{13}}+k\frac{q_2q_3}{r_{23}}\end{aligned}\]
If we have any number of charges (positive and negative), we can always calculate the stored electrostatic energy by proceeding in a similar fashion.
Four charges of varying magnitude are fixed in position. If the electric potential energy stored in the system were to be calculated as above, how many terms would be in the sum?
- Four.
- Two.
- One.
- Six.
- Answer
-