23.9: Sample problems and solutions
- Page ID
- 19549
Exercise \(\PageIndex{1}\)
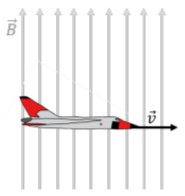
In the 1950s, the Royal Canadian Air Force developed a jet airplane called the Avro Arrow. This jet reached a speed of mach 1.9 (\(652\text{ms}^{-1}\)), and was considered one of the most advanced airplanes that existed at the time. Suppose that the Avro Arrow is traveling at a velocity of \(v = 652\text{ms}^{-1}\) above the Sout Pole through Earth’s vertical magnetic field, \(B = 5.2\times 10^{-5}\text{T}\), as shown in Figure \(\PageIndex{1}\). If the Avro Arrow had a wingspan of \(l = 15\text{m}\), determine the induced voltage across its wings.
- Answer
-
This is identical to the motional emf that is generated by a bar moving in a magnetic field. As the airplane moves as illustrated (towards the left, in an upwards magnetic field), the electrons in the wing of the airplane will be pushed into the page. Eventually, the electric field from the electrons will prevent further electrons from accumulating at that side of the wing, and there will be a constant (Hall) voltage, \(\Delta V\), across the wing tips. This will happen when the magnetic and electric force are equal and opposite: \[\begin{aligned} qvB &= qE = q\frac{\Delta V}{L}\end{aligned}\] where \(L\) is the wingspan of the airplane. The induced potential is thus given by: \[\begin{aligned} \Delta V = BLv = (5.2\times 10^{-5}\text{T})(15\text{m})(652\text{ms}^{-1})=0.51\text{V}\end{aligned}\]
Exercise \(\PageIndex{2}\)
A generator is made of \(N\) circular loops of radius, \(R=0.3\text{m}\), rotating at a frequency of \(f=60\text{Hz}\), in a uniform magnetic field, \(B=0.1\text{T}\). How many coils must the generator have in order for it to produce an alternating voltage with a maximum amplitude of \(\Delta V =110\text{V}\).
- Answer
-
The voltage produced by a generator is given by: \[\begin{aligned} \Delta V&=NAB\omega\sin(\omega t)\end{aligned}\] and the angular frequency is given by \(\omega = 2\pi f\). The number of required coils is thus: \[\begin{aligned} N=\frac{\Delta V}{AB\omega}=\frac{\Delta V}{\pi R^2B2\pi f}=\frac{(110\text{V})}{2\pi^2(0.3\text{m})^2(0.1\text{T})(60\text{Hz})}=10.3\end{aligned}\] Thus, one requires 10 loops in the coil to generate the desired voltage.