24.3: Time Dilation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Einstein was famous for his “thought experiments”, which allow us to understand the consequences of a theory by performing thought experiments that would be impractical to actually carry out (such as the experiment with Alice and Brice described above, which would be impractical to carry out, since the speed of light is so high that Brice would never notice that clock A emitted the pulse slightly earlier).
Imagine that we build a clock using a pulse of light traveling (oscillating) back and forth between two mirrors, separated by a distance, L, as illustrated in Figure 24.3.1.
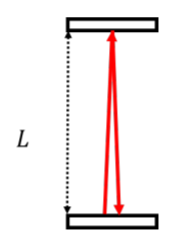
Since the speed of light is, c, the time that it will take for the pulse of light to travel back and forth between the two mirrors, namely the period of the clock, is given by:
Δt=2Lc
where the speed of light, c, is given by the total distance traveled by the pulse of light divided by the time taken to do so:
c=2LΔt
Now, imagine placing this clock on a spaceship that travels with speed, v, perpendicular to the direction of the movement of the light. The clock is illustrated in Figure 24.3.2, as seen from the ground.
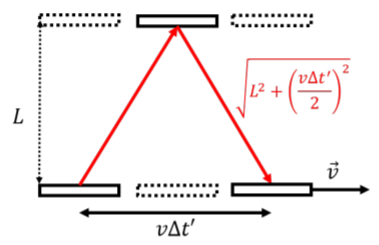
From the perspective of a person watching the clock go by, the pulse of light travels a larger distance over one clock period, since the mirrors move to the right as the pulse of light moves up and down. However, by Einstein’s second postulate, the pulse of light must still travel with the same speed, c, so it must take the pulse of light longer to bounce between the two mirrors than it did when the clock is at rest. Let us determine the relationship between the period of the clock, Δt, measured when the clock is at rest, and the period of the clock, Δt′, as measured by an observer that sees the clock go by with speed, v.
To an observer that sees the clock move by with speed, v, the speed of the pulse of light, which must also be equal to c, is given by:
c=2√L2+(vΔt′2)2Δt′
where the distance in the numerator was simply found by Pythagoras’ theorem, as the spaceship will travel a horizontal distance, vΔt′, as measured by the observer that is not moving with the spaceship. Squaring this relationship, we can isolate the period of the clock, Δt′, as measured by the observer that sees the clock move with speed, v:
c2=4L2Δt′2+v2Δt′2(c2−v2)=4L2∴Δt′=2L1√c2−v2=2Lc1√1−v2c2
Note that the term, 2L/c, is simply the period of the clock as measured in a frame of reference where the clock is stationary. Thus, we can relate the two clock periods:
Δt′=Δt1√1−v2c2
To re-iterate: the period of the clock, Δt′, as measured in a frame of reference that is moving relative to the clock is longer than the period of the clock, Δt, as measured in the “rest frame” of the clock (the reference frame where the clock is stationary). We call this effect “time dilation”, and it is not just some mathematical curiosity. The clock that we imagined with a pulse of light is a real clock that one could actually construct; we could use it to measure time. That clock will appear to tick slower if it is moving. Time goes by slower in a moving reference frame. If a person climbs on a ship that is moving, that person will age at a slower rate than a person that remained on Earth. By traveling at high speeds, you effectively travel into the future, as observed on Earth. The equation above allows us to relate the amount of time that went by in one reference frame to the amount of time that went by in a different frame of reference.
We define the time that is measured at rest as the “proper time”. In our example, Δt, is the proper time (proper period) for the clock, since it is defined in a frame of reference where the clock is at rest. The “dilated time”, Δt′, is measured in a frame of reference that is moving relative to the clock.
The factor by which time is dilated comes up often in Special Relativity, and is called the gamma factor:
γ=1√1−v2c2
As a corollary to Einstein’s postulates, we will see that nothing can ever exceed the speed of light in vacuum. The gamma factor is always greater than 1, since v (the speed between the two different inertial frames of reference), must always be smaller than c. You may also recognize that the gamma factor appeared in our introductory example with the force between two wires. Here, we derived the gamma factor from kinematical considerations, whereas in the example with the two wires, it came straight out of the equations for electromagnetism.
What is gamma for a speed of v=0.75c?
- 1.51
- 0.75
- 75
- 1.68
- Answer
-
A.
What speed corresponds, v, to a gamma factor of 2.5?
- v=2.5c
- v=0.92c
- v=0.25c
- v=0.47c
- Answer
-
B.
Time-dilation is a real effect that has been observed, for example by placing high precision atomic clocks on an airplane to observe their period slow down. Another example of time-dilation is the fact that we observe many particles called muons at the surface of the Earth. Muons are very similar to electrons, except that they have a larger mass, and that they are unstable (they radioactively decay into an electron and neutrinos, after 2.2μs on average). Muons are produced in large amounts when cosmic rays (high energy particles from outside our Solar System) strike the molecules in our upper atmosphere, at altitudes of tens of kilometers. As the muons travel down towards the Earth, they decay.
Suppose that muons are produced traveling at the speed of light; in that case, they would travel a distance d=(3×108m/s)(2.2×10−6s)=(660m), on average, before decaying. However, muons are produced tens of kilometers above the surface of the Earth, travel slower than the speed of light, and yet, we are able to detect many muons at the surface of the Earth. We would expect that all muons would have decayed before reaching the surface of the Earth.
We can understand this in terms of time dilation; in the reference frame of the muon, the muon decays after Δt=2.2μs. In a reference frame from which the muon appears to move with speed, v, the “clock” that measures how long the muon has existed ticks slower. Thus, from the Earth, we observe that the muon takes longer than 2.2μs to decay, giving it time to reach the surface of the Earth.
A muon travels with a speed of 0.9c as observed from the surface of the Earth. As measured in the frame of reference of the Earth, how far has the muon traveled after 2.2μs have elapsed in the muon’s frame of reference?
Solution
The muon is traveling with a speed of v=0.9c relative to the Earth, thus the gamma factor is given by:
γ=1√1−v2c2=1√1−0.92=2.29
The amount of time that goes by in the frame of reference of the Earth, Δt, when Δt′=2.2μs has gone by in the muon’s frame of reference will be dilated by the gamma factor. Δt′ is the proper time in the muon frame’s of reference, which corresponds to a longer time in Earth’s frame of reference:
Δt=γΔt′=(2.29)(2.2μs)=5.0μs
In the frame of reference of the Earth, the muon has traveled a distance:
d′=vΔt′=(0.9c)(5.0μs)=1350m
Discussion
In this example, we see that an object, such as a muon, that travels with a speed that is 90 percent of the speed of light will have a gamma factor around 2. Thus, from the Earth’s frame of reference, it appears that the muons “ages” at about half of the rate at which one would observe the muon to age if moving along with the muon. This is the mechanism that allows muons to exist much longer than 2.2\mus when they are traveling relative to the Earth.
Also, in Earth’s reference frame, the muons travel a distance of 1350m in the period of time between being produced and decaying. In the reference frame of the muon, only 2.2μs elapse as the Earth moves closer to the muon, at the same speed. In the reference frame of the muon, the Earth has traveled a distance:
d′=vΔt=(0.9c)(2.2μs)=594m
Thus, as viewed from the muon’s frame of reference, the distance that it traveled between being produced and decaying is about half the distance as measured in the Earth’s reference frame. This is called “length contraction” and is a necessary consequence of time-dilation.
A spaceship carrying your friend Alice speeds away at a speed of 0.99c towards the nearest star, Proxima Centauri, a distance of 4.2ly (light-years) away. How much time does the trip take as measured by Alice?
Solution
How far has the spaceship traveled, according to Alice? Alice’s trip is illustrated in Figure 24.3.3, showing the trip as viewed from Earth’s and from Alice’s frame of reference.
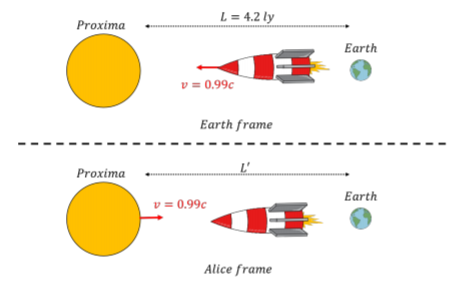
In Earth’s frame of reference, the spaceship travels a distance of 4.2ly at a speed of 0.99c, which will take a time, Δt′, given by:
Δt′=(4.21ly)(0.99c)=4.2y
which is not surprising, since Alice is traveling at almost the speed of light. This is the time that goes by on planet Earth. Since Alice’s spaceship is moving, less time will go by on the spaceship, as the 4.2y is the dilated time measured at Earth, not the proper time measured by Alice. First, we determine the gamma factor:
γ=1√1−v2c2=1√1−0.992=7.1
The proper time measured by Alice is:
Δt=Δt′γ=(4.2y)(7.1)=0.6y
That is, Alice only ages by 0.6y (about 7 months), while everyone on Earth ages by 4.2y!
In Alice’s frame of reference, she is not moving, and Proxima Centauri moves towards her at a speed of 0.99c. Since her trip only lasts about 7 months (0.6y), Proxima Centauri moves towards her by a distance, L′:
L′=(v)(Δt)=(0.99c)(0.6y)=0.6ly
as illustrated in Figure 24.3.3. Thus, Alice concludes that the distance between Earth and Proxima Centauri is only 0.6ly instead of 4.2ly. The distance that she observes is contracted compared to the “proper distance” between Earth and Proxima (the distance measured when we are at rest relative to Earth and Proxima).
Discussion
In this example we saw, again, how the time that one measures depends on the frame of reference. In particular, if one can build spaceships that goes close to the speed of light, one can cover large distances in the Universe without ageing much. We also saw that length contraction is a necessary corollary to time-dilation. Objects appear contracted when they move, relative to their length when they are measured at rest (their “rest length” or their “proper length”).
One interesting issue uncovered by Example 24.3.2 is the so-called “twin-paradox”. Imagine that Alice has a twin brother, Brice, that remains on Earth. Alice travels to Proxima Centauri and back (return trip), and will have aged by about 14 months, whereas Brice, will have aged by about 8.4 years (using the numbers in Example 24.3.2). However, Einstein’s first postulate implies that there are no special frames of reference that are at rest. We should be able to think about this situation from the perspective where Alice is at rest, and it is the Earth (with Brice on it), that moves away from her and then back. In this case, Alice is at rest, and she will conclude that it takes about 8.4 years for Brice to move away and come back, and that Brice would have aged by about 7 months. When Alice and Brice meet up again, clearly Alice cannot be both younger and older than Brice, so which one is it? (You will have to look this up, see associated question in the “Thinking about the material” section).

