24.4: Length Contraction
- Page ID
- 19554
As we saw in the examples from the previous section, time dilation implies “length contraction”. When an object is measured in a frame of reference that is at rest relative to the object, the length of the object, \(L\), is called the “rest length” or the “proper length” of the object. If that object is moving relative to an observer, the observer will measure the object to be shorter, and have a “contracted length”, \(L'\), given by:
\[L'=L\sqrt{a-\frac{v^{2}}{c^{2}}}=\frac{L}{\gamma}\]
In Example 24.3.2, Alice measured a contracted distance between Earth and Proxima Centauri, as she was in a frame of reference that is moving relative to the Earth-Proxima Centauri reference frame. One point that is important to note is that length contraction only occurs along the direction parallel to the direction of motion.
A square painting hanging in a museum has a side with a length of \(1\text{m}\). If you view the stationary painting from a train moving in the horizontal direction at a speed of \(0.85c\), what is the surface area of the painting that you measure?
Solution
Since your train is moving horizontally, only the horizontal dimension of the painting will be contracted. The gamma factor is given by:
\[\begin{aligned} \gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} =\frac{1}{\sqrt{1-0.85^2}}=1.9\end{aligned}\]
Thus, the horizontal side of the painting will have a contracted length:
\[\begin{aligned} L'=\frac{L}{\gamma}=\frac{(1\text{m})}{(1.9)}=0.53\text{m}\end{aligned}\]
The area of the painting, as measured in the moving frame of reference, is given by:
\[\begin{aligned} A= (1\text{m})(0.53\text{m})=0.53\text{m}^{2}\end{aligned}\]
What speed must an object travel in order for it to appear \(1\)% shorter
- \(0.01c\)
- \(0.14c\)
- \(0.99c\)
- \(0.65c\)
- Answer
-
B.
In these types of problems, it is important to keep track of which reference frame gives us the proper length and which gives us the proper time. I recommend taking a minute at the beginning of each problem to think about this, and jot it down at the start of your solution. Take the example in which our friend Alice travels from Earth to Proxima Centuri on a spaceship. We are dealing with Earth's frame of reference, which I will call \(E\), and the Alice's frame of reference, which I will call \(A\). We are interested in the time elapsed on the spaceship and the distance to Proxima Centuri. The Earth is moving relative to the spaceship's clock and is stationary relative to Proxima Centuri. Thus, frame \(E\) gives us the dilated time, \(\Delta t'\), and the proper length, \(L\). Alice is stationary relative to the spaceship's clock and is moving relative to Proxima Centuri. Thus, frame \(A\) gives us the proper time, \(\Delta t\), and the contracted length, \(L'\).
At the top of my solution, I would write:
\[\begin{align*}
\textrm{Frame}\, E: L, \Delta t'\\[4pt]
\textrm{Frame}\, A: L', \Delta t
\end{align*}\]
To check that we got this right, the speed of the spaceship should not change depending on the reference frame. In the Earth's frame of reference, the velocity is given by \(v=L/\Delta t'\). In Alice's frame, it is given by \(v=L'/\Delta t\), or, using the gamma factor: \(v=(L/\gamma)/(\Delta t'/\gamma)=L/\Delta t'\), as expected.
Length contraction also allows us to discuss a famous paradox (the “barn”, or “ladder” or “barn-pole” paradox). Consider a train that has a rest length of \(500\text{m}\), traveling at a speed such that \(\gamma = 2.5\). As the train goes by, from Earth, it appears to have a (contracted) length:
\[\begin{aligned} L'_{train}=\frac{(500\text{m})}{2.5}=200\text{m}\end{aligned}\]
Suppose that there is a tunnel on Earth that is exactly \(200\text{m}\) long, so that the train, when contracted, will fit in the tunnel. When the train passes, an operator briefly closes (and re-opens) the doors at the ends of the tunnel, briefly “capturing” the train, and since the train is contracted, it never hits any of the doors, and all is fine.
From the train’s frame of reference, the train has a proper length of \(500\text{m}\), and the tunnel is contracted to a length of:
\[\begin{aligned} L'_{tunnel}=\frac{(200\text{m})}{(2.5)}=80\text{m}\end{aligned}\]
Thus, from the train’s perspective, if the doors of the tunnel are closed, there is no way that the \(500\text{m}\) long train can ever fit in the \(80\text{m}\) long tunnel, as illustrated in Figure \(\PageIndex{1}\). So what happens when the operator on Earth closes the doors of the tunnel to briefly “capture” the train?
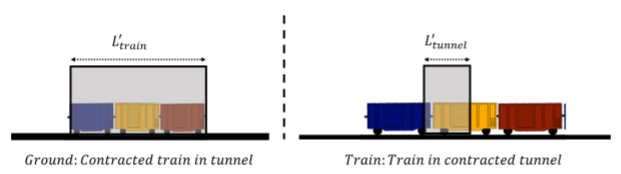
Clearly, people on the Earth and people on the train have to agree on whether the train was destroyed by the tunnel doors. The operator on Earth can clearly close both doors of the tunnel when the train is inside and not destroy the train. Hence, people on the train must agree that the train never collided with the doors, and that the doors were closed. The answer to this paradox lies in the fact that simultaneity is relative. The tunnel operator believes that she has closed the two doors of the tunnel at exactly the same time, precisely when the contracted train is lined up with the tunnel. However, to people on the train, in a different frame of reference, the doors did not close at the same time, since events that are simultaneous in one frame of reference are not necessarily simultaneous in a different frame of reference. To people on the train, there was never a time when the train was in the tunnel and both doors were closed at the same time!
Referring to the above paradox, to people on the train, which tunnel door closes first?
- The door at the entrance of the tunnel closes first.
- The door at the exit of the tunnel closes first.
- Answer
-
B.