24.2: Einstein’s postulates
( \newcommand{\kernel}{\mathrm{null}\,}\)
Albert Einstein was the first to provide a complete description of how to deal with the issues that arise from Maxwell’s equations when these are examined in different inertial frames of reference. The Theory of Special Relativity, is based on Einstein’s two postulates:
- The laws of physics are the same in all inertial reference frames. There is no experiment that can be performed to determine whether one is at rest or moving with constant velocity.
- The speed of light propagating in vacuum is the same in all inertial reference frames. Any observer in an inertial frame of reference, regardless of their velocity, will measure that light has a speed of c, when it propagates in vacuum.
These postulates are equivalent to the assumptions that we made above to model the force between the two wires (we stated that the constants, ϵ0 and μ0, were independent of reference frame, instead of c). While the first postulate is perhaps “acceptable” to our common sense, the second one grossly defies common intuition. Consider two archers, as illustrated in Figure 24.2.1.
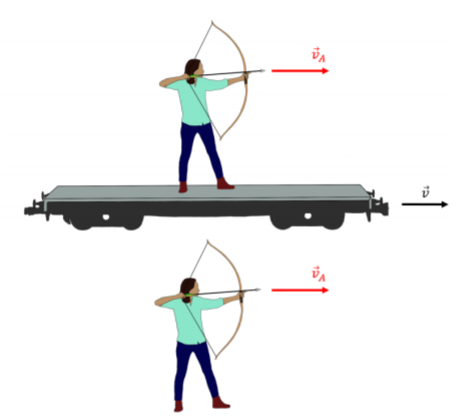
Both archers can fire an arrow with a speed, vA. One archer fires her arrow from the ground, at a target on the ground, and that arrow will hit the target with a speed, vA. The other archer is located on a train that is moving with speed v, in the same direction that she wishes to shoot her arrow. She measures her arrow to leave her bow with speed, vA, but, as seen from the ground (and from the target), her arrow has a speed vA+v, and it will hit the target with a higher speed, as expected.
Now, consider two space cops that instead fire a pulse of laser light at a target on the ground, as illustrated in Figure 24.2.2.
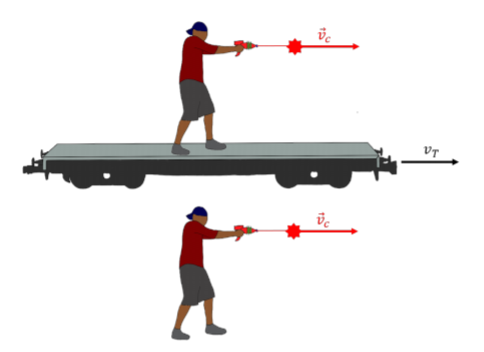
In this case, according to Einstein’s second postulate, the speed of the pulses as measured on the ground (by the target), will be c, regardless of whether one of the pulses was fired from a moving train. This is truly strange and not compatible with our experience. Imagine that the train is moving close to the speed of light. The space cop on the train would fire a laser pulse that he would observe to move away from him at the speed of light. When observed from the ground, we will see the pulse of light moves away from him very slowly, since he is on a train going at almost the speed of light.
Simultaneity
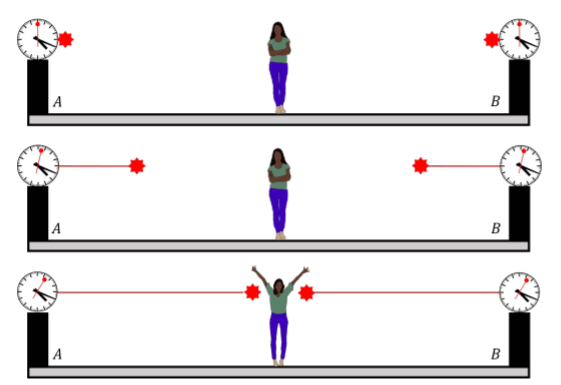
As a first consequence of Einstein’s postulates, let us consider the notion of simultaneity. Figure 24.2.3 shows Alice on the platform of a train station. Alice is midway between two clocks, A and B. Both identical clocks were configured so that they send a pulse of laser light when the time is 20 minutes past four o’clock. Since Alice is midway between the clocks, if they emit their pulses of light at the same time, then Alice will see two pulses of light arrive at her location at the same time. She signals that the two pulses of light have reached her at the same time by raising her hands.
Brice is located on a train that is traveling with speed, v, in the direction from clock A to clock B, as illustrated in Figure 24.2.4. He sees Alice and the platform moving towards him.
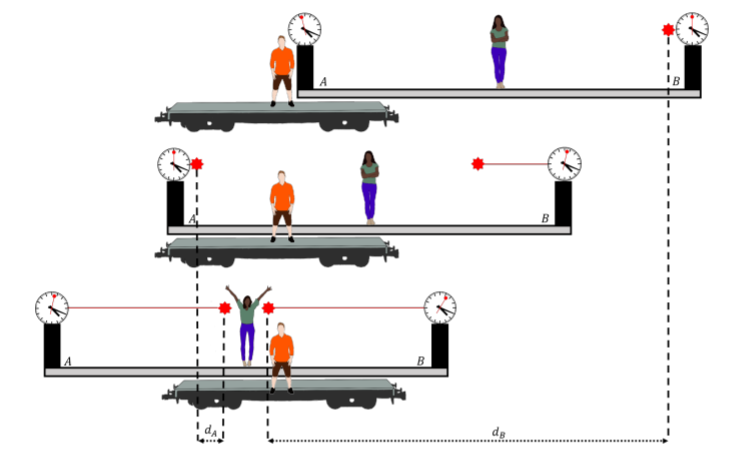
Brice must agree that the two pulses arrived at Alice’s location at the same time, since he can also see her raise her hands. In Brice’s frame of reference, the two pulses of light must travel with the speed of light (Einstein’s second postulate). Once the pulse of light has been emitted from clock B, Brice observes that Alice is moving away from the location of where the pulse was emitted, so that pulse must travel a large distance, dB. On the other hand, once the pulse from clock A is emitted, Brice observes that Alice moves towards where the pulse was emitted, so it only needs to travel a shorter distance, dA, in order to reach Alice. Thus, for both pulses to arrive at Alice at the same time and travel at the speed of light, the pulse from clock B had to be emitted first, according to Brice.
That is, while Alice measures the clocks to be synchronized and emit pulses at the same time, Brice measures that clock B is running ahead of clock A. The two observers, Alice and Brice, in different reference frames, cannot agree on whether two events are simultaneous. Even worse, if a third observer, , is located on a train going in the opposite direction from Brice’s train, she will conclude that the pulse from clock A was emitted earlier than the pulse from clock B. A consequence of Einstein’s postulates is that observers in different frames of reference will not agree on whether two events happen at the same time, and in some cases, as the one we illustrated, the observers will not agree on which event happened first. Think of the implications for causality!

