8.5: The Exclusion Principle and the Periodic Table
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain the importance of Pauli’s exclusion principle to an understanding of atomic structure and molecular bonding
- Explain the structure of the periodic table in terms of the total energy, orbital angular momentum, and spin of individual electrons in an atom
- Describe the electron configuration of atoms in the periodic table
So far, we have studied only hydrogen, the simplest chemical element. We have found that an electron in the hydrogen atom can be completely specified by five quantum numbers:
- n:principal quantum number
- l: angular momentum quantum number
- m: angular momentum projection quantum number
- s: spin quantum number
- ms: spin projection quantum number
To construct the ground state of a neutral multi-electron atom, imagine starting with a nucleus of charge Ze (that is, a nucleus of atomic number Z) and then adding Z electrons one by one. Assume that each electron moves in a spherically symmetrical electric field produced by the nucleus and all other electrons of the atom. The assumption is valid because the electrons are distributed randomly around the nucleus and produce an average electric field (and potential) that is spherically symmetrical. The electric potential U(r) for each electron does not follow the simple −1/r form because of interactions between electrons, but it turns out that we can still label each individual electron state by quantum numbers, (n,l,m,s,ms). (The spin quantum number s is the same for all electrons, so it will not be used in this section.)
The structure and chemical properties of atoms are explained in part by Pauli’s exclusion principle: No two electrons in an atom can have the same values for all four quantum numbers (n,l,m,ms). This principle is related to two properties of electrons: All electrons are identical (“when you’ve seen one electron, you’ve seen them all”) and they have half-integral spin (s=1/2). Sample sets of quantum numbers for the electrons in an atom are given in Table 8.5.1. Consistent with Pauli’s exclusion principle, no two rows of the table have the exact same set of quantum numbers.
| n | l | m | ms | Subshell symbol | No. of electrons: subshell | No. of electrons: shell |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | ½ | 1s | 2 | 2 |
| 1 | 0 | 0 | –½ | |||
| 2 | 0 | 0 | ½ | 2s | 2 | 8 |
| 2 | 0 | 0 | –½ | |||
| 2 | 1 | –1 | ½ | 2p | 6 | |
| 2 | 1 | –1 | –½ | |||
| 2 | 1 | 0 | ½ | |||
| 2 | 1 | 0 | –½ | |||
| 2 | 1 | 1 | ½ | |||
| 2 | 1 | 1 | –½ | |||
| 3 | 0 | 0 | ½ | 3s | 2 | 18 |
| 3 | 0 | 0 | –½ | |||
| 3 | 1 | –1 | ½ | 3p | 6 | |
| 3 | 1 | –1 | –½ | |||
| 3 | 1 | 0 | ½ | |||
| 3 | 1 | 0 | –½ | |||
| 3 | 1 | 1 | ½ | |||
| 3 | 1 | 1 | –½ | |||
| 3 | 2 | –2 | ½ | 3d | 10 | |
| 3 | 2 | –2 | –½ | |||
| 3 | 2 | –1 | ½ | |||
| 3 | 2 | –1 | –½ | |||
| 3 | 2 | 0 | ½ | |||
| 3 | 2 | 0 | –½ | |||
| 3 | 2 | 1 | ½ | |||
| 3 | 2 | 1 | –½ | |||
| 3 | 2 | 2 | ½ | |||
| 3 | 2 | 2 | –½ |
Electrons with the same principal quantum number n are said to be in the same shell, and those that have the same value of l are said to occupy the same subshell. An electron in the n=1 state of a hydrogen atom is denoted 1s, where the first digit indicates the shell (n=1) and the letter indicates the subshell (s,p,d,f,... correspond to l=0,1,2,3,...). Two electrons in the n=1 state are denoted as 1s2, where the superscript indicates the number of electrons. An electron in the n=2 state with l=1 is denoted 2p. The combination of two electrons in the n=2 and l=0 state, and three electrons in the n=2 and l=1 state is written as 2s22p3, and so on. This representation of the electron state is called the electron configuration of the atom. The electron configurations for several atoms are given in Table 8.5.2. Electrons in the outer shell of an atom are called valence electrons. Chemical bonding between atoms in a molecule are explained by the transfer and sharing of valence electrons.
| Element | Electron Configuration | Spin Alignment |
|---|---|---|
| H | 1s1 | (↑) |
| He | 1s2 | (↑↓) |
| Li | 1s22s1 | (↑) |
| Be | 1s22s2 | (↑↓) |
| B | 1s22s22p1 | (↑↓)(↑) |
| C | 1s22s22p2 | (↑↓)(↑)(↑) |
| N | 1s22s22p3 | (↑↓)(↑)(↑)(↑) |
| O | 1s22s22p4 | (↑↓)(↑↓)(↑)(↑) |
| F | 1s22s22p5 | (↑↓)(↑↓)(↑↓)(↑) |
| Ne | 1s22s22p6 | (↑↓)(↑↓)(↑↓)(↑↓) |
| Na | 1s22s22p63s1 | (↑) |
| Mg | 1s22s22p63s2 | (↑↓) |
| Al | 1s22s22p63s13p1 | (↑↓)(↑) |
The maximum number of electrons in a subshell depends on the value of the angular momentum quantum number, l. For a given a value l, there are 2l+1 orbital angular momentum states. However, each of these states can be filled by two electrons (spin up and down, ↑↓). Thus, the maximum number of electrons in a subshell is
N=2(2l+1)=4l+2.
In the 2s (l=0) subshell, the maximum number of electrons is 2. In the 2p (l=1) subshell, the maximum number of electrons is 6. Therefore, the total maximum number of electrons in the n=2 shell (including both the l=0 and 1 subshells) is 2+6 or 8. In general, the maximum number of electrons in the nth shell is 2n2.
How many subshells are in the n=3 shell? Identify each subshell and calculate the maximum number of electrons that will fill each. Show that the maximum number of electrons that fill an atom is 2n2.
Strategy
Subshells are determined by the value of l; thus, we first determine which values of l are allowed, and then we apply the equation “maximum number of electrons that can be in a subshell=2(2l+1)” to find the number of electrons in each subshell.
Solution
Because n=3, we know that l can be 0, 1, or 2; thus, there are three possible subshells. In standard notation, they are labeled the 3s, 3p, and 3d subshells. We have already seen that two electrons can be in an s state, and six in a p state, but let us use the equation “maximum number of electrons that can be in a
subshell =2(2l+1)” to calculate the maximum number in each:
3s has l=0; thus, 2(2l+1)=2(0+1)=2
3p has l=1; thus, 2(2l+1)=2(2+1)=6
3d has l=2; thus, 2(2l+1)=2(4+1)=10
Total=18
(in the n=3 shell).
The equation “maximum number of electrons that can be in a shell = 2n2” gives the maximum number in the n=3 shell to be
Maximum number of electrons =2n2=2(3)2=2(9)=18.
Significance
The total number of electrons in the three possible subshells is thus the same as the formula 2n2. In standard (spectroscopic) notation, a filled n=3 shell is denoted as 3s23p63d10. Shells do not fill in a simple manner. Before the n=3 shell is completely filled, for example, we begin to find electrons in the n=4 shell.
The structure of the periodic table (Figure 8.5.1) can be understood in terms of shells and subshells, and, ultimately, the total energy, orbital angular momentum, and spin of the electrons in the atom. A detailed discussion of the periodic table is left to a chemistry course—we sketch only its basic features here. In this discussion, we assume that the atoms are electrically neutral; that is, they have the same number of electrons and protons. (Recall that the total number of protons in an atomic nucleus is called the atomic number, Z.)
First, the periodic table is arranged into columns and rows. The table is read left to right and top to bottom in the order of increasing atomic number \(Z\). Atoms that belong to the same column or chemical group share many of the same chemical properties. For example, the Li and Na atoms (in the first column) bond to other atoms in a similar way. The first row of the table corresponds to the 1s (l=0) shell of an atom.
Consider the hypothetical procedure of adding electrons, one by one, to an atom. For hydrogen (H) (upper left), the 1s shell is filled with either a spin up or down electron (↑ or ↓). This lone electron is easily shared with other atoms, so hydrogen is chemically active. For helium (He) (upper right), the 1s shell is filled with both a spin up and a spin down (↑↓) electron. This “fills” the 1s shell, so a helium atom tends not to share electrons with other atoms. The helium atom is said to be chemically inactive, inert, or noble; likewise, helium gas is said to be an inert gas or noble gas.
Build an atom by adding and subtracting protons, neutrons, and electrons. How does the element, charge, and mass change? Visit PhET Explorations: Build an Atom to explore the answers to these questions.
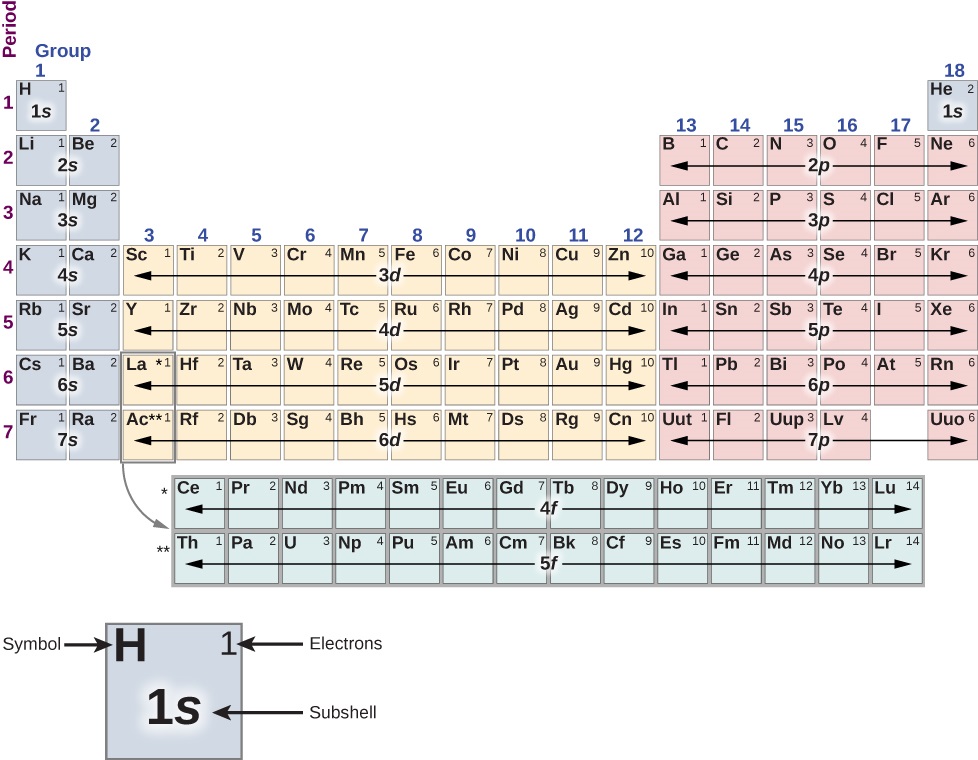
The second row corresponds to the 2s and 2p subshells. For lithium (Li) (upper left), the 1s shell is filled with a spin-up and spin-down electron (↑↓) and the 2s shell is filled with either a spin-up or -down electron (↑or↓). Its electron configuration is therefore 1s22s1 or [He]2s, where [He] indicates a helium core. Like hydrogen, the lone electron in the outermost shell is easily shared with other atoms. For beryllium (Be), the 2s shell is filled with a spin-up and -down electron (↑↓), and has the electron configuration [He]2s2.
Next, we look at the right side of the table. For boron (B), the 1s and 2s shells are filled and the 2p (l=1) shell contains either a spin up or down electron (↑or↓). From carbon (C) to neon (N), we the fill the 2p shell. The maximum number of electrons in the 2p shells is 4l+2=4(2)+2=6. For neon (Ne), the 1s shell is filled with a spin-up and spin-down electron (↑↓), and the 2p shell is filled with six electrons (↑↓↑↓↑↓). This “fills” the 1s, 2s, and 2p subshells, so like helium, the neon atom tends not to share electrons with other atoms.
The process of electron filling repeats in the third row. However, beginning in the fourth row, the pattern is broken. The actual order of order of electron filling is given by
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s,...
Notice that the 3d, 4d, 4f, and 5d subshells (in bold) are filled out of order; this occurs because of interactions between electrons in the atom, which so far we have neglected. The transition metals are elements in the gap between the first two columns and the last six columns that contain electrons that fill the d (l=1) subshell. As expected, these atoms are arranged in 4l+2=4(2)+2=10 columns. The structure of the periodic table can be understood in terms of the quantization of the total energy (n), orbital angular momentum (l), and spin (s). The first two columns correspond to the s (l=0) subshell, the next six columns correspond to the p (l=1) subshell, and the gap between these columns corresponds to the d (l=2) subshell.
The periodic table also gives information on molecular bonding. To see this, consider atoms in the left-most column (the so-called alkali metals including: Li, Na, and K). These atoms contain a single electron in the 2s subshell, which is easily donated to other atoms. In contrast, atoms in the second-to-right column (the halogens: for example, Cl, F, and Br) are relatively stingy in sharing electrons. These atoms would much rather accept an electron, because they are just one electron shy of a filled shell (“of being noble”).
Therefore, if a Na atom is placed in close proximity to a Cl atom, the Na atom freely donates its 2s electron and the Cl atom eagerly accepts it. In the process, the Na atom (originally a neutral charge) becomes positively charged and the Cl (originally a neutral charge) becomes negatively charged. Charged atoms are called ions. In this case, the ions are Na+ and Cl−, where the superscript indicates charge of the ion. The electric (Coulomb) attraction between these atoms forms a NaCl (salt) molecule. A chemical bond between two ions is called an ionic bond. There are many kinds of chemical bonds. For example, in an oxygen molecule O2 electrons are equally shared between the atoms. The bonding of oxygen atoms is an example of a covalent bond.


