3.6: Heat Capacities of an Ideal Gas

Learning Objectives

By the end of this section, you will be able to:

• Define heat capacity of an ideal gas for a specific process
• Calculate the specific heat of an ideal gas for either an isobaric or isochoric process
• Explain the difference between the heat capacities of an ideal gas and a real gas
• Estimate the change in specific heat of a gas over temperature ranges

We learned about specific heat and molar heat capacity previously; however, we have not considered a process in which heat is added. We do that in this section. First, we examine a process where the system has a constant volume, then contrast it with a system at constant pressure and show how their specific heats are related.

Let’s start with looking at Figure $\PageIndex{1}$, which shows two vessels A and B, each containing 1 mol of the same type of ideal gas at a temperature T and a volume V. The only difference between the two vessels is that the piston at the top of A is fixed, whereas the one at the top of B is free to move against a constant external pressure p. We now consider what happens when the temperature of the gas in each vessel is slowly increased to $T + dT$ with the addition of heat.

Figure $\PageIndex{1}$: Two vessels are identical except that the piston at the top of A is fixed, whereas that atop B is free to move against a constant external pressure p.

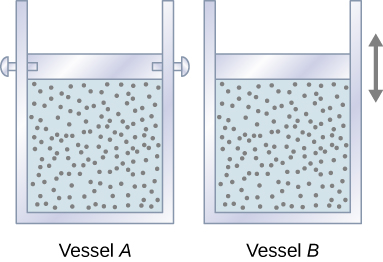
Since the piston of vessel A is fixed, the volume of the enclosed gas does not change. Consequently, the gas does no work, and we have from the first law

$$dE_{int} = dQ - dW = dQ. \nonumber$$

We represent the fact that the heat is exchanged at constant volume by writing

$$dQ = C_VndT, \nonumber$$ where $C_V$ is the molar heat capacity at constant volume of the gas. In addition, since $dE_{int} = dQ$ for this particular process,

$$dE_{int} = C_VndT. \label{3.9}$$

We obtained this equation assuming the volume of the gas was fixed. However, internal energy is a state function that depends on only the temperature of an ideal gas. Therefore, $dE_{int} = C_VndT$ gives the change in internal energy of an ideal gas for any process involving a temperature change dT.

When the gas in vessel B is heated, it expands against the movable piston and does work $dW = pdV$. In this case, the heat is added at constant pressure, and we write $$dQ = C_{p}ndT, \nonumber$$ where $C_p$ is the molar heat capacity at constant pressure of the gas. Furthermore, since the ideal gas expands against a constant pressure,

$$d(pV) = d(RnT) \nonumber$$ becomes $$pdV = RndT. \nonumber$$

Finally, inserting the expressions for dQ and pdV into the first law, we obtain

$$dE_{int} = dQ - pdV = (C_{p}n - Rn)dT. \nonumber$$

We have found $dE_{int}$ for both an isochoric and an isobaric process. Because the internal energy of an ideal gas depends only on the temperature, $dE_{int}$ must be the same for both processes. Thus,

$$C_{V}ndT = (C_{p}n - Rn)dT, \nonumber$$

and

$$C_p = C_V + R. \label{eq50}$$

The derivation of Equation $\ref{eq50}$ was based only on the ideal gas law. Consequently, this relationship is approximately valid for all dilute gases, whether monatomic like He, diatomic like $O_2$, or polyatomic like $CO_2$ or $NH_3$.

In the preceding chapter, we found the molar heat capacity of an ideal gas under constant volume to be

$$C_V = \dfrac{d}{2}R, \nonumber$$

where d is the number of degrees of freedom of a molecule in the system. Table $\PageIndex{1}$ shows the molar heat capacities of some dilute ideal gases at room temperature. The heat capacities of real gases are somewhat higher than those predicted by the expressions of $C_V$ and $C_p$ given in Equation $\ref{eq50}$. This indicates that vibrational motion in polyatomic molecules is significant, even at room temperature. Nevertheless, the difference in the molar heat capacities, $C_p - C_V$, is very close to R, even for the polyatomic gases.

Table $\PageIndex{1}$: Molar Heat Capacities of Dilute Ideal Gases at Room Temperature

		$C_p$	$C_V$	$C_p - C_V$
Type of Molecule	Gas	(J/mol K)	(J/mol K)	(J/mol K)
Monatomic	Ideal	$\frac{5}{2}R = 20.79$	$\frac{3}{2}R = 12.47$	$R = 8.31$
Diatomic	Ideal	$\frac{7}{2}R = 29.10$	$\frac{5}{2}R = 20.79$	$R = 8.31$
Polyatomic	Ideal	$4R = 33.26$	$3R = 24.04$	$R = 8.31$

Glossary

molar heat capacity at constant pressure

quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant pressure

molar heat capacity at constant volume

quantifies the ratio of the amount of heat added removed to the temperature while measuring at constant volume