5.5: Electric Field
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain the purpose of the electric field concept
- Describe the properties of the electric field
- Calculate the field of a collection of source charges of either sign
As we showed in the preceding section, the net electric force on a test charge is the vector sum of all the electric forces acting on it, from all of the various source charges, located at their various positions. But what if we use a different test charge, one with a different magnitude, or sign, or both? Or suppose we have a dozen different test charges we wish to try at the same location? We would have to calculate the sum of the forces from scratch. Fortunately, it is possible to define a quantity, called the electric field, which is independent of the test charge. It only depends on the configuration of the source charges, and once found, allows us to calculate the force on any test charge.
Defining a Field
Suppose we have N source charges q1,q2,q3,...qN located at positions →r1,→r2,→r3,...→rN, applying N electrostatic forces on a test charge Q. The net force on Q is
→F=→F1+→F2+→F3+...+→FN=14πϵ0(Qq1r21ˆr1+Qq2r22ˆr2+Qq3r23ˆr3+...+QqNr21ˆrN)=Q[14πϵ0(q1r21ˆr1+q2r22ˆr2+q3r23ˆr3+...+qNr21ˆrN)]
We can rewrite this as
→F=Q→E
where
→E≡14πϵ0(q1r21ˆr1+q2r22ˆr2+q3r23ˆr3+...+qNr21ˆrN)
or, more compactly,
This expression is called the electric field at position P=P(x,y,z) of the N source charges. Here, P is the location of the point in space where you are calculating the field and is relative to the positions →ri of the source charges (Figure 5.5.1). Note that we have to impose a coordinate system to solve actual problems.
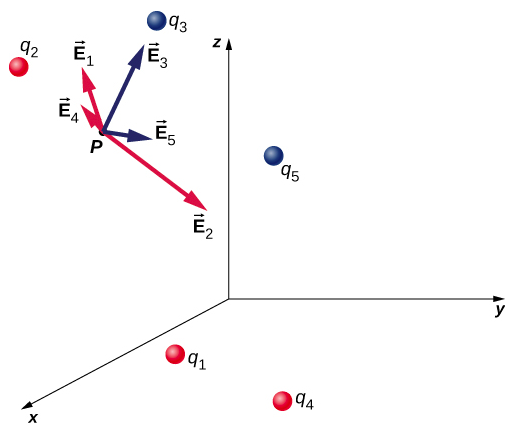
Notice that the calculation of the electric field makes no reference to the test charge. Thus, the physically useful approach is to calculate the electric field and then use it to calculate the force on some test charge later, if needed. Different test charges experience different forces Equation ???, but it is the same electric field Equation ???. That being said, recall that there is no fundamental difference between a test charge and a source charge; these are merely convenient labels for the system of interest. Any charge produces an electric field; however, just as Earth’s orbit is not affected by Earth’s own gravity, a charge is not subject to a force due to the electric field it generates. Charges are only subject to forces from the electric fields of other charges.
In this respect, the electric field →E of a point charge is similar to the gravitational field →g of Earth; once we have calculated the gravitational field at some point in space, we can use it any time we want to calculate the resulting force on any mass we choose to place at that point. In fact, this is exactly what we do when we say the gravitational field of Earth (near Earth’s surface) has a value of 9.81m/s2 and then we calculate the resulting force (i.e., weight) on different masses. Also, the general expression for calculating →g at arbitrary distances from the center of Earth (i.e., not just near Earth’s surface) is very similar to the expression for E:
→g=GMr2ˆr
where G is a proportionality constant, playing the same role for →g as 14πϵ0 does for →E. The value of →g is calculated once and is then used in an endless number of problems.
To push the analogy further, notice the units of the electric field: From F=QE, the units of E are newtons per coulomb, N/C, that is, the electric field applies a force on each unit charge. Now notice the units of g: From w=mg the units of g are newtons per kilogram, N/kg, that is, the gravitational field applies a force on each unit mass. We could say that the gravitational field of Earth, near Earth’s surface, has a value of 9.81 N/kg.
The Meaning of "Field"
Recall from your studies of gravity that the word “field” in this context has a precise meaning. A field, in physics, is a physical quantity whose value depends on (is a function of) position, relative to the source of the field. In the case of the electric field, Equation ??? shows that the value of →E (both the magnitude and the direction) depends on where in space the point P is located, measured from the locations →ri of the source charges qi.
In addition, since the electric field is a vector quantity, the electric field is referred to as a vector field. (The gravitational field is also a vector field.) In contrast, a field that has only a magnitude at every point is a scalar field. The temperature in a room is an example of a scalar field. It is a field because the temperature, in general, is different at different locations in the room, and it is a scalar field because temperature is a scalar quantity.
Also, as you did with the gravitational field of an object with mass, you should picture the electric field of a charge-bearing object (the source charge) as a continuous, immaterial substance that surrounds the source charge, filling all of space—in principle, to ±∞ in all directions. The field exists at every physical point in space. To put it another way, the electric charge on an object alters the space around the charged object in such a way that all other electrically charged objects in space experience an electric force as a result of being in that field. The electric field, then, is the mechanism by which the electric properties of the source charge are transmitted to and through the rest of the universe. (Again, the range of the electric force is infinite.)
We will see in subsequent chapters that the speed at which electrical phenomena travel is the same as the speed of light. There is a deep connection between the electric field and light.
Superposition
Yet another experimental fact about the field is that it obeys the superposition principle. In this context, that means that we can (in principle) calculate the total electric field of many source charges by calculating the electric field of only q1 at position P, then calculate the field of q2 at P, while—and this is the crucial idea—ignoring the field of, and indeed even the existence of, q1. We can repeat this process, calculating the field of each individual source charge, independently of the existence of any of the other charges. The total electric field, then, is the vector sum of all these fields. That, in essence, is what Equation ??? says.
In the next section, we describe how to determine the shape of an electric field of a source charge distribution and how to sketch it.
The Direction of the Field
Equation ??? enables us to determine the magnitude of the electric field, but we need the direction also. We use the convention that the direction of any electric field vector is the same as the direction of the electric force vector that the field would apply to a positive test charge placed in that field. Such a charge would be repelled by positive source charges (the force on it would point away from the positive source charge) but attracted to negative charges (the force points toward the negative source).
By convention, all electric fields →E point away from positive source charges and point toward negative source charges.
Download the Electric Field of Dreams PhET simulation and add charges to the and see how they react to the electric field. Turn on a background electric field and adjust the direction and magnitude.
In an ionized helium atom, the most probable distance between the nucleus and the electron is r=26.5×10−12m. What is the electric field due to the nucleus at the location of the electron?
Strategy
Note that although the electron is mentioned, it is not used in any calculation. The problem asks for an electric field, not a force; hence, there is only one charge involved, and the problem specifically asks for the field due to the nucleus. Thus, the electron is a red herring; only its distance matters. Also, since the distance between the two protons in the nucleus is much, much smaller than the distance of the electron from the nucleus, we can treat the two protons as a single charge +2e (Figure 5.5.2).
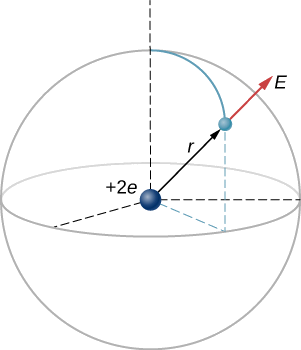
Solution
The electric field is calculated by
→E=14πϵ0N∑i=1qir2iˆri.
Since there is only one source charge (the nucleus), this expression simplifies to
→E=14πϵ0qr2ˆr.
Here, q=2e=2(1.6×10−19C) (since there are two protons) and r is given; substituting gives
→E=14π(8.85×10−12C2N⋅m2)2(1.6×10−19C)26.5×10−12m)2ˆr=4.1×1012NCˆr.
The direction of →E is radially away from the nucleus in all directions. Why? Because a positive test charge placed in this field would accelerate radially away from the nucleus (since it is also positively charged), and again, the convention is that the direction of the electric field vector is defined in terms of the direction of the force it would apply to positive test charges.
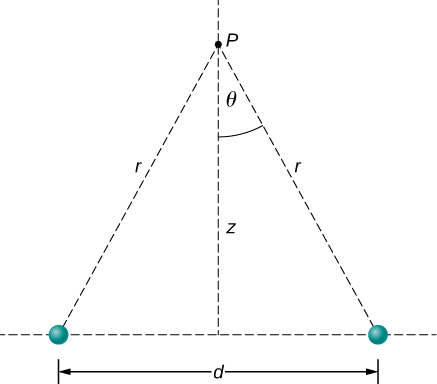
- Find the electric field (magnitude and direction) a distance z above the midpoint between two equal charges +q that are a distance d apart (Figure 5.5.3). Check that your result is consistent with what you’d expect when z≫d.
- The same as part (a), only this time make the right-hand charge −q instead of +q.
Strategy
We add the two fields as vectors, per Equation ???. Notice that the system (and therefore the field) is symmetrical about the vertical axis; as a result, the horizontal components of the field vectors cancel. This simplifies the math. Also, we take care to express our final answer in terms of only quantities that are given in the original statement of the problem: q, z, d, and constants (π,ϵ0).
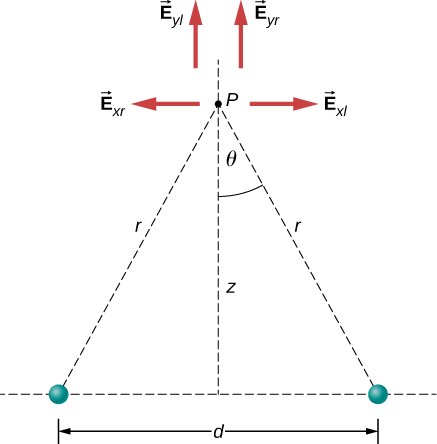
Solution
a. By symmetry, the horizontal (x)-components of →E cancel (Figure 5.5.4);
Ex=14πϵ0qr2sinθ−14πϵ0qr2sinθ=0.
The vertical (z)-component is given by
Ez=14πϵ0qr2cosθ+14πϵ0qr2cosθ=14πϵ02qr2cosθ.
Since none of the other components survive, this is the entire electric field, and it points in the ˆk direction. Notice that this calculation uses the principle of superposition; we calculate the fields of the two charges independently and then add them together.
What we want to do now is replace the quantities in this expression that we don’t know (such as r), or can’t easily measure (such as cosθ with quantities that we do know, or can measure. In this case, by geometry,
r2=z2+(d2)2
and
cosθ=zR=z[z2+(d2)2]1/2.
Thus, substituting,
→E(z)=14πϵ02q[z2+(d2)2]2z[z2+(d2)2]1/2ˆk.
Simplifying, the desired answer is
→E(z)=14πϵ02qz[z2+(d2)2]3/2ˆk.
b. If the source charges are equal and opposite, the vertical components cancel because
Ez=14πϵ0qr2cosθ−14πϵ0qr2cosθ=0
and we get, for the horizontal component of →E.
→E(z)=14πϵ0qd[z2+(d2)2]3/2ˆi.
Significance
It is a very common and very useful technique in physics to check whether your answer is reasonable by evaluating it at extreme cases. In this example, we should evaluate the field expressions for the cases d=0,z≫d, and z→∞, and confirm that the resulting expressions match our physical expectations. Let’s do so:
Let’s start with Equation ???, the field of two identical charges. From far away (i.e., z>>d), the two source charges should “merge” and we should then “see” the field of just one charge, of size 2q. So, let z≫d; then we can neglect d2 in Equation ??? to obtain
limd→0→E=14πϵ02qz[z2]3/2ˆk=14πϵ02qzz3ˆk=14πϵ02qz2ˆk,
which is the correct expression for a field at a distance z away from a charge 2q.
Next, we consider the field of equal and opposite charges, Equation ???. It can be shown (via a Taylor expansion) that for d≪z≪∞, , this becomes
→E(z)=14πϵ0qdz3ˆi,
which is the field of a dipole, a system that we will study in more detail later. (Note that the units of →E are still correct in this expression, since the units of d in the numerator cancel the unit of the “extra” z in the denominator.) If z is very large (z→∞), then E→0, as it should; the two charges “merge” and so cancel out.
What is the electric field due to a single point particle?
- Answer
-
→E=14πϵ0qr2ˆr
Try this simulation of electric field hockey to get the charge in the goal by placing other charges on the field.


