9.4: Resistivity and Resistance
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Differentiate between resistance and resistivity
- Define the term conductivity
- Describe the electrical component known as a resistor
- State the relationship between resistance of a resistor and its length, cross-sectional area, and resistivity
- State the relationship between resistivity and temperature
What drives current? We can think of various devices—such as batteries, generators, wall outlets, and so on—that are necessary to maintain a current. All such devices create a potential difference and are referred to as voltage sources. When a voltage source is connected to a conductor, it applies a potential difference V that creates an electrical field. The electrical field, in turn, exerts force on free charges, causing current. The amount of current depends not only on the magnitude of the voltage, but also on the characteristics of the material that the current is flowing through. The material can resist the flow of the charges, and the measure of how much a material resists the flow of charges is known as the resistivity. This resistivity is crudely analogous to the friction between two materials that resists motion.
Resistivity
When a voltage is applied to a conductor, an electrical field →E is created, and charges in the conductor feel a force due to the electrical field. The current density →J that results depends on the electrical field and the properties of the material. This dependence can be very complex. In some materials, including metals at a given temperature, the current density is approximately proportional to the electrical field. In these cases, the current density can be modeled as
→J=σ→E,
where σ is the electrical conductivity. The electrical conductivity is analogous to thermal conductivity and is a measure of a material’s ability to conduct or transmit electricity. Conductors have a higher electrical conductivity than insulators. Since the electrical conductivity is σ=J/E, the units are
σ=|J||E|=A/m2V/m=AV⋅m.
Here, we define a unit named the ohm with the Greek symbol uppercase omega, Ω. The unit is named after Georg Simon Ohm, whom we will discuss later in this chapter. The Ω is used to avoid confusion with the number 0. One ohm equals one volt per amp: 1Ω=1V/A. The units of electrical conductivity are therefore (Ω⋅m)−1.
Conductivity is an intrinsic property of a material. Another intrinsic property of a material is the resistivity, or electrical resistivity. The resistivity of a material is a measure of how strongly a material opposes the flow of electrical current. The symbol for resistivity is the lowercase Greek letter rho, ρ, and resistivity is the reciprocal of electrical conductivity:
ρ=1σ.
The unit of resistivity in SI units is the ohm-meter (Ω⋅m). We can define the resistivity in terms of the electrical field and the current density.
ρ=EJ.
The greater the resistivity, the larger the field needed to produce a given current density. The lower the resistivity, the larger the current density produced by a given electrical field. Good conductors have a high conductivity and low resistivity. Good insulators have a low conductivity and a high resistivity. Table 9.4.1 lists resistivity and conductivity values for various materials.
| Material | Conductivity, σ (Ω⋅m)−1 | Resistivity, ρ (Ω⋅m) | Temperature Coefficient α (°\mathrm{C})^{-1} |
|---|---|---|---|
| Conductors | |||
| Silver | 6.29 \times 10^7 | 1.59 \times 10^{-8} | 0.0038 |
| Copper | 5.95 \times 10^7 | 1.68 \times 10^{-8} | 0.0039 |
| Gold | 4.10 \times 10^7 | 2.44 \times 10^{-8} | 0.0034 |
| Aluminum | 3.77 \times 10^7 | 2.65 \times 10^{-8} | 0.0039 |
| Tungsten | 1.79 \times 10^7 | 5.60 \times 10^{-8} | 0.0045 |
| Iron | 1.03 \times 10^7 | 9.71 \times 10^{-8} | 0.0065 |
| Platinum | 0.94 \times 10^7 | 10.60 \times 10^{-8} | 0.0039 |
| Steel | 0.50 \times 10^7 | 20.00 \times 10^{-8} | |
| Lead | 0.45 \times 10^7 | 22.00 \times 10^{-8} | |
| Manganin (Cu, Mn, Ni alloy) | 0.21 \times 10^7 | 48.20 \times 10^{-8} | 0.000002 |
| Constantan (Cu, Ni alloy) | 0.20 \times 10^7 | 49.00 \times 10^{-8} | 0.00003 |
| Mercury | 0.10 \times 10^7 | 98.00 \times 10^{-8} | 0.0009 |
| Nichrome (Ni, Fe, Cr alloy) | 0.10 \times 10^7 | 100.00 \times 10^{-8} | 0.0004 |
| Semiconductors [1] | |||
| Carbon (pure) | 2.86 \times 10^{4} | 3.50 \times 10^{-5} | -0.0005 |
| Carbon | (2.86 - 1.67) \times 10^{-6} | (3.5 - 60) \times 10^{-5} | -0.0005 |
| Germanium (pure) | 600 \times 10^{-3} | -0.048 | |
| Germanium | (1 - 600) \times 10^{-3} | -0.050 | |
| Silicon (pure) | 2300 | -0.075 | |
| Silicon | 0.1 - 2300 | -0.07 | |
| Insulators | |||
| Amber | 2.00 \times 10^{-15} | 5 \times 10^{14} | |
| Glass | 10^{-9} - 19^{-14} | 10^9 - 10^{14} | |
| Lucite | < 10^{-13} | > 10^{13} | |
| Mica | 10^{-11} - 10^{-15} | 10^{11} - 10^{15} | |
| Quartz (fused) | 1.33 \times 10^{-18} | 75 \times 10^{16} | |
| Rubber (hard) | 10^{-13} - 10^{-16} | 10^{13} - 10^{16} | |
| Sulfur | 10^{-15} | 10^{15} | |
| TeflonTM | < 10^{-13} | > 10^{13} | |
| Wood | 10^{-8} - 10^{-11} | 10^8 - 10^{11} | |
The materials listed in the table are separated into categories of conductors, semiconductors, and insulators, based on broad groupings of resistivity. Conductors have the smallest resistivity, and insulators have the largest; semiconductors have intermediate resistivity. Conductors have varying but large, free charge densities, whereas most charges in insulators are bound to atoms and are not free to move. Semiconductors are intermediate, having far fewer free charges than conductors, but having properties that make the number of free charges depend strongly on the type and amount of impurities in the semiconductor. These unique properties of semiconductors are put to use in modern electronics, as we will explore in later chapters.
Calculate the current density, resistance, and electrical field of a 5-m length of copper wire with a diameter of 2.053 mm (12-gauge) carrying a current of I = 10 \, \mathrm{mA}.
Strategy
We can calculate the current density by first finding the cross-sectional area of the wire, which is A = 3.31 \, \mathrm{mm}^2, and the definition of current density J = \dfrac{I}{A}. The resistance can be found using the length of the wire L = 5.00 \, \mathrm{m}, the area, and the resistivity of copper \rho = 1.68 \times 10^{-8} \Omega \cdot \mathrm{m}, where R = \rho \dfrac{L}{A}. The resistivity and current density can be used to find the electrical field.
Solution
First, we calculate the current density:
\begin {align*} J &= \dfrac{I}{A} \\[5pt] &= \dfrac{10 \times 10^{-3} \mathrm{A}}{3.31 \times 10^{-6} \mathrm{m}^2} \\[5pt] &= 3.02 \times 10^3 \dfrac{\mathrm{A}}{\mathrm{m}^2}. \end{align*}
The resistance of the wire is
\begin {align*}R &= \rho \dfrac{L}{A} \\[5pt] &= (1.68 \times 10^{-8} \Omega \cdot \mathrm{m}) \dfrac{5.00 \, \mathrm{m}}{3.31 \times 10^{-6}\mathrm{m}^2} \\[5pt] &= 0.025 \, \Omega.\end{align*}
Finally, we can find the electrical field:
\begin {align*}E &= \rho J \\[5pt] &= 1.68 \times 10^{-8} \Omega \cdot \mathrm{m} \left(3.02 \times 10^3 \dfrac{\mathrm{A}}{\mathrm{m}^2}\right) \\[5pt] &= 5.07 \times 10^{-5} \dfrac{\mathrm{V}}{\mathrm{m}}.\end{align*}
Significance
From these results, it is not surprising that copper is used for wires for carrying current because the resistance is quite small. Note that the current density and electrical field are independent of the length of the wire, but the voltage depends on the length.
Copper wires use routinely used for extension cords and house wiring for several reasons. Copper has the highest electrical conductivity rating, and therefore the lowest resistivity rating, of all nonprecious metals. Also important is the tensile strength, where the tensile strength is a measure of the force required to pull an object to the point where it breaks. The tensile strength of a material is the maximum amount of tensile stress it can take before breaking. Copper has a high tensile strength, 2 \times 10^8 \, \dfrac{\mathrm{N}}{\mathrm{m}^2}. A third important characteristic is ductility. Ductility is a measure of a material’s ability to be drawn into wires and a measure of the flexibility of the material, and copper has a high ductility. Summarizing, for a conductor to be a suitable candidate for making wire, there are at least three important characteristics: low resistivity, high tensile strength, and high ductility. What other materials are used for wiring and what are the advantages and disadvantages?
- Answer
-
Silver, gold, and aluminum are all used for making wires. All four materials have a high conductivity, silver having the highest. All four can easily be drawn into wires and have a high tensile strength, though not as high as copper. The obvious disadvantage of gold and silver is the cost, but silver and gold wires are used for special applications, such as speaker wires. Gold does not oxidize, making better connections between components. Aluminum wires do have their drawbacks. Aluminum has a higher resistivity than copper, so a larger diameter is needed to match the resistance per length of copper wires, but aluminum is cheaper than copper, so this is not a major drawback. Aluminum wires do not have as high of a ductility and tensile strength as copper, but the ductility and tensile strength is within acceptable levels. There are a few concerns that must be addressed in using aluminum and care must be used when making connections. Aluminum has a higher rate of thermal expansion than copper, which can lead to loose connections and a possible fire hazard. The oxidation of aluminum does not conduct and can cause problems. Special techniques must be used when using aluminum wires and components, such as electrical outlets, must be designed to accept aluminum wires.
View this interactive simulation to see what the effects of the cross-sectional area, the length, and the resistivity of a wire are on the resistance of a conductor. Adjust the variables using slide bars and see if the resistance becomes smaller or larger.
Temperature Dependence of Resistivity
Looking back at Table \PageIndex{1}, you will see a column labeled “Temperature Coefficient.” The resistivity of some materials has a strong temperature dependence. In some materials, such as copper, the resistivity increases with increasing temperature. In fact, in most conducting metals, the resistivity increases with increasing temperature. The increasing temperature causes increased vibrations of the atoms in the lattice structure of the metals, which impede the motion of the electrons. In other materials, such as carbon, the resistivity decreases with increasing temperature. In many materials, the dependence is approximately linear and can be modeled using a linear equation:
\rho \approx \rho_0 [1 + \alpha (T - T_0)], \nonumber
where \rho is the resistivity of the material at temperature T, \alpha is the temperature coefficient of the material, and \rho_0 is the resistivity at T_0, usually taken as T_0 = 20.00\, °\mathrm{C}.
Note also that the temperature coefficient \alpha is negative for the semiconductors listed in Table \PageIndex{1}, meaning that their resistivity decreases with increasing temperature. They become better conductors at higher temperature, because increased thermal agitation increases the number of free charges available to carry current. This property of decreasing \rho with temperature is also related to the type and amount of impurities present in the semiconductors.
Resistance
We now consider the resistance of a wire or component. The resistance is a measure of how difficult it is to pass current through a wire or component. Resistance depends on the resistivity. The resistivity is a characteristic of the material used to fabricate a wire or other electrical component, whereas the resistance is a characteristic of the wire or component.
To calculate the resistance, consider a section of conducting wire with cross-sectional area A, length L, and resistivity \rho. A battery is connected across the conductor, providing a potential difference \Delta V across it (Figure \PageIndex{1}). The potential difference produces an electrical field that is proportional to the current density, according to \vec{E} = \rho \vec{J}.
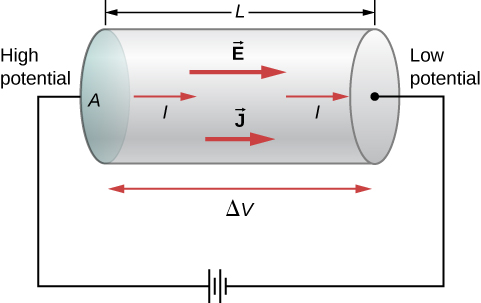
The magnitude of the electrical field across the segment of the conductor is equal to the voltage divided by the length, E = V/L, and the magnitude of the current density is equal to the current divided by the cross-sectional area, J = I/A. Using this information and recalling that the electrical field is proportional to the resistivity and the current density, we can see that the voltage is proportional to the current:
\begin{align*} E &= \rho J \\[4pt] \dfrac{V}{L} &= \rho \dfrac{I}{A} \\[4pt] V &= \left(\rho \dfrac{L}{A}\right) I. \end{align*}
The ratio of the voltage to the current is defined as the resistance R:
R \equiv \dfrac{V}{I}. \nonumber
The resistance of a cylindrical segment of a conductor is equal to the resistivity of the material times the length divided by the area:
R \equiv \dfrac{V}{I} = \rho \dfrac{L}{A}. \nonumber
The unit of resistance is the ohm, \Omega. For a given voltage, the higher the resistance, the lower the current.
Resistors
A common component in electronic circuits is the resistor. The resistor can be used to reduce current flow or provide a voltage drop. Figure \PageIndex{2} shows the symbols used for a resistor in schematic diagrams of a circuit. Two commonly used standards for circuit diagrams are provided by the American National Standard Institute (ANSI, pronounced “AN-see”) and the International Electrotechnical Commission (IEC). Both systems are commonly used. We use the ANSI standard in this text for its visual recognition, but we note that for larger, more complex circuits, the IEC standard may have a cleaner presentation, making it easier to read.

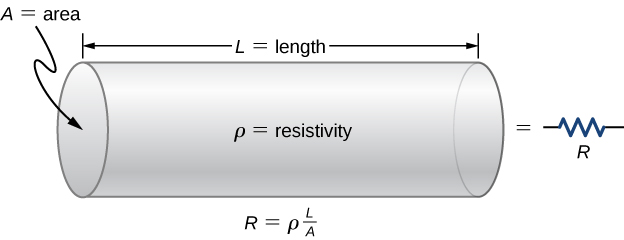
Material and shape dependence of resistance
A resistor can be modeled as a cylinder with a cross-sectional area A and a length L, made of a material with a resistivity \rho (Figure \PageIndex{3}). The resistance of the resistor is R = \rho \dfrac{L}{A}
The most common material used to make a resistor is carbon. A carbon track is wrapped around a ceramic core, and two copper leads are attached. A second type of resistor is the metal film resistor, which also has a ceramic core. The track is made from a metal oxide material, which has semiconductive properties similar to carbon. Again, copper leads are inserted into the ends of the resistor. The resistor is then painted and marked for identification. A resistor has four colored bands, as shown in Figure \PageIndex{4}.

Resistances range over many orders of magnitude. Some ceramic insulators, such as those used to support power lines, have resistances of 10^{12} \, \Omega or more. A dry person may have a hand-to-foot resistance of 10^5 \, \Omega whereas the resistance of the human heart is about 10^3 \, \Omega A meter-long piece of large-diameter copper wire may have a resistance of 10^{-5} \, \Omega, and superconductors have no resistance at all at low temperatures. As we have seen, resistance is related to the shape of an object and the material of which it is composed.
The resistance of an object also depends on temperature, since R_0 is directly proportional to \rho. For a cylinder, we know R = \rho \dfrac{L}{A}, so if L and A do not change greatly with temperature, R has the same temperature dependence as \rho. (Examination of the coefficients of linear expansion shows them to be about two orders of magnitude less than typical temperature coefficients of resistivity, so the effect of temperature on L and A is about two orders of magnitude less than on \rho.) Thus,
R = R_0(1 + \alpha \Delta T) \label{Tdep}
is the temperature dependence of the resistance of an object, where R_0 is the original resistance (usually taken to be T = 20.00\,°C and R is the resistance after a temperature change \Delta T. The color code gives the resistance of the resistor at a temperature of T = 20.00\,°C.
Numerous thermometers are based on the effect of temperature on resistance (Figure \PageIndex{5}). One of the most common thermometers is based on the thermistor, a semiconductor crystal with a strong temperature dependence, the resistance of which is measured to obtain its temperature. The device is small, so that it quickly comes into thermal equilibrium with the part of a person it touches.
Although caution must be used in applying \rho = \rho_0 (1 + \alpha \Delta T) and R = R_0(1 + \alpha \Delta T) for temperature changes greater than 100\,°C, for tungsten, the equations work reasonably well for very large temperature changes. A tungsten filament at 20\,°C has a resistance of 0.350 \, \Omega. What would the resistance be if the temperature is increased to 2850\,°C?
Strategy
This is a straightforward application of Equation \ref{Tdep}, since the original resistance of the filament is given as R_0 = 0.350 \, \Omega and the temperature change is \Delta T = 2830\,°C.
Solution
The resistance of the hotter filament R is obtained by entering known values into the above equation:
\begin{align*} R &= R_0(1 + \alpha \Delta T) \\[5pt] &= (0.350 \, \Omega)\left(1 + \left(\dfrac{4.5 \times 10^{-3}}{°C}\right)(2830\,°C)\right) \\[5pt] &= 4.8 \, \Omega \end{align*} \nonumber
Significance
Notice that the resistance changes by more than a factor of 10 as the filament warms to the high temperature and the current through the filament depends on the resistance of the filament and the voltage applied. If the filament is used in an incandescent light bulb, the initial current through the filament when the bulb is first energized will be higher than the current after the filament reaches the operating temperature.
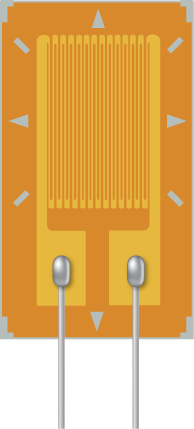
A strain gauge is an electrical device to measure strain, as shown below. It consists of a flexible, insulating backing that supports a conduction foil pattern. The resistance of the foil changes as the backing is stretched. How does the strain gauge resistance change? Is the strain gauge affected by temperature changes?
- Answer
-
The foil pattern stretches as the backing stretches, and the foil tracks become longer and thinner. Since the resistance is calculated as R = \rho \dfrac{L}{A}, the resistance increases as the foil tracks are stretched. When the temperature changes, so does the resistivity of the foil tracks, changing the resistance. One way to combat this is to use two strain gauges, one used as a reference and the other used to measure the strain. The two strain gauges are kept at a constant temperature
Long cables can sometimes act like antennas, picking up electronic noise, which are signals from other equipment and appliances. Coaxial cables are used for many applications that require this noise to be eliminated. For example, they can be found in the home in cable TV connections or other audiovisual connections. Coaxial cables consist of an inner conductor of radius r_i surrounded by a second, outer concentric conductor with radius r_o (Figure \PageIndex{6}). The space between the two is normally filled with an insulator such as polyethylene plastic. A small amount of radial leakage current occurs between the two conductors. Determine the resistance of a coaxial cable of length L.
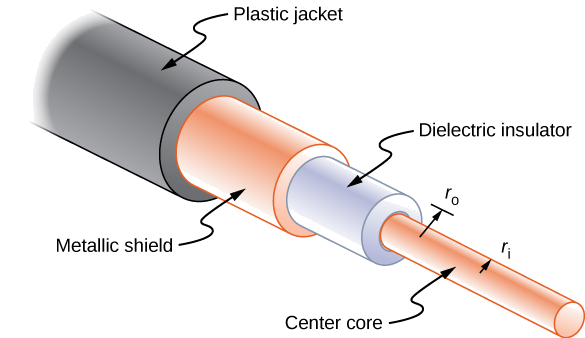
Strategy
We cannot use the equation R = \rho \dfrac{L}{A} directly. Instead, we look at concentric cylindrical shells, with thickness dr, and integrate.
Solution
We first find an expression for dR and then integrate from r_i to r_o,
\begin{align*} dR &= \dfrac{\rho}{A} dr \\[5pt] &= \dfrac{\rho}{2 \pi r L} dr, \end{align*}
Integrating both sides
\begin{align*} R &= \int_{r_i}^{r_o} dR \\[5pt] &= \int_{r_i}^{r_o} \dfrac{\rho}{2 \pi r L} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \int_{r_i}^{r_o} \dfrac{1}{r} dr \\[5pt] &= \dfrac{\rho}{2\pi L} \ln \dfrac{r_o}{r_i}.\end{align*}
Significance
The resistance of a coaxial cable depends on its length, the inner and outer radii, and the resistivity of the material separating the two conductors. Since this resistance is not infinite, a small leakage current occurs between the two conductors. This leakage current leads to the attenuation (or weakening) of the signal being sent through the cable.
The resistance between the two conductors of a coaxial cable depends on the resistivity of the material separating the two conductors, the length of the cable and the inner and outer radius of the two conductors. If you are designing a coaxial cable, how does the resistance between the two conductors depend on these variables?
- Answer
-
The longer the length, the smaller the resistance. The greater the resistivity, the higher the resistance. The larger the difference between the outer radius and the inner radius, that is, the greater the ratio between the two, the greater the resistance. If you are attempting to maximize the resistance, the choice of the values for these variables will depend on the application. For example, if the cable must be flexible, the choice of materials may be limited.
View this simulation to see how the voltage applied and the resistance of the material the current flows through affects the current through the material. You can visualize how the collisions of the electrons and the atoms of the material affect the temperature of the material.


