9.6: Band Theory of Solids
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe two main approaches to determining the energy levels of an electron in a crystal
- Explain the presence of energy bands and gaps in the energy structure of a crystal
- Explain why some materials are good conductors and others are good insulators
- Differentiate between an insulator and a semiconductor
The free electron model explains many important properties of conductors but is weak in at least two areas. First, it assumes a constant potential energy within the solid. (Recall that a constant potential energy is associated with no forces.) Figure \PageIndex{1} compares the assumption of a constant potential energy (dotted line) with the periodic Coulomb potential, which drops as -1/r at each lattice point, where r is the distance from the ion core (solid line). Second, the free electron model assumes an impenetrable barrier at the surface. This assumption is not valid, because under certain conditions, electrons can escape the surface—such as in the photoelectric effect. In addition to these assumptions, the free electron model does not explain the dramatic differences in electronic properties of conductors, semiconductors, and insulators. Therefore, a more complete model is needed.
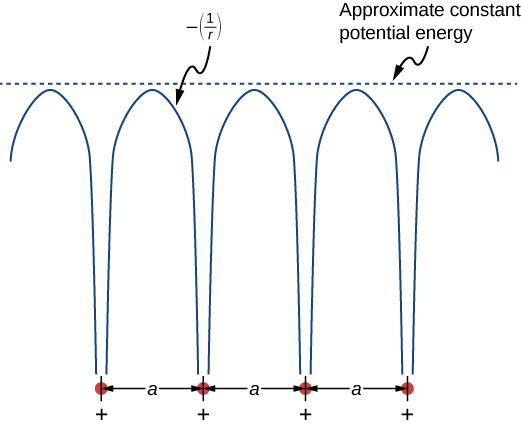
We can produce an improved model by solving Schrödinger’s equation for the periodic potential shown in Figure \PageIndex{1}. However, the solution requires technical mathematics far beyond our scope. We again seek a qualitative argument based on quantum mechanics to find a way forward.
We first review the argument used to explain the energy structure of a covalent bond. Consider two identical hydrogen atoms so far apart that there is no interaction whatsoever between them. Further suppose that the electron in each atom is in the same ground state: a 1s electron with an energy of -13.6 \, eV (ignore spin). When the hydrogen atoms are brought closer together, the individual wave functions of the electrons overlap and, by the exclusion principle, can no longer be in the same quantum state, which splits the original equivalent energy levels into two different energy levels. The energies of these levels depend on the interatomic distance, a (Figure \PageIndex{2a}).
If four hydrogen atoms are brought together, four levels are formed from the four possible symmetries—a single sine wave “hump” in each well, alternating up and down, and so on. In the limit of a very large number N of atoms, we expect a spread of nearly continuous bands of electronic energy levels in a solid (Figure \PageIndex{2c}). Each of these bands is known as an energy band. (The allowed states of energy and wave number are still technically quantized, but for large numbers of atoms, these states are so close together that they are consider to be continuous or “in the continuum.”)
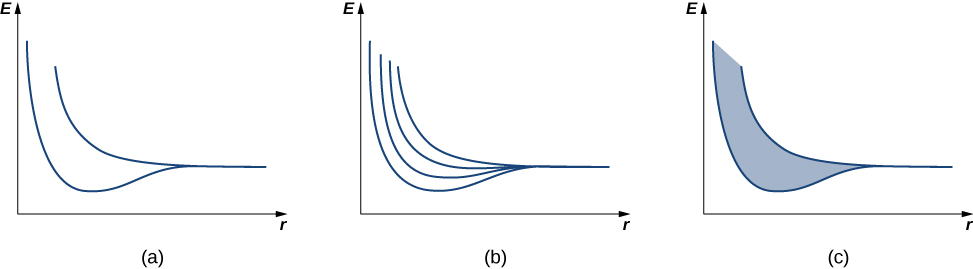
Energy bands differ in the number of electrons they hold. In the 1s and 2s energy bands, each energy level holds up to two electrons (spin up and spin down), so this band has a maximum occupancy of 2N electrons. In the 2p energy band, each energy level holds up to six electrons, so this band has a maximum occupancy of 6N electrons (Figure \PageIndex{3}).

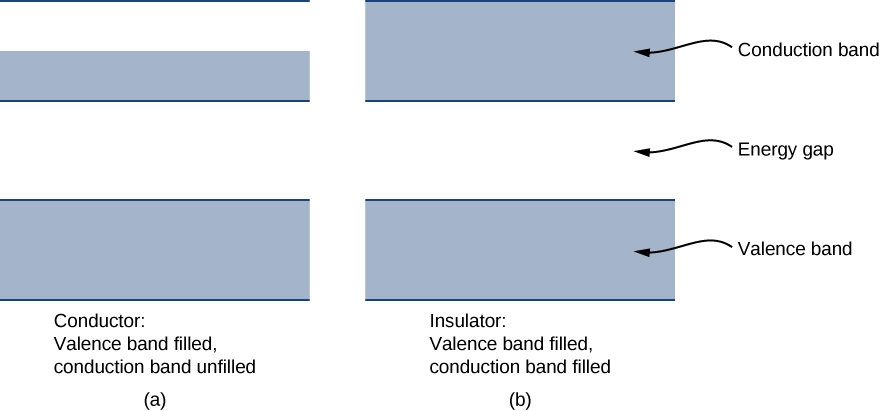
Each energy band is separated from the other by an energy gap. The electrical properties of conductors and insulators can be understood in terms of energy bands and gaps. The highest energy band that is filled is known as a valence band. The next available band in the energy structure is known as a conduction band. In a conductor, the highest energy band that contains electrons is partially filled, whereas in an insulator, the highest energy band containing electrons is completely filled. The difference between a conductor and insulator is illustrated in Figure \PageIndex{4}.
A conductor differs from an insulator in how its electrons respond to an applied electric field. If a significant number of electrons are set into motion by the field, the material is a conductor. In terms of the band model, electrons in the partially filled conduction band gain kinetic energy from the electric field by filling higher energy states in the conduction band. By contrast, in an insulator, electrons belong to completely filled bands. When the field is applied, the electrons cannot make such transitions (acquire kinetic energy from the electric field) due to the exclusion principle. As a result, the material does not conduct electricity.
Visit this simulation to learn about the origin of energy bands in crystals of atoms and how the structure of bands determines how a material conducts electricity. Explore how band structure creates a lattice of many wells.
A semiconductor has a similar energy structure to an insulator except it has a relatively small energy gap between the lowest completely filled band and the next available unfilled band. This type of material forms the basis of modern electronics. At T = 0 \, K, the semiconductor and insulator both have completely filled bands. The only difference is in the size of the energy gap (or band gap) Eg between the highest energy band that is filled (the valence band) and the next-higher empty band (the conduction band). In a semiconductor, this gap is small enough that a substantial number of electrons from the valence band are thermally excited into the conduction band at room temperature. These electrons are then in a nearly empty band and can respond to an applied field. As a general rule of thumb, the band gap of a semiconductor is about 1 eV. (Table \PageIndex{1} for silicon.) A band gap of greater than approximately 1 eV is considered an insulator. For comparison, the energy gap of diamond (an insulator) is several electron-volts.
| Material | Energy Gap E_g(eV) |
|---|---|
| Si | 1.14 |
| Ge | 0.67 |
| GaAs | 1.43 |
| GaP | 2.26 |
| GaSb | 0.69 |
| InAs | 0.35 |
| InP | 1.35 |
| InSb | 0.16 |
| C(diamond) | 5.48 |


