13.10: Electromagnetic Induction (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
13.2 Faraday’s Law
1. A stationary coil is in a magnetic field that is changing with time. Does the emf induced in the coil depend on the actual values of the magnetic field?
2. In Faraday’s experiments, what would be the advantage of using coils with many turns?
3. A copper ring and a wooden ring of the same dimensions are placed in magnetic fields so that there is the same change in magnetic flux through them. Compare the induced electric fields and currents in the rings.
4. Discuss the factors determining the induced emf in a closed loop of wire.
5. (a) Does the induced emf in a circuit depend on the resistance of the circuit?
(b) Does the induced current depend on the resistance of the circuit?
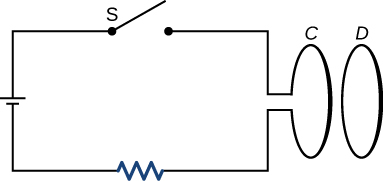
6. How would changing the radius of loop D shown below affect its emf, assuming C and D are much closer together compared to their radii?
7. Can there be an induced emf in a circuit at an instant when the magnetic flux through the circuit is zero?
8. Does the induced emf always act to decrease the magnetic flux through a circuit?
9. How would you position a flat loop of wire in a changing magnetic field so that there is no induced emf in the loop?
10. The normal to the plane of a single-turn conducting loop is directed at an angle θ to a spatially uniform magnetic field vecB. It has a fixed area and orientation relative to the magnetic field. Show that the emf induced in the loop is given by ε=(dB/dt)(Acosθ),where A is the area of the loop.
13.3 Lenz's Law
11. The circular conducting loops shown in the accompanying figure are parallel, perpendicular to the plane of the page, and coaxial.
(a) When the switch S is closed, what is the direction of the current induced in D?
(b) When the switch is opened, what is the direction of the current induced in loop D?

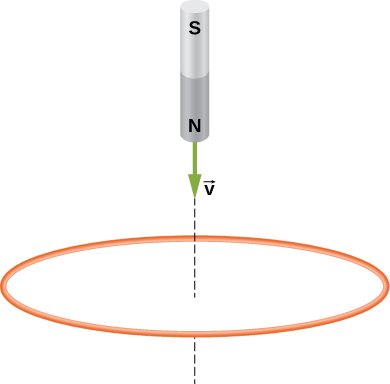
12. The north pole of a magnet is moved toward a copper loop, as shown below. If you are looking at the loop from above the magnet, will you say the induced current is circulating clockwise or counterclockwise?
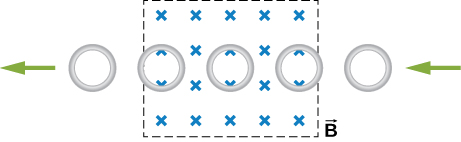
13. The accompanying figure shows a conducting ring at various positions as it moves through a magnetic field. What is the sense of the induced emf for each of those positions?
14. Show that ε and dΦm/dt have the same units.
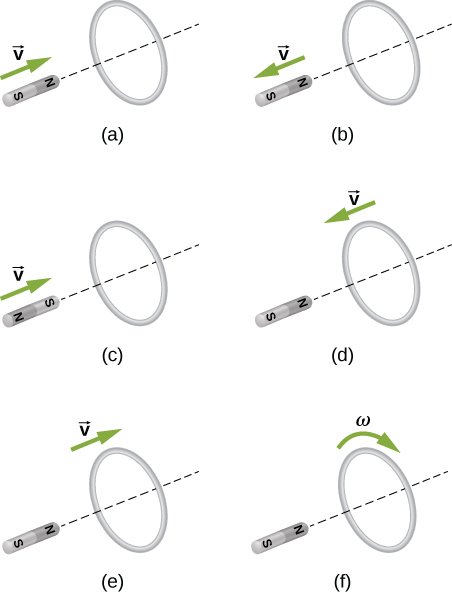
15. State the direction of the induced current for each case shown below, observing from the side of the magnet.
13.4 Motional Emf
16. A bar magnet falls under the influence of gravity along the axis of a long copper tube. If air resistance is negligible, will there be a force to oppose the descent of the magnet? If so, will the magnet reach a terminal velocity?
17. Around the geographic North Pole (or magnetic South Pole), Earth’s magnetic field is almost vertical. If an airplane is flying northward in this region, which side of the wing is positively charged and which is negatively charged?
18. A wire loop moves translationally (no rotation) in a uniform magnetic field. Is there an emf induced in the loop?
13.5 Induced Electric Fields
19. Is the work required to accelerate a rod from rest to a speed v in a magnetic field greater than the final kinetic energy of the rod? Why?
20. The copper sheet shown below is partially in a magnetic field. When it is pulled to the right, a resisting force pulls it to the left. Explain. What happen if the sheet is pushed to the left?
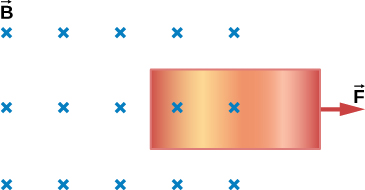
13.6 Eddy Currents
21. A conducting sheet lies in a plane perpendicular to a magnetic field →B that is below the sheet. If →B oscillates at a high frequency and the conductor is made of a material of low resistivity, the region above the sheet is effectively shielded from →B. Explain why. Will the conductor shield this region from static magnetic fields?
22. Electromagnetic braking can be achieved by applying a strong magnetic field to a spinning metal disk attached to a shaft.
(a) How can a magnetic field slow the spinning of a disk?
(b) Would the brakes work if the disk was made of plastic instead of metal?
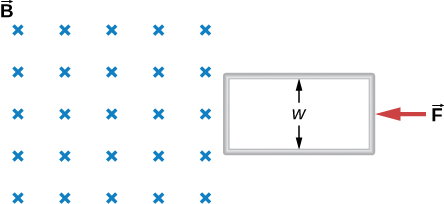
23. A coil is moved through a magnetic field as shown below. The field is uniform inside the rectangle and zero outside. What is the direction of the induced current and what is the direction of the magnetic force on the coil at each position shown?
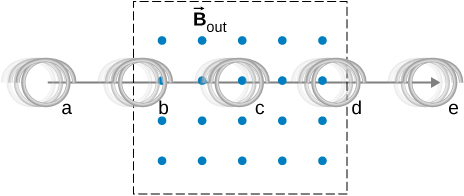
Problems
13.2 Faraday’s Law
24. A 50-turn coil has a diameter of 15 cm. The coil is placed in a spatially uniform magnetic field of magnitude 0.50 T so that the face of the coil and the magnetic field are perpendicular. Find the magnitude of the emf induced in the coil if the magnetic field is reduced to zero uniformly in
(a) 0.10 s,
(b) 1.0 s, and
(c) 60 s.
25. Repeat your calculations of the preceding problem’s time of 0.1 s with the plane of the coil making an angle of
(a) 30°,
(b) 60°, and
(c) 90° with the magnetic field.
26. A square loop whose sides are 6.0-cm long is made with copper wire of radius 1.0 mm. If a magnetic field perpendicular to the loop is changing at a rate of 5.0 mT/s, what is the current in the loop?
27. The magnetic field through a circular loop of radius 10.0 cm varies with time as shown below. The field is perpendicular to the loop. Plot the magnitude of the induced emf in the loop as a function of time.
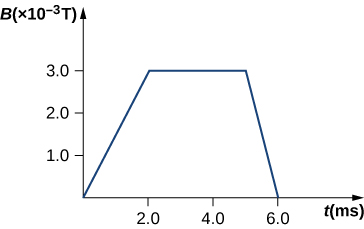
28. The accompanying figure shows a single-turn rectangular coil that has a resistance of 2.0Ω.2.0Ω. The magnetic field at all points inside the coil varies according to B=B0e−αt, where B0=0.25T and α=200Hz. What is the current induced in the coil at
(a) t=0.001s,
(b) 0.002 s,
(c) 2.0 s?
29. How would the answers to the preceding problem change if the coil consisted of 20 closely spaced turns?
30. A long solenoid with n=10 turns per centimeter has a cross-sectional area of 5.0cm2 and carries a current of 0.25 A. A coil with five turns encircles the solenoid. When the current through the solenoid is turned off, it decreases to zero in 0.050 s. What is the average emf induced in the coil?
31. A rectangular wire loop with length a and width b lies in the xy-plane, as shown below. Within the loop there is a time-dependent magnetic field given by →B(t)=C((xcosωt)ˆi+(ysinωt)ˆk), with →B(t) in tesla. Determine the emf induced in the loop as a function of time.
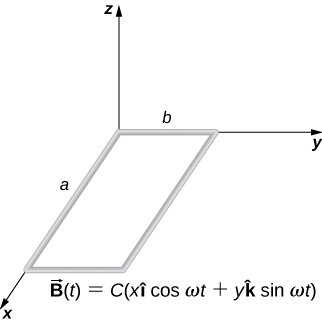
32. The magnetic field perpendicular to a single wire loop of diameter 10.0 cm decreases from 0.50 T to zero. The wire is made of copper and has a diameter of 2.0 mm and length 1.0 cm. How much charge moves through the wire while the field is changing?
13.3 Lenz's Law
33. A single-turn circular loop of wire of radius 50 mm lies in a plane perpendicular to a spatially uniform magnetic field. During a 0.10-s time interval, the magnitude of the field increases uniformly from 200 to 300 mT.
(a) Determine the emf induced in the loop.
(b) If the magnetic field is directed out of the page, what is the direction of the current induced in the loop?
34. When a magnetic field is first turned on, the flux through a 20-turn loop varies with time according to Φm=5.0t2−2.0t, where Φm is in milliwebers, t is in seconds, and the loop is in the plane of the page with the unit normal pointing outward.
(a) What is the emf induced in the loop as a function of time? What is the direction of the induced current at
(b) t = 0,
(c) 0.10,
(d) 1.0, and
(e) 2.0 s?
35. The magnetic flux through the loop shown in the accompanying figure varies with time according to Φm=2.00e−3tsin(120πt),where Φm is in milliwebers. What are the direction and magnitude of the current through the 5.00-Ω resistor at (a) t=0t=0; (b) t=2.17×10−2s, and (c) t=3.00s?
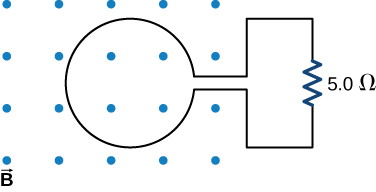
36. Use Lenz’s law to determine the direction of induced current in each case.
13.4 Motional Emf
37. An automobile with a radio antenna 1.0 m long travels at 100.0 km/h in a location where the Earth’s horizontal magnetic field is 5.5×10−5T. What is the maximum possible emf induced in the antenna due to this motion?
38. The rectangular loop of N turns shown below moves to the right with a constant velocity →v while leaving the poles of a large electromagnet. (a) Assuming that the magnetic field is uniform between the pole faces and negligible elsewhere, determine the induced emf in the loop. (b) What is the source of work that produces this emf?
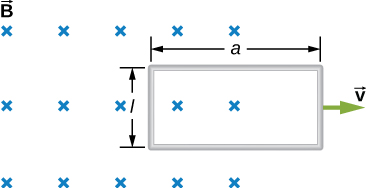
39. Suppose the magnetic field of the preceding problem oscillates with time according to B=B0sinωt. What then is the emf induced in the loop when its trailing side is a distance d from the right edge of the magnetic field region?
40. A coil of 1000 turns encloses an area of25cm2. It is rotated in 0.010 s from a position where its plane is perpendicular to Earth’s magnetic field to one where its plane is parallel to the field. If the strength of the field is 6.0×10−5T, what is the average emf induced in the coil?
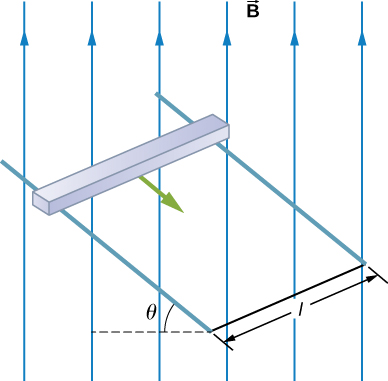
41. In the circuit shown in the accompanying figure, the rod slides along the conducting rails at a constant velocity →v. The velocity is in the same plane as the rails and directed at an angle θθ to them. A uniform magnetic field →B is directed out of the page. What is the emf induced in the rod?
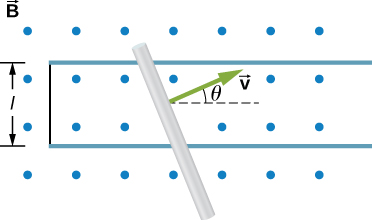
42. The rod shown in the accompanying figure is moving through a uniform magnetic field of strength B=0.50T with a constant velocity of magnitude v=8.0m/s.. What is the potential difference between the ends of the rod? Which end of the rod is at a higher potential?
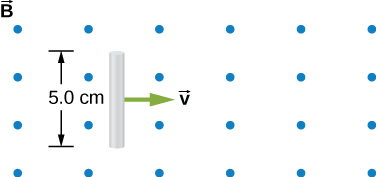
43. A 25-cm rod moves at 5.0 m/s in a plane perpendicular to a magnetic field of strength 0.25 T. The rod, velocity vector, and magnetic field vector are mutually perpendicular, as indicated in the accompanying figure. Calculate
(a) the magnetic force on an electron in the rod,
(b) the electric field in the rod, and
(c) the potential difference between the ends of the rod.
(d) What is the speed of the rod if the potential difference is 1.0 V?
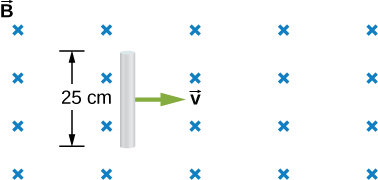
44. In the accompanying figure, the rails, connecting end piece, and rod all have a resistance per unit length of 2.0Ω/cm. The rod moves to the left at v=3.0m/s. If B=0.75T everywhere in the region, what is the current in the circuit
(a) when a=8.0cm?
(b) when a=5.0cm? Specify also the sense of the current flow.
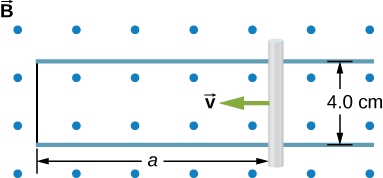
45. The rod shown below moves to the right on essentially zero-resistance rails at a speed of v=3.0m/s. If B=0.75T everywhere in the region, what is the current through the 5.0-Ω resistor? Does the current circulate clockwise or counterclockwise?
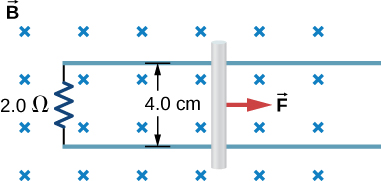
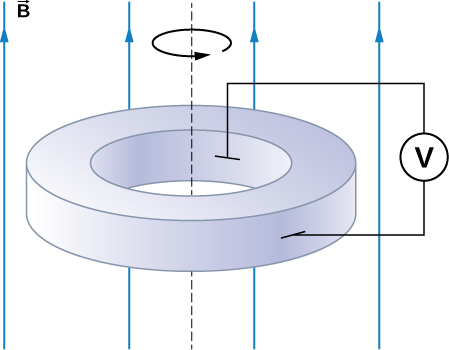
46. Shown below is a conducting rod that slides along metal rails. The apparatus is in a uniform magnetic field of strength 0.25 T, which is directly into the page. The rod is pulled to the right at a constant speed of 5.0 m/s by a force →F. The only significant resistance in the circuit comes from the 2.0-Ω resistor shown.
(a) What is the emf induced in the circuit?
(b) What is the induced current? Does it circulate clockwise or counter clockwise?
(c) What is the magnitude of →F?
(d) What are the power output of →F and the power dissipated in the resistor?
13.5 Induced Electric Fields
47. Calculate the induced electric field in a 50-turn coil with a diameter of 15 cm that is placed in a spatially uniform magnetic field of magnitude 0.50 T so that the face of the coil and the magnetic field are perpendicular. This magnetic field is reduced to zero in 0.10 seconds. Assume that the magnetic field is cylindrically symmetric with respect to the central axis of the coil.
48. The magnetic field through a circular loop of radius 10.0 cm varies with time as shown in the accompanying figure. The field is perpendicular to the loop. Assuming cylindrical symmetry with respect to the central axis of the loop, plot the induced electric field in the loop as a function of time.
49. The current I through a long solenoid with n turns per meter and radius R is changing with time as given by dI/dt. Calculate the induced electric field as a function of distance r from the central axis of the solenoid.
50. Calculate the electric field induced both inside and outside the solenoid of the preceding problem if I=I0sinωt..
51. Over a region of radius R, there is a spatially uniform magnetic field →B. (See below.) At t=0, B=1.0T, after which it decreases at a constant rate to zero in 30 s.
(a) What is the electric field in the regions where r≤R and r≥R during that 30-s interval?
(b) Assume that R=10.0cm. How much work is done by the electric field on a proton that is carried once clock wise around a circular path of radius 5.0 cm?
(c) How much work is done by the electric field on a proton that is carried once counterclockwise around a circular path of any radius r≥R?
(d) At the instant when B=0.50T, a proton enters the magnetic field at A, moving a velocity →v(v=5.0×106m/s) as shown. What are the electric and magnetic forces on the proton at that instant?
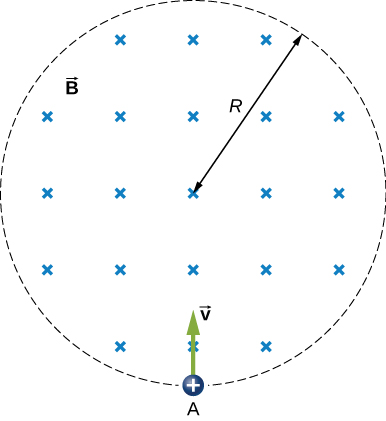
52. The magnetic field at all points within the cylindrical region whose cross-section is indicated in the accompanying figure starts at 1.0 T and decreases uniformly to zero in 20 s. What is the electric field (both magnitude and direction) as a function of r, the distance from the geometric center of the region?
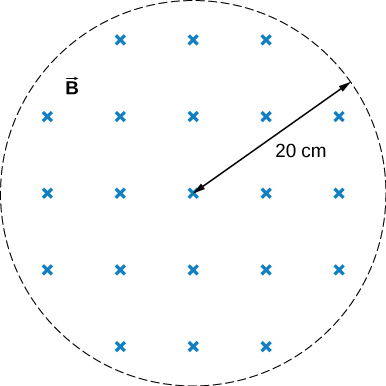
53. The current in a long solenoid of radius 3 cm is varied with time at a rate of 2 A/s. A circular loop of wire of radius 5 cm and resistance 2Ω surrounds the solenoid. Find the electrical current induced in the loop.
54. The current in a long solenoid of radius 3 cm and 20 turns/cm is varied with time at a rate of 2 A/s. Find the electric field at a distance of 4 cm from the center of the solenoid.
13.7 Electric Generators and Back Emf
55. Design a current loop that, when rotated in a uniform magnetic field of strength 0.10 T, will produce an emf ε=ε0sinωt,, where ε0=110V and ω=120πrad/s.
56. A flat, square coil of 20 turns that has sides of length 15.0 cm is rotating in a magnetic field of strength 0.050 T. If the maximum emf produced in the coil is 30.0 mV, what is the angular velocity of the coil?
57. A 50-turn rectangular coil with dimensions 0.15m×0.40m rotates in a uniform magnetic field of magnitude 0.75 T at 3600 rev/min.
(a) Determine the emf induced in the coil as a function of time.
(b) If the coil is connected to a 1000-Ω resistor, what is the power as a function of time required to keep the coil turning at 3600 rpm?
(c) Answer part (b) if the coil is connected to a 2000-Ω resistor.
58. The square armature coil of an alternating current generator has 200 turns and is 20.0 cm on side. When it rotates at 3600 rpm, its peak output voltage is 120 V.
(a) What is the frequency of the output voltage?
(b) What is the strength of the magnetic field in which the coil is turning?
59. A flip coil is a relatively simple device used to measure a magnetic field. It consists of a circular coil of N turns wound with fine conducting wire. The coil is attached to a ballistic galvanometer, a device that measures the total charge that passes through it. The coil is placed in a magnetic field →B such that its face is perpendicular to the field. It is then flipped through 180°,180°, and the total chargeQ that flows through the galvanometer is measured.
(a) If the total resistance of the coil and galvanometer is R, what is the relationship between B and Q? Because the coil is very small, you can assume that→B is uniform over it.
(b) How can you determine whether or not the magnetic field is perpendicular to the face of the coil?
60. The flip coil of the preceding problem has a radius of 3.0 cm and is wound with 40 turns of copper wire. The total resistance of the coil and ballistic galvanometer is 0.20Ω. When the coil is flipped through 180° in a magnetic field →B, a change of 0.090 C flows through the ballistic galvanometer.
(a) Assuming that →B and the face of the coil are initially perpendicular, what is the magnetic field?
(b) If the coil is flipped through 90°, what is the reading of the galvanometer?
61. A 120-V, series-wound motor has a field resistance of 80 Ω and an armature resistance of 10 Ω. When it is operating at full speed, a back emf of 75 V is generated.
(a) What is the initial current drawn by the motor? When the motor is operating at full speed, where are
(b) the current drawn by the motor,
(c) the power output of the source,
(d) the power output of the motor, and
(e) the power dissipated in the two resistances?
62. A small series-wound dc motor is operated from a 12-V car battery. Under a normal load, the motor draws 4.0 A, and when the armature is clamped so that it cannot turn, the motor draws 24 A. What is the back emf when the motor is operating normally?
Additional Problems
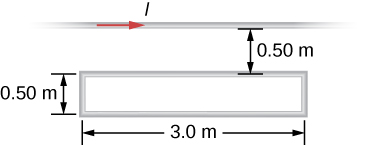
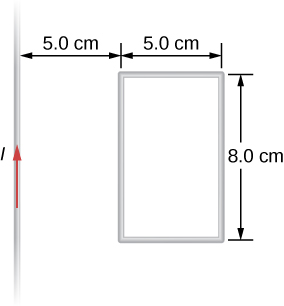
63. Shown in the following figure is a long, straight wire and a single-turn rectangular loop, both of which lie in the plane of the page. The wire is parallel to the long sides of the loop and is 0.50 m away from the closer side. At an instant when the emf induced in the loop is 2.0 V, what is the time rate of change of the current in the wire?
64. A metal bar of mass 500 g slides outward at a constant speed of 1.5 cm/s over two parallel rails separated by a distance of 30 cm which are part of a U-shaped conductor. There is a uniform magnetic field of magnitude 2 T pointing out of the page over the entire area. The railings and metal bar have an equivalent resistance of 150Ω.
(a) Determine the induced current, both magnitude and direction.
(b) Find the direction of the induced current if the magnetic field is pointing into the page.
(c) Find the direction of the induced current if the magnetic field is pointed into the page and the bar moves inwards.
65. A current is induced in a circular loop of radius 1.5 cm between two poles of a horseshoe electromagnet when the current in the electromagnet is varied. The magnetic field in the area of the loop is perpendicular to the area and has a uniform magnitude. If the rate of change of magnetic field is 10 T/s, find the magnitude and direction of the induced current if resistance of the loop is 25Ω.
66. A metal bar of length 25 cm is placed perpendicular to a uniform magnetic field of strength 3 T.
(a) Determine the induced emf between the ends of the rod when it is not moving.
(b) Determine the emf when the rod is moving perpendicular to its length and magnetic field with a speed of 50 cm/s.
67. A coil with 50 turns and area 10 cm2 is oriented with its plane perpendicular to a 0.75-T magnetic field. If the coil is flipped over (rotated through 180°) in 0.20 s, what is the average emf induced in it?
68. A 2-turn planer loop of flexible wire is placed inside a long solenoid of n turns per meter that carries a constant current I0. The areaA of the loop is changed by pulling on its sides while ensuring that the plane of the loop always remains perpendicular to the axis of the solenoid. If n=500turns per meter, I0=20A, and A=20cm2, what is the emf induced in the loop when dA/dt=100?
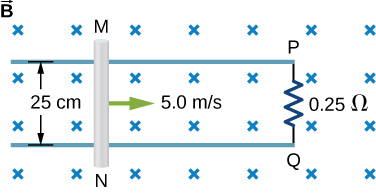
69. The conducting rod shown in the accompanying figure moves along parallel metal rails that are 25-cm apart. The system is in a uniform magnetic field of strength 0.75 T, which is directed into the page. The resistances of the rod and the rails are negligible, but the section PQ has a resistance of 0.25Ω.
(a) What is the emf (including its sense) induced in the rod when it is moving to the right with a speed of 5.0 m/s?
(b) What force is required to keep the rod moving at this speed?
(c) What is the rate at which work is done by this force?
(d) What is the power dissipated in the resistor?
70. A circular loop of wire of radius 10 cm is mounted on a vertical shaft and rotated at a frequency of 5 cycles per second in a region of uniform magnetic field of 2 Gauss perpendicular to the axis of rotation.
(a) Find an expression for the time-dependent flux through the ring.
(b) Determine the time-dependent current through the ring if it has a resistance of 10 Ω.
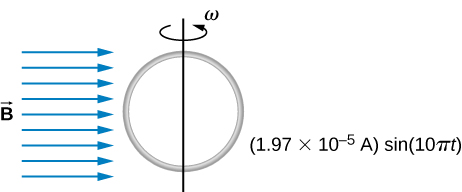
71. The magnetic field between the poles of a horseshoe electromagnet is uniform and has a cylindrical symmetry about an axis from the middle of the South Pole to the middle of the North Pole. The magnitude of the magnetic field changes as a rate of dB/dt due to the changing current through the electromagnet. Determine the electric field at a distance r from the center.
72. A long solenoid of radius a with n turns per unit length is carrying a time-dependent current I(t)=I0sin(ωt), where I0 and ω are constants. The solenoid is surrounded by a wire of resistance R that has two circular loops of radius b with b>a (see the following figure). Find the magnitude and direction of current induced in the outer loops at time t=0.
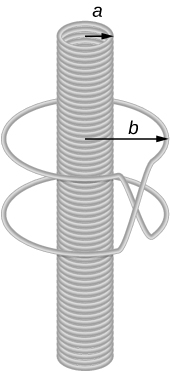
73. A 120-V, series-wound dc motor draws 0.50 A from its power source when operating at full speed, and it draws 2.0 A when it starts. The resistance of the armature coils is 10Ω.
(a) What is the resistance of the field coils?
(b) What is the back emf of the motor when it is running at full speed?
(c) The motor operates at a different speed and draws 1.0 A from the source. What is the back emf in this case?
74. The armature and field coils of a series-wound motor have a total resistance of 3.0Ω. When connected to a 120-V source and running at normal speed, the motor draws 4.0 A.
(a) How large is the back emf?
(b) What current will the motor draw just after it is turned on? Can you suggest a way to avoid this large initial current?
Challenge Problems
75. A copper wire of length L is fashioned into a circular coil with N turns. When the magnetic field through the coil changes with time, for what value of N is the induced emf a maximum?
76. A 0.50-kg copper sheet drops through a uniform horizontal magnetic field of 1.5 T, and it reaches a terminal velocity of 2.0 m/s.
(a) What is the net magnetic force on the sheet after it reaches terminal velocity?
(b) Describe the mechanism responsible for this force.
(c) How much power is dissipated as Joule heating while the sheet moves at terminal velocity?
77. A circular copper disk of radius 7.5 cm rotates at 2400 rpm around the axis through its center and perpendicular to its face. The disk is in a uniform magnetic field →B of strength 1.2 T that is directed along the axis. What is the potential difference between the rim and the axis of the disk?
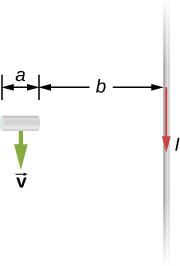
78. A short rod of length a moves with its velocity →v parallel to an infinite wire carrying a current I (see below). If the end of the rod nearer the wire is a distance b from the wire, what is the emf induced in the rod?
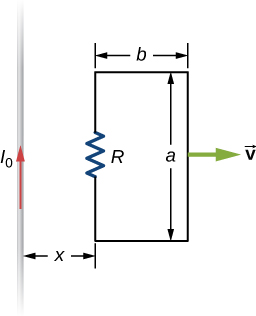
79. A rectangular circuit containing a resistance R is pulled at a constant velocity →v away from a long, straight wire carrying a current I0 (see below). Derive an equation that gives the current induced in the circuit as a function of the distance x between the near side of the circuit and the wire.
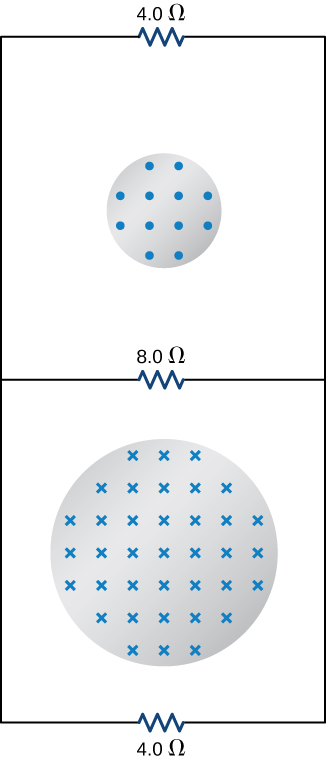
80. Two infinite solenoids cross the plane of the circuit as shown below. The radii of the solenoids are 0.10 and 0.20 m, respectively, and the current in each solenoid is changing such that dB/dt=50.0T/s. What are the currents in the resistors of the circuit?
81. An eight-turn coil is tightly wrapped around the outside of the long solenoid as shown below. The radius of the solenoid is 2.0 cm and it has 10 turns per centimeter. The current through the solenoid increases according to I=I0(1−e−αt), where I0=4.0A and α=2.0×10−2s−1. What is the emf induced in the coil when (a) t=0, (b) t=1.0×102s, and (c) t→∞?

82. Shown below is a long rectangular loop of width w, length l, mass m, and resistance R. The loop starts from rest at the edge of a uniform magnetic field →B and is pushed into the field by a constant force →F. Calculate the speed of the loop as a function of time.
83. A square bar of mass m and resistance R is sliding without friction down very long, parallel conducting rails of negligible resistance (see below). The two rails are a distance l apart and are connected to each other at the bottom of the incline by a zero-resistance wire. The rails are inclined at an angle θ, and there is a uniform vertical magnetic field →B throughout the region.
(a) Show that the bar acquires a terminal velocity given by v=mgRsinθB2l2cos2θ.
(b) Calculate the work per unit time done by the force of gravity.
(c) Compare this with the power dissipated in the Joule heating of the bar.
(d) What would happen if →B were reversed?
84. The accompanying figure shows a metal disk of inner radius r1 and other radius r2 rotating at an angular velocity →ω while in a uniform magnetic field directed parallel to the rotational axis. The brush leads of a voltmeter are connected to the dark’s inner and outer surfaces as shown. What is the reading of the voltmeter?
85. A long solenoid with 10 turns per centimeter is placed inside a copper ring such that both objects have the same central axis. The radius of the ring is 10.0 cm, and the radius of the solenoid is 5.0 cm.
(a) What is the emf induced in the ring when the current I through the solenoid is 5.0 A and changing at a rate of 100 A/s?
(b) What is the emf induced in the ring when I=2.0A and dI/dt=100A/s?
(c) What is the electric field inside the ring for these two cases?
(d) Suppose the ring is moved so that its central axis and the central axis of the solenoid are still parallel but no longer coincide. (You should assume that the solenoid is still inside the ring.) Now what is the emf induced in the ring?
(e) Can you calculate the electric field in the ring as you did in part (c)?
86. The current in the long, straight wire shown in the accompanying figure is given by I=I0sinωt, where I0=15A and ω=120πrad/s. What is the current induced in the rectangular loop at (a) t=0 and (b) t=2.1×10−3s? The resistance of the loop is 2.0Ω.
87. A 500-turn coil with a 0.250−m2 area is spun in Earth’s 5.00×10−5T magnetic field, producing a 12.0-kV maximum emf.
(a) At what angular velocity must the coil be spun?
(b) What is unreasonable about this result?
(c) Which assumption or premise is responsible?
88. A circular loop of wire of radius 10 cm is mounted on a vertical shaft and rotated at a frequency of 5 cycles per second in a region of uniform magnetic field of 2×10−4T perpendicular to the axis of rotation.
(a) Find an expression for the time-dependent flux through the ring
(b) Determine the time-dependent current through the ring if it has a resistance of 10Ω.
89. A long solenoid of radius aa with nn turns per unit length is carrying a time-dependent current I(t)=I0sinωt where I0 and ωω are constants. The solenoid is surrounded by a wire of resistance R that has two circular loops of radius b with b>a. Find the magnitude and direction of current induced in the outer loops at time t=0.
90. A rectangular copper loop of mass 100 g and resistance 0.2Ω is in a region of uniform magnetic field that is perpendicular to the area enclosed by the ring and horizontal to Earth’s surface (see below). The loop is let go from rest when it is at the edge of the nonzero magnetic field region.
(a) Find an expression for the speed when the loop just exits the region of uniform magnetic field.
(b) If it was let go at t=0t=0, what is the time when it exits the region of magnetic field for the following values: a=25cm,b=50cm,B=3T,g=9.8m/s2? Assume that the magnetic field of the induced current is negligible compared to 3 T.
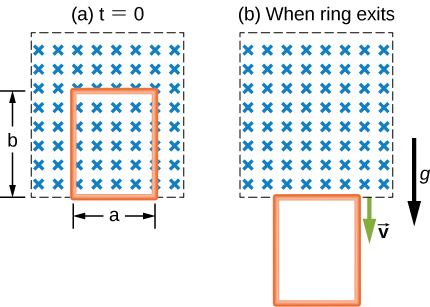
91. A metal bar of mass m slides without friction over two rails a distance D apart in the region that has a uniform magnetic field of magnitude B0 and direction perpendicular to the rails (see below). The two rails are connected at one end to a resistor whose resistance is much larger than the resistance of the rails and the bar. The bar is given an initial speed of v0. It is found to slow down. How far does the bar go before coming to rest? Assume that the magnetic field of the induced current is negligible compared to B0.
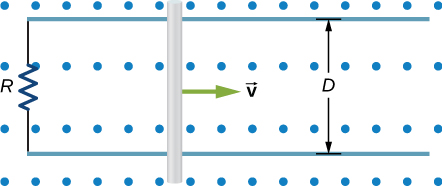
92. A time-dependent uniform magnetic field of magnitude B(t) is confined in a cylindrical region of radius R. A conducting rod of length 2D is placed in the region, as shown below. Show that the emf between the ends of the rod is given by dBdtD√R2−D2. (Hint: To find the emf between the ends, we need to integrate the electric field from one end to the other. To find the electric field, use Faraday’s law as “Ampère’s law for E.”)
Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), and Bill Moebs with many contributing authors. This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).


