13.6: Eddy Currents
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain how eddy currents are created in metals
- Describe situations where eddy currents are beneficial and where they are not helpful
As discussed two sections earlier, a motional emf is induced when a conductor moves in a magnetic field or when a magnetic field moves relative to a conductor. If motional emf can cause a current in the conductor, we refer to that current as an eddy current.
Magnetic Damping
Eddy currents can produce significant drag, called magnetic damping, on the motion involved. Consider the apparatus shown in Figure 13.6.1, which swings a pendulum bob between the poles of a strong magnet. (This is another favorite physics demonstration.) If the bob is metal, significant drag acts on the bob as it enters and leaves the field, quickly damping the motion. If, however, the bob is a slotted metal plate, as shown in part (b) of the figure, the magnet produces a much smaller effect. There is no discernible effect on a bob made of an insulator. Why does drag occur in both directions, and are there any uses for magnetic drag?
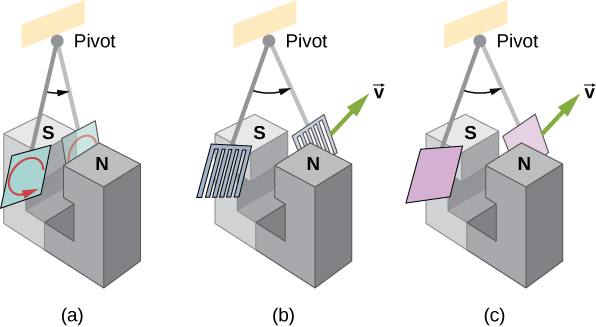
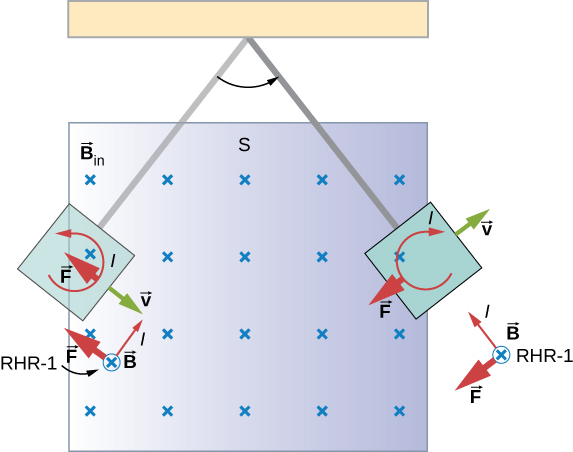
Figure 13.6.2 shows what happens to the metal plate as it enters and leaves the magnetic field. In both cases, it experiences a force opposing its motion. As it enters from the left, flux increases, setting up an eddy current (Faraday’s law) in the counterclockwise direction (Lenz’s law), as shown. Only the right-hand side of the current loop is in the field, so an unopposed force acts on it to the left (RHR-1). When the metal plate is completely inside the field, there is no eddy current if the field is uniform, since the flux remains constant in this region. But when the plate leaves the field on the right, flux decreases, causing an eddy current in the clockwise direction that, again, experiences a force to the left, further slowing the motion. A similar analysis of what happens when the plate swings from the right toward the left shows that its motion is also damped when entering and leaving the field.
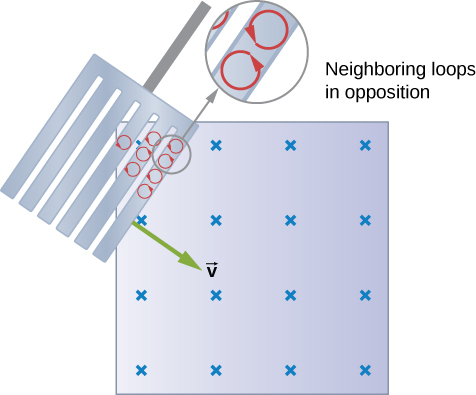
When a slotted metal plate enters the field (Figure 13.6.3), an emf is induced by the change in flux, but it is less effective because the slots limit the size of the current loops. Moreover, adjacent loops have currents in opposite directions, and their effects cancel. When an insulating material is used, the eddy current is extremely small, so magnetic damping on insulators is negligible. If eddy currents are to be avoided in conductors, then they must be slotted or constructed of thin layers of conducting material separated by insulating sheets.
Applications of Magnetic Damping
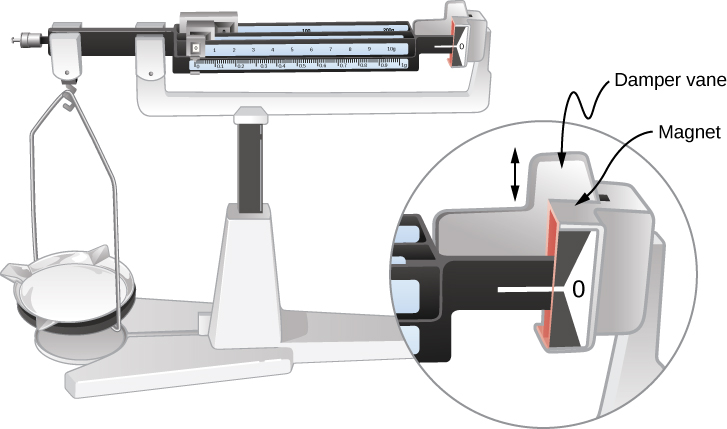
One use of magnetic damping is found in sensitive laboratory balances. To have maximum sensitivity and accuracy, the balance must be as friction-free as possible. But if it is friction-free, then it will oscillate for a very long time. Magnetic damping is a simple and ideal solution. With magnetic damping, drag is proportional to speed and becomes zero at zero velocity. Thus, the oscillations are quickly damped, after which the damping force disappears, allowing the balance to be very sensitive (Figure 13.6.4). In most balances, magnetic damping is accomplished with a conducting disc that rotates in a fixed field.
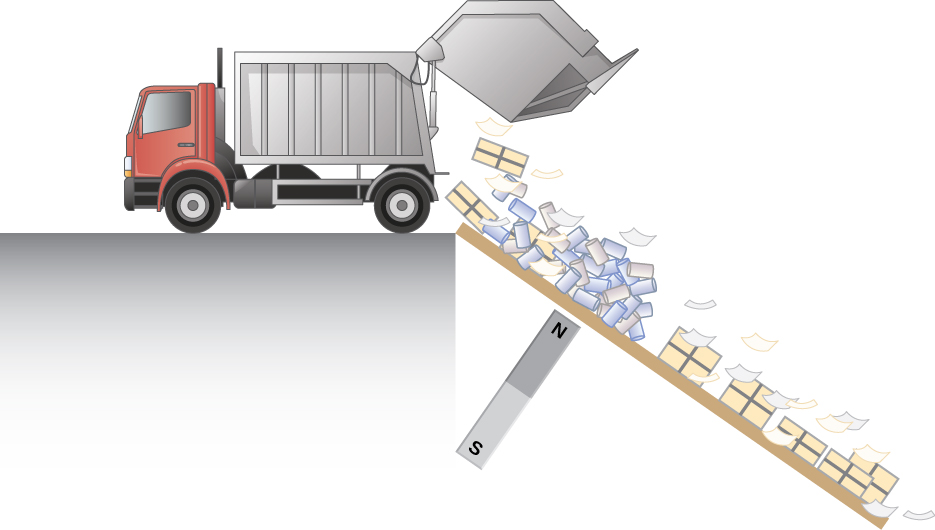
Since eddy currents and magnetic damping occur only in conductors, recycling centers can use magnets to separate metals from other materials. Trash is dumped in batches down a ramp, beneath which lies a powerful magnet. Conductors in the trash are slowed by magnetic damping while nonmetals in the trash move on, separating from the metals (Figure 13.6.5). This works for all metals, not just ferromagnetic ones. A magnet can separate out the ferromagnetic materials alone by acting on stationary trash.
Other major applications of eddy currents appear in metal detectors and braking systems in trains and roller coasters. Portable metal detectors (Figure 13.6.6) consist of a primary coil carrying an alternating current and a secondary coil in which a current is induced. An eddy current is induced in a piece of metal close to the detector, causing a change in the induced current within the secondary coil. This can trigger some sort of signal, such as a shrill noise.

Braking using eddy currents is safer because factors such as rain do not affect the braking and the braking is smoother. However, eddy currents cannot bring the motion to a complete stop, since the braking force produced decreases as speed is reduced. Thus, speed can be reduced from say 20 m/s to 5 m/s, but another form of braking is needed to completely stop the vehicle. Generally, powerful rare-earth magnets such as neodymium magnets are used in roller coasters. Figure 13.6.7 shows rows of magnets in such an application. The vehicle has metal fins (normally containing copper) that pass through the magnetic field, slowing the vehicle down in much the same way as with the pendulum bob shown in Figure 13.6.1.

Induction cooktops have electromagnets under their surface. The magnetic field is varied rapidly, producing eddy currents in the base of the pot, causing the pot and its contents to increase in temperature. Induction cooktops have high efficiencies and good response times but the base of the pot needs to be conductors, such as iron or steel, for induction to work.


