3.5: Examples

Example \(\PageIndex{1}\): Reading a Collision Graph

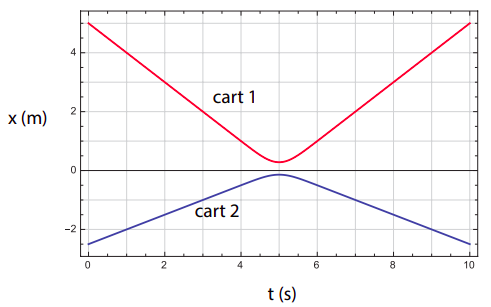
The graph shows a collision between two carts (possibly equipped with magnets so that they repel each other before they actually touch) on an air track. The inertia (mass) of cart 1 is 1 kg. Note: this is a position vs. time graph!

1. What are the initial velocities of the carts?
2. What are the final velocities of the carts?
3. What is the mass of the second cart?
4. Does the air track appear to be level? Why? (Hint: does the graph show any evidence of acceleration, for either cart, outside of the collision region?)
5. At the collision time, is the acceleration of the first cart positive or negative? How about the second cart? (Justify your answers.)
6. For the system consisting of the two carts, what is its initial (total) momentum? What is its final momentum?
7. Imagine now that one of the magnets is reversed, so when the carts collide they stick to each other. What would then be the final momentum of the system? What would be its final velocity?

Figure \(\PageIndex{1}\): A collision between two carts

Solution

(a) All the velocities are to be calculated by picking an easy straight part of each curve and calculating

\[ v=\frac{\Delta x}{\Delta t} \nonumber \]

for suitable intervals. In this way one gets

\begin{aligned}
&v_{1 i}=-1 \: \frac{\mathrm{m}}{\mathrm{s}}\\
&v_{2 i}=0.5 \: \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}

(b) Similarly, one gets

\begin{aligned}
&v_{1 f}=1 \: \frac{\mathrm{m}}{\mathrm{s}}\\
&v_{2 f}=-0.5 \: \frac{\mathrm{m}}{\mathrm{s}}
\end{aligned}

(c) Use this equation, or equivalent (conservation of momentum is OK)

\begin{aligned}
&\frac{m_{2}}{m_{1}}=-\frac{\Delta v_{1}}{\Delta v_{2}}\\
&\frac{m_{2}}{m_{1}}=-\frac{1-(-1)}{-0.5-0.5}=2
\end{aligned}

so the mass of the second cart is 2 kg.

(d) Yes, the track appears to be level because the carts do not show any evidence of acceleration outside of the collision region (the position vs. time curves are straight lines outside of the region approximately given by 4.5 s < \(t\) < 5.5 s).

(e) The acceleration of the first cart is positive. You can see this either graphically (the curve is like a parabola that opens upwards, i.e., concave), or algebraically (the cart’s velocity increases, going from −1 m/s to 1 m/s)

Similarly, the acceleration of the second cart is negative. The curve is like a parabola that opens downwards, i.e., convex; or, algebraically, the cart’s velocity decreases, going from 0.5 m/s to −0.5 m/s.

(f) The initial momentum of the system is

\[ p_{i}=m_{1} v_{1 i}+m_{2} v_{2 i}=(1 \: \mathrm{kg}) \times\left(-1 \: \frac{\mathrm{m}}{\mathrm{s}}\right)+(2 \: \mathrm{kg}) \times\left(0.5 \: \frac{\mathrm{m}}{\mathrm{s}}\right)=0 \nonumber \]

The final momentum is

\[ p_{f}=m_{1} v_{1 f}+m_{2} v_{2 f}=(1 \: \mathrm{kg}) \times\left(1 \: \frac{\mathrm{m}}{\mathrm{s}}\right)+(2 \: \mathrm{kg}) \times\left(-0.5 \: \frac{\mathrm{m}}{\mathrm{s}}\right)=0 \nonumber \]

You could also just say that the final momentum should be the same as the initial momentum, since the system appears to be isolated.

(g) The momentum should be conserved in this case as well, so \(p_f\) = 0. The velocity would be

\[ v_{f}=\frac{p_{f}}{m_{1}+m_{2}}=0 \nonumber .\]

Example \(\PageIndex{2}\): Collision in Different Reference Frames, Center of Mass, and Recoil

An 80-kg hockey player (call him player 1), moving at 3 m/s to the right, collides with a 90-kg player (player 2) who was moving at 2 m/s to the left. For a brief moment, they are stuck sliding together as they grab at each other.

1. What is their joint velocity as they slide together?
2. What was the velocity of their center of mass before and after the collision?
3. What does the collision look like to another player that was skating initially at 1.5 m/s to the right? Give all the initial and final velocities as seen by this player, and show explicitly that momentum is also conserved in this player’s frame of reference.
4. Eventually, the 90-kg player manages to push the other one back, in such a way that player 1 (the 80-kg player) ends up moving at 1 m/s to the left relative to player 2. What are their final velocities in the earth frame of reference?

Solution

(a) Call the initial velocities \(v_{1i}\) and \(v_{2i}\), the joint final velocity \(v_f\) , and assume the two players are an isolated system for practical purposes. Then conservation of momentum reads

\[ m_{1} v_{1 i}+m_{2} v_{2 i}=\left(m_{1}+m_{2}\right) v_{f} \label{eq:3.13} .\]

Solving for the final velocity, we get

\[ v_{f}=\frac{m_{1} v_{1 i}+m_{2} v_{2 i}}{m_{1}+m_{2}} \label{eq:3.14} .\]

Substituting the values given, we get

\[ v_{f}=\frac{80 \times 3-90 \times 2}{170}=0.353 \: \frac{\mathrm{m}}{\mathrm{s}} \label{eq:3.15} .\]

(b) According to Equation (3.3.3), the velocity of the center of mass, \(v_{cm}\), is just the same as what we just calculated (Equation \ref{eq:3.14}) above). This makes sense: after the collision, if the players are moving together, their system’s center of mass has to be moving with them. Also, if the system is isolated, the center of mass velocity should be the same before and after the collision. So the answer is \(v_{cm}\) = \(v_f\) = 0.353 m/s.

(c) Let me refer to this third player as “player 3,” and introduce a subscript “3” to refer to the quantities as seen in his frame of reference. Let also the subscript “\(E\)” denote the original, “Earth” reference frame. From Equation (1.3.6), we have then (for player 1, for instance)

\[ v_{31}=v_{3 E}+v_{E 1}=v_{E 1}-v_{E 3} \label{eq:3.16}\]

because \(v_{3E}\), the “velocity of the Earth in player 3’s reference frame,” is clearly equal to \(−v_{E3}\), the negative of the velocity of player 3 relative to the Earth. Basically, what Equation (\ref{eq:3.16}) is saying is that to convert all the Earth-frame velocities to the reference frame of player 3, we just need to subtract 1.5 m/s from them. This gives us

\[ \begin{align}
v_{31, i} &=3 \: \frac{\mathrm{m}}{\mathrm{s}}-1.5 \: \frac{\mathrm{m}}{\mathrm{s}}=1.5 \: \frac{\mathrm{m}}{\mathrm{s}} \nonumber \\
v_{32, i} &=-2 \: \frac{\mathrm{m}}{\mathrm{s}}-1.5 \: \frac{\mathrm{m}}{\mathrm{s}}=-3.5 \: \frac{\mathrm{m}}{\mathrm{s}} \nonumber \\
v_{31, f}=v_{32, f} &=0.353 \: \frac{\mathrm{m}}{\mathrm{s}}-1.5 \: \frac{\mathrm{m}}{\mathrm{s}}=-1.147 \: \frac{\mathrm{m}}{\mathrm{s}} \label{eq:3.17}
\end{align} \]

The total initial momentum in player’s 3 reference frame is then

\[ p_{s y s, i}=m_{1} v_{31, i}+m_{2} v_{32, i}=80 \times 1.5+90 \times(-3.5)=-195 \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}} \label{eq:3.18} \]

and the final momentum is

\[ p_{\text {sys }, f}=\left(m_{1}+m_{2}\right) v_{31, f}=170 \times(-1.147)=-195 \: \frac{\mathrm{kg} \cdot \mathrm{m}}{\mathrm{s}} \label{eq:3.19} .\]

So the total momentum is conserved in player 3’s reference frame. The reason for this is that this is an inertial reference frame, because the velocity of player 3 does not change.

(d) For this part of the problem, we are back to the original reference frame (the Earth reference frame), and we can drop the “\(E\)” subscript. For this new process, the final velocities from part (a) become the initial velocities, so we have \(v_{1i}\) = \(v_{2i}\) = 0.353 m/s. [Note: alternatively, since the system is isolated throughout, it would be OK in this case to use the velocities before the collision to calculate its total momentum, which also needs to be conserved in this process.] We are also told that the final velocity of player 1 relative to player 2 is \(v_{21,f}\) = \(v_{1f} − v_{2f}\) = −1 m/s. So we have two equations to solve:

\[ \begin{align}
\left(m_{1}+m_{2}\right) \times\left(0.353 \: \frac{\mathrm{m}}{\mathrm{s}}\right) &=m_{1} v_{1 f}+m_{2} v_{2 f} \quad \text { (conservation of momentum) } \nonumber \\
v_{1 f}-v_{2 f} &=-1 \: \frac{\mathrm{m}}{\mathrm{s}} \quad(\text { final relative velocity }) \label{eq:3.20}
\end{align} \]

Leaving aside the units for the moment, to make the equations more readable (the final units will work out, if we make sure to use SI units all along), we have:

\[ \begin{align}
(80+90) \times 0.353 &=80 v_{1 f}+90 v_{2 f} \\
v_{1 f} &=v_{2 f}-1 \label{eq:3.21}
\end{align} \]

Now substitute the second equation, which I have “solved” already for \(v_{1f}\) , in the first equation and solve for \(v_{2f}\) . The result is \(v_{2f}\) = 0.824 m/s, which, when substituted back in the relative velocity equation, gives \(v_{1f}\) = −0.176 m/s.