33: Particle Physics (Exercises)
- Page ID
- 4217
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conceptual Questions
33.3: Accelerators Create Matter from Energy
1. The total energy in the beam of an accelerator is far greater than the energy of the individual beam particles. Why isn’t this total energy available to create a single extremely massive particle?
2. Synchrotron radiation takes energy from an accelerator beam and is related to acceleration. Why would you expect the problem to be more severe for electron accelerators than proton accelerators?
3. What two major limitations prevent us from building high-energy accelerators that are physically small?
4. What are the advantages of colliding-beam accelerators? What are the disadvantages?
33.4: Particles, Patterns, and Conservation Laws
5. Large quantities of antimatter isolated from normal matter should behave exactly like normal matter. An antiatom, for example, composed of positrons, antiprotons, and antineutrons should have the same atomic spectrum as its matter counterpart. Would you be able to tell it is antimatter by its emission of antiphotons? Explain briefly.
6. Massless particles are not only neutral, they are chargeless (unlike the neutron). Why is this so?
7. Massless particles must travel at the speed of light, while others cannot reach this speed. Why are all massless particles stable? If evidence is found that neutrinos spontaneously decay into other particles, would this imply they have mass?
8. When a star erupts in a supernova explosion, huge numbers of electron neutrinos are formed in nuclear reactions. Such neutrinos from the 1987A supernova in the relatively nearby Magellanic Cloud were observed within hours of the initial brightening, indicating they traveled to earth at approximately the speed of light. Explain how this data can be used to set an upper limit on the mass of the neutrino, noting that if the mass is small the neutrinos could travel very close to the speed of light and have a reasonable energy (on the order of MeV).
9. Theorists have had spectacular success in predicting previously unknown particles. Considering past theoretical triumphs, why should we bother to perform experiments?
10. What lifetime do you expect for an antineutron isolated from normal matter?
11. Why does the \(\displaystyle η^0\) meson have such a short lifetime compared to most other mesons?
12. (a) Is a hadron always a baryon?
(b) Is a baryon always a hadron?
(c) Can an unstable baryon decay into a meson, leaving no other baryon?
13. Explain how conservation of baryon number is responsible for conservation of total atomic mass (total number of nucleons) in nuclear decay and reactions.
33.5: Quarks: Is That All There Is?
14. The quark flavor change \(\displaystyle d→u\) takes place in \(\displaystyle β^−\) decay. Does this mean that the reverse quark flavor change \(\displaystyle u→d\) takes place in \(\displaystyle β^+\) decay? Justify your response by writing the decay in terms of the quark constituents, noting that it looks as if a proton is converted into a neutron in β+ decay.
15. Explain how the weak force can change strangeness by changing quark flavor.
16. Beta decay is caused by the weak force, as are all reactions in which strangeness changes. Does this imply that the weak force can change quark flavor? Explain.
17. Why is it easier to see the properties of the c, b, and t quarks in mesons having composition \(\displaystyle W^−\) or \(\displaystyle t\bar{t}\) rather than in baryons having a mixture of quarks, such as \(\displaystyle udb\)?
18. How can quarks, which are fermions, combine to form bosons? Why must an even number combine to form a boson? Give one example by stating the quark substructure of a boson.
19. What evidence is cited to support the contention that the gluon force between quarks is greater than the strong nuclear force between hadrons? How is this related to color? Is it also related to quark confinement?
20. Discuss how we know that \(\displaystyle π-mesons (π^+,π,π^0)\) are not fundamental particles and are not the basic carriers of the strong force.
21. An antibaryon has three antiquarks with colors \(\displaystyle \bar{R}\bar{G}\bar{B}\). What is its color?
22. Suppose leptons are created in a reaction. Does this imply the weak force is acting? (for example, consider \(\displaystyle β\) decay.)
23. How can the lifetime of a particle indicate that its decay is caused by the strong nuclear force? How can a change in strangeness imply which force is responsible for a reaction? What does a change in quark flavor imply about the force that is responsible?
24. (a) Do all particles having strangeness also have at least one strange quark in them?
(b) Do all hadrons with a strange quark also have nonzero strangeness?
25. The sigma-zero particle decays mostly via the reaction \(\displaystyle \sum{}^0→Λ^0+γ\). Explain how this decay and the respective quark compositions imply that the \(\displaystyle \sum{}^0\) is an excited state of the \(\displaystyle Λ^0\).
26. What do the quark compositions and other quantum numbers imply about the relationships between the \(\displaystyle Δ^+\) and the proton? The \(\displaystyle Δ^0\) and the neutron?
27. Discuss the similarities and differences between the photon and the \(\displaystyle Z^0\) in terms of particle properties, including forces felt.
28. Identify evidence for electroweak unification.
29. The quarks in a particle are confined, meaning individual quarks cannot be directly observed. Are gluons confined as well? Explain
33.6: Grand Unified Theories
30. If a GUT is proven, and the four forces are unified, it will still be correct to say that the orbit of the moon is determined by the gravitational force. Explain why.
31. If the Higgs boson is discovered and found to have mass, will it be considered the ultimate carrier of the weak force? Explain your response.
32. Gluons and the photon are massless. Does this imply that the \(\displaystyle W^+, W^−\), and \(\displaystyle Z^0\) are the ultimate carriers of the weak force?
Problems & Exercises
33.1: The Yukawa Particle and the Heisenberg Uncertainty Principle Revisited
33. A virtual particle having an approximate mass of \(\displaystyle 10^{14}GeV/c^2\) may be associated with the unification of the strong and electroweak forces. For what length of time could this virtual particle exist (in temporary violation of the conservation of mass-energy as allowed by the Heisenberg uncertainty principle)?
Solution
\(\displaystyle 3×10^{−39}s\)
34. Calculate the mass in \(\displaystyle GeV/c^2\) of a virtual carrier particle that has a range limited to \(\displaystyle 10^{−30}\) m by the Heisenberg uncertainty principle. Such a particle might be involved in the unification of the strong and electroweak forces.
35. Another component of the strong nuclear force is transmitted by the exchange of virtual K-mesons. Taking K-mesons to have an average mass of \(\displaystyle 495MeV/c^2\), what is the approximate range of this component of the strong force?
Solution
\(\displaystyle 1.99×10^{−16}m(0.2fm)\)
33.2: The Four Basic Forces
36. (a) Find the ratio of the strengths of the weak and electromagnetic forces under ordinary circumstances.
(b) What does that ratio become under circumstances in which the forces are unified?
Solution
(a) \(\displaystyle 10^{−11}\) to 1, weak to EM
(b) 1 to 1
37. The ratio of the strong to the weak force and the ratio of the strong force to the electromagnetic force become 1 under circumstances where they are unified. What are the ratios of the strong force to those two forces under normal circumstances?
33.3: Accelerators Create Matter from Energy
38. At full energy, protons in the 2.00-km-diameter Fermilab synchrotron travel at nearly the speed of light, since their energy is about 1000 times their rest mass energy.
(a) How long does it take for a proton to complete one trip around?
(b) How many times per second will it pass through the target area?
Solution
(a) \(\displaystyle 2.09×10^{−5}s\)
(b) \(\displaystyle 4.77×10^4Hz\)
39. Suppose a \(\displaystyle W^−\) created in a bubble chamber lives for \(\displaystyle 5.00×10^{−25}s\). What distance does it move in this time if it is traveling at 0.900 c? Since this distance is too short to make a track, the presence of the \(\displaystyle W^−\) must be inferred from its decay products. Note that the time is longer than the given \(\displaystyle W^−\) lifetime, which can be due to the statistical nature of decay or time dilation.
40. What length track does a \(\displaystyle π^+\) traveling at 0.100 c leave in a bubble chamber if it is created there and lives for \(\displaystyle 2.60×10^{−8}s\)? (Those moving faster or living longer may escape the detector before decaying.)
Solution
78.0 cm
41. The 3.20-km-long SLAC produces a beam of 50.0-GeV electrons. If there are 15,000 accelerating tubes, what average voltage must be across the gaps between them to achieve this energy?
42. Because of energy loss due to synchrotron radiation in the LHC at CERN, only 5.00 MeV is added to the energy of each proton during each revolution around the main ring. How many revolutions are needed to produce 7.00-TeV (7000 GeV) protons, if they are injected with an initial energy of 8.00 GeV?
Solution
\(\displaystyle 1.40×10^6\)
43. A proton and an antiproton collide head-on, with each having a kinetic energy of 7.00 TeV (such as in the LHC at CERN). How much collision energy is available, taking into account the annihilation of the two masses? (Note that this is not significantly greater than the extremely relativistic kinetic energy.)
44. When an electron and positron collide at the SLAC facility, they each have 50.0 GeV kinetic energies. What is the total collision energy available, taking into account the annihilation energy? Note that the annihilation energy is insignificant, because the electrons are highly relativistic.
Solution
100 GeV
33.4: Particles, Patterns, and Conservation Laws
45. The π0 is its own antiparticle and decays in the following manner: \(\displaystyle π^0→γ+γ\). What is the energy of each \(\displaystyle γ\) ray if the \(\displaystyle π^0\) is at rest when it decays?
Solution
67.5 MeV
46. The primary decay mode for the negative pion is \(\displaystyle π^−→μ^−+\bar{ν_μ}\). What is the energy release in MeV in this decay?
47. The mass of a theoretical particle that may be associated with the unification of the electroweak and strong forces is 1014GeV/c2.
(a) How many proton masses is this?
(b) How many electron masses is this? (This indicates how extremely relativistic the accelerator would have to be in order to make the particle, and how large the relativistic quantity \(\displaystyle γ\) would have to be.)
Solution
(a) \(\displaystyle 1×10^{14}\)
(b) \(\displaystyle 2×10^{17}\)
48. The decay mode of the negative muon is \(\displaystyle μ^−→e^−+\bar{ν_e}+ν_μ\).
(a) Find the energy released in MeV.
(b) Verify that charge and lepton family numbers are conserved.
49. The decay mode of the positive tau is \(\displaystyle τ^+→μ^++ν_μ+\bar{ν_τ}\).
(a) What energy is released?
(b) Verify that charge and lepton family numbers are conserved.
(c) The \(\displaystyle τ^+\) is the antiparticle of the \(\displaystyle τ^−\).Verify that all the decay products of the \(\displaystyle τ^+\) are the antiparticles of those in the decay of the \(\displaystyle τ^−\) given in the text.
Solution
(a) 1671 MeV
(b) \(\displaystyle Q=1,Q'=1+0+0=1.L_τ=−1;L'τ=−1;Lμ=0;L'μ=−1+1=0\)
(c) \(\displaystyle τ^−→μ^−+v_μ+\bar{v_τ}⇒μ^−\) antiparticle of \(\displaystyle μ^+; v_μ\) of \(\displaystyle \bar{v_μ}; \bar{v_τ}\) of \(\displaystyle v_τ\)
50. The principal decay mode of the sigma zero is \(\displaystyle \sum{}^0→Λ^0+γ\).
(a) What energy is released?
(b) Considering the quark structure of the two baryons, does it appear that the \(\displaystyle \sum{}^0\) is an excited state of the \(\displaystyle Λ^0\)?
(c) Verify that strangeness, charge, and baryon number are conserved in the decay.
(d) Considering the preceding and the short lifetime, can the weak force be responsible? State why or why not.
51. (a) What is the uncertainty in the energy released in the decay of a \(\displaystyle π^0\) due to its short lifetime?
(b) What fraction of the decay energy is this, noting that the decay mode is \(\displaystyle π^0→γ+γ\) (so that all the \(\displaystyle π^0\) mass is destroyed)?
Solution
(a) 3.9 eV
(b) \(\displaystyle 2.9×10^{−8}\)
52. (a) What is the uncertainty in the energy released in the decay of a \(\displaystyle τ^−\) due to its short lifetime?
(b) Is the uncertainty in this energy greater than or less than the uncertainty in the mass of the tau neutrino? Discuss the source of the uncertainty.
33.5: Quarks: Is That All There Is?
53. (a) Verify from its quark composition that the \(\displaystyle Δ^+\) particle could be an excited state of the proton.
(b) There is a spread of about 100 MeV in the decay energy of the \(\displaystyle Δ^+\), interpreted as uncertainty due to its short lifetime. What is its approximate lifetime?
(c) Does its decay proceed via the strong or weak force?
Solution
(a) The \(\displaystyle uud\) composition is the same as for a proton.
(b) \(\displaystyle 3.3×10^{−24}s\)
(c) Strong (short lifetime)
54. Accelerators such as the Triangle Universities Meson Facility (TRIUMF) in British Columbia produce secondary beams of pions by having an intense primary proton beam strike a target. Such “meson factories” have been used for many years to study the interaction of pions with nuclei and, hence, the strong nuclear force. One reaction that occurs is \(\displaystyle π^++p→Δ^{++}→π^++p\), where the \(\displaystyle Δ^{++}\) is a very short-lived particle. The graph in Figure shows the probability of this reaction as a function of energy. The width of the bump is the uncertainty in energy due to the short lifetime of the \(\displaystyle Δ^{++}\).
(a) Find this lifetime.
(b) Verify from the quark composition of the particles that this reaction annihilates and then re-creates a \(\displaystyle d\) quark and a \(\displaystyle \bar{d}\) antiquark by writing the reaction and decay in terms of quarks.
(c) Draw a Feynman diagram of the production and decay of the \(\displaystyle Δ^{++}\) showing the individual quarks involved.
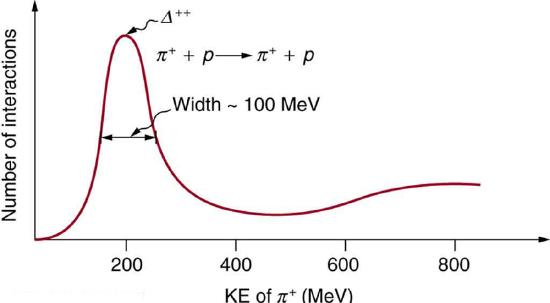
This graph shows the probability of an interaction between a \(\displaystyle π^+\) and a proton as a function of energy. The bump is interpreted as a very short lived particle called a \(\displaystyle Δ^{++}\). The approximately 100-MeV width of the bump is due to the short lifetime of the \(\displaystyle Δ^{++}\).
55. The reaction \(\displaystyle π^++p→Δ^{++}\) (described in the preceding problem) takes place via the strong force.
(a) What is the baryon number of the \(\displaystyle Δ^{++}\) particle?
(b) Draw a Feynman diagram of the reaction showing the individual quarks involved.
Solution
a) \(\displaystyle Δ^{++}(uuu);B=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1\)
b)
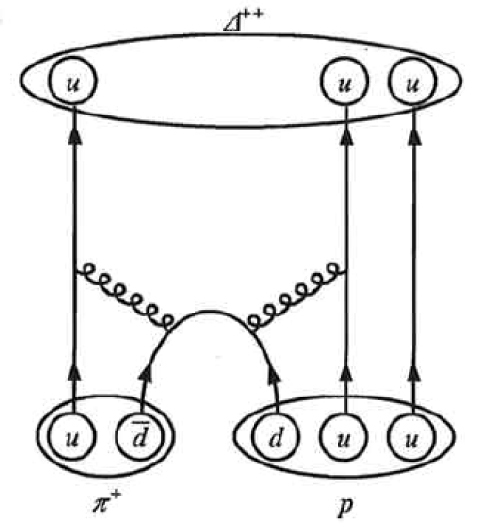
56. One of the decay modes of the omega minus is \(\displaystyle Ω^−→Ξ^0+π^−\).
(a) What is the change in strangeness?
(b) Verify that baryon number and charge are conserved, while lepton numbers are unaffected.
(c) Write the equation in terms of the constituent quarks, indicating that the weak force is responsible.
57. Repeat the previous problem for the decay mode \(\displaystyle Ω^−→Λ^0+K^−\).
Solution
(a) \(\displaystyle +1\)
(b) \(\displaystyle B=1=1+0, Z==0+(−1)\), all lepton numbers are 0 before and after
(c) \(\displaystyle (sss)→(uds)+(\bar{u}s)\)
58. One decay mode for the eta-zero meson is \(\displaystyle η^0→γ+γ\).
(a) Find the energy released.
(b) What is the uncertainty in the energy due to the short lifetime?
(c) Write the decay in terms of the constituent quarks.
(d) Verify that baryon number, lepton numbers, and charge are conserved.
59. One decay mode for the eta-zero meson is \(\displaystyle η^0→π^0+π^0\).
(a) Write the decay in terms of the quark constituents.
(b) How much energy is released?
(c) What is the ultimate release of energy, given the decay mode for the pi zero is π0→γ+γ?
Solution
(a) \(\displaystyle (u\bar{u}+d\bar{d})→(u\bar{u}+d\bar{d})+(u\bar{u}+d\bar{d})\)
(b) 277.9 MeV
(c) 547.9 MeV
60. Is the decay \(\displaystyle n→e^++e^−\) possible considering the appropriate conservation laws? State why or why not.
61. Is the decay \(\displaystyle μ^−→e^−+ν_e+ν_μ\) possible considering the appropriate conservation laws? State why or why not.
Solution
No. \(\displaystyle Charge=−1\) is conserved. \(\displaystyle L_{e_i}=0≠L_{e_f}=2\) is not conserved. \(\displaystyle L_μ=1\) is conserved.
62. (a) Is the decay \(\displaystyle Λ^0→n+π^0\) possible considering the appropriate conservation laws? State why or why not.
(b) Write the decay in terms of the quark constituents of the particles.
63. (a) Is the decay \(\displaystyle \sum{}^−→n+π^−\) possible considering the appropriate conservation laws? State why or why not. (b) Write the decay in terms of the quark constituents of the particles.
Solution
(a)Yes. \(\displaystyle Z=−1=0+(−1), B=1=1+0\), all lepton family numbers are 0 before and after, spontaneous since mass greater before reaction.
(b) \(\displaystyle dds→udd+\bar{u}d\)
64. The only combination of quark colors that produces a white baryon is RGB. Identify all the color combinations that can produce a white meson.
65. (a) Three quarks form a baryon. How many combinations of the six known quarks are there if all combinations are possible?
(b) This number is less than the number of known baryons. Explain why.
Solution
(a) 216
(b) There are more baryons observed because we have the 6 antiquarks and various mixtures of quarks (as for the π-meson) as well.
66. (a) Show that the conjectured decay of the proton, \(\displaystyle p→π^0+e^+\), violates conservation of baryon number and conservation of lepton number.
(b) What is the analogous decay process for the antiproton?
67. Verify the quantum numbers given for the \(\displaystyle Ω^+\) in [link] by adding the quantum numbers for its quark constituents as inferred from Table.
Solution
\(\displaystyle Ω+(\bar{s}\bar{s}\bar{s})\)
\(\displaystyle B=−\frac{1}{3}−\frac{1}{3}−\frac{1}{3}=−1,\)
\(\displaystyle L_e,μ,τ=0+0+0=0,\)
\(\displaystyle Q=\frac{1}{3}+\frac{1}{3}+\frac{1}{3}=1,\)
\(\displaystyle S=1+1+1=3.\)
68. Verify the quantum numbers given for the proton and neutron in [link] by adding the quantum numbers for their quark constituents as given in Table.
69. (a) How much energy would be released if the proton did decay via the conjectured reaction \(\displaystyle p→π^0+e^+\)?
(b) Given that the \(\displaystyle π^0\) decays to two \(\displaystyle γ\) s and that the \(\displaystyle e^+\) will find an electron to annihilate, what total energy is ultimately produced in proton decay?
(c) Why is this energy greater than the proton’s total mass (converted to energy)?
Solution
(a)803 MeV
(b) 938.8 MeV
(c) The annihilation energy of an extra electron is included in the total energy.
70. (a) Find the charge, baryon number, strangeness, charm, and bottomness of the \(\displaystyle J/Ψ\) particle from its quark composition.
(b) Do the same for the Υ particle.
71. There are particles called D-mesons. One of them is the \(\displaystyle D^+\) meson, which has a single positive charge and a baryon number of zero, also the value of its strangeness, topness, and bottomness. It has a charm of \(\displaystyle +1\). What is its quark configuration?
Solution
\(\displaystyle c\bar{d}\)
72. There are particles called bottom mesons or B-mesons. One of them is the \(\displaystyle B^−\) meson, which has a single negative charge; its baryon number is zero, as are its strangeness, charm, and topness. It has a bottomness of \(\displaystyle −1\). What is its quark configuration?
73. (a) What particle has the quark composition \(\displaystyle \bar{u}\bar{u}\bar{d}\)?
(b) What should its decay mode be?
Solution
a) The antiproton
b) \(\displaystyle p^−→π^0+e^−\)
74. (a) Show that all combinations of three quarks produce integral charges. Thus baryons must have integral charge.
(b) Show that all combinations of a quark and an antiquark produce only integral charges. Thus mesons must have integral charge.
33.6: Grand Unified Theories
75. Integrated Concepts
The intensity of cosmic ray radiation decreases rapidly with increasing energy, but there are occasionally extremely energetic cosmic rays that create a shower of radiation from all the particles they create by striking a nucleus in the atmosphere as seen in the figure given below. Suppose a cosmic ray particle having an energy of \(\displaystyle 10^{10}GeV\) converts its energy into particles with masses averaging \(\displaystyle 200MeV/c^2\).
(a) How many particles are created?
(b) If the particles rain down on a \(\displaystyle 1.00-km^2\) area, how many particles are there per square meter?
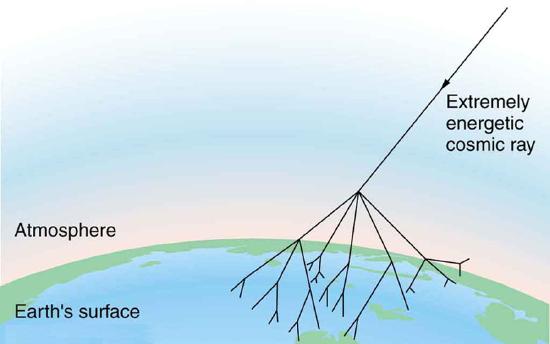
An extremely energetic cosmic ray creates a shower of particles on earth. The energy of these rare cosmic rays can approach a joule (about \(\displaystyle 10^{10}GeV\)) and, after multiple collisions, huge numbers of particles are created from this energy. Cosmic ray showers have been observed to extend over many square kilometers.
Solution
(a) \(\displaystyle 5×10^{10}\)
(b) \(\displaystyle 5×10^4particles/m^2\)
76. Integrated Concepts
Assuming conservation of momentum, what is the energy of each γ ray produced in the decay of a neutral at rest pion, in the reaction \(\displaystyle π^0→γ+γ\)?
77. Integrated Concepts
What is the wavelength of a 50-GeV electron, which is produced at SLAC? This provides an idea of the limit to the detail it can probe.
Solution
\(\displaystyle 2.5×10^{−17}m\)
78. Integrated Concepts
(a) Calculate the relativistic quantity \(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) for 1.00-TeV protons produced at Fermilab.
(b) If such a proton created a \(\displaystyle π^+\) having the same speed, how long would its life be in the laboratory?
(c) How far could it travel in this time?
79. Integrated Concepts
The primary decay mode for the negative pion is \(\displaystyle π^−→μ^−+\bar{ν_μ}\).
(a) What is the energy release in MeV in this decay?
(b) Using conservation of momentum, how much energy does each of the decay products receive, given the \(\displaystyle π^−\) is at rest when it decays? You may assume the muon antineutrino is massless and has momentum \(\displaystyle p=E/c\), just like a photon.
Solution
(a) 33.9 MeV
(b) Muon antineutrino 29.8 MeV, muon 4.1 MeV (kinetic energy)
80. Integrated Concepts
Plans for an accelerator that produces a secondary beam of K-mesons to scatter from nuclei, for the purpose of studying the strong force, call for them to have a kinetic energy of 500 MeV.
(a) What would the relativistic quantity \(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) be for these particles?
(b) How long would their average lifetime be in the laboratory?
(c) How far could they travel in this time?
81. Integrated Concepts
Suppose you are designing a proton decay experiment and you can detect 50 percent of the proton decays in a tank of water.
(a) How many kilograms of water would you need to see one decay per month, assuming a lifetime of \(\displaystyle 10^{31}y\)?
(b) How many cubic meters of water is this?
(c) If the actual lifetime is \(\displaystyle 10^{33}y\), how long would you have to wait on an average to see a single proton decay?
Solution
(a) \(\displaystyle 7.2×10^5kg\)
(b) \(\displaystyle 7.2×10^2m^3\)
(c) 100 months
82. Integrated Concepts
In supernovas, neutrinos are produced in huge amounts. They were detected from the 1987A supernova in the Magellanic Cloud, which is about 120,000 light years away from the Earth (relatively close to our Milky Way galaxy). If neutrinos have a mass, they cannot travel at the speed of light, but if their mass is small, they can get close.
(a) Suppose a neutrino with a \(\displaystyle 7-eV/c^2\) mass has a kinetic energy of 700 keV. Find the relativistic quantity \(\displaystyle γ=\frac{1}{\sqrt{1−v^2/c^2}}\) for it.
(b) If the neutrino leaves the 1987A supernova at the same time as a photon and both travel to Earth, how much sooner does the photon arrive? This is not a large time difference, given that it is impossible to know which neutrino left with which photon and the poor efficiency of the neutrino detectors. Thus, the fact that neutrinos were observed within hours of the brightening of the supernova only places an upper limit on the neutrino’s mass. (Hint: You may need to use a series expansion to find v for the neutrino, since its γ is so large.)
83. Construct Your Own Problem
Consider an ultrahigh-energy cosmic ray entering the Earth’s atmosphere (some have energies approaching a joule). Construct a problem in which you calculate the energy of the particle based on the number of particles in an observed cosmic ray shower. Among the things to consider are the average mass of the shower particles, the average number per square meter, and the extent (number of square meters covered) of the shower. Express the energy in eV and joules.
84. Construct Your Own Problem
Consider a detector needed to observe the proposed, but extremely rare, decay of an electron. Construct a problem in which you calculate the amount of matter needed in the detector to be able to observe the decay, assuming that it has a signature that is clearly identifiable. Among the things to consider are the estimated half life (long for rare events), and the number of decays per unit time that you wish to observe, as well as the number of electrons in the detector substance.
Contributors and Attributions
Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).

