9.2: The Wave Equation
- Page ID
- 17418
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)As with all phenomena in classical mechanics, the motion of the particles in a wave, for instance the masses on springs in Figure 9.1.1, are governed by Newton’s laws of motion and the various force laws. In this section we will use these laws to derive an equation of motion for the wave itself, which applies quite generally to wave phenomena. To do so, consider a series of particles of equal mass \(m\) connected by springs of spring constant \(k\), again as in Figure 9.1.1a, and assume that at rest the distance between any two masses is h. Let the position of particle \(i\) be \(x\), and \(u\) the distance that particle is away from its rest position; then \(u=x_{\text {rest }}-x\) is a function of both position \(x\) and time \(t\). Suppose particle \(i\) has moved to the left, then it will feel a restoring force to the right due to two sources: the compressed spring on its left, and the extended spring on its right.The total force to the right is then given by:
\[\begin{align} F_{i} &=F_{i+1 \rightarrow i}-F_{i-1 \rightarrow i} \\ &=k[u(x+h, t)-u(x, t)]-k[u(x, t)-u(x-h, t)] \\ &=k[u(x+h, t)-2 u(x, t)+u(x-h, t)] \label{9.3} \end{align}\]
Equation \ref{9.3} gives the net force on particle \(i\), which by Newton’s second law of motion (Equation 2.1.5) equals the particle’s mass times its acceleration. The acceleration is the second time derivative of the position \(x\),but since the equilibrium position is a constant, it is also the second time derivative of the distance from the equilibrium position \(u(x,t)\), and we have:
\[F_{\mathrm{net}}=m \frac{\partial^{2} u(x, t)}{\partial t^{2}}=k[u(x+h, t)-2 u(x, t)+u(x-h, t)] \label{9.4}\]
Equation \ref{9.4} holds for particle \(i\), but just as well for particle \(i+1\), or \(i-10\). We can get an equation for \(N\) particles by simply adding their individual equations, which we can do because these equations are linear.We thus find for a string of particles of length \(L=Nh\) hand total mass \(M=N m\):
\[\frac{\partial^{2} u(x, t)}{\partial t^{2}}=\frac{K L^{2}}{M} \frac{u(x+h, t)-2 u(x, t)+u(x-h, t)}{h^{2}} \label{9.5}.\]
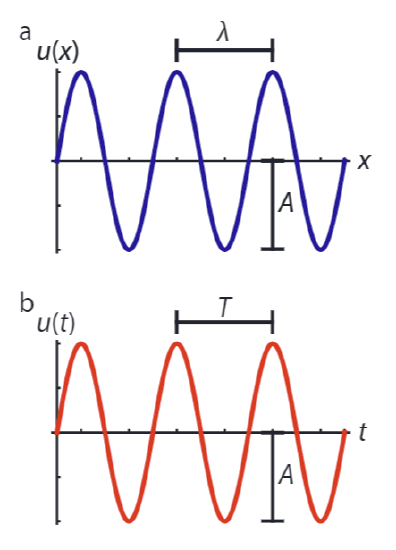
Here \(K = k/N\) is the effective spring constant of the N springs in series. Now take a close look at the fraction on the right hand side of Equation \ref{9.5}: if we take the limit \(h \rightarrow 0\), this is the second derivative of \(u(x,t)\) with respect to x. However, taking \(h\) to zero also takes \(L\) to zero - which we can counteract by simultaneously taking \(N \rightarrow \infty\), in such a way that their product L remains the same. What we end up with is a string of infinitely many particles connected by infinitely many springs - so a continuum of particles and springs, for which the equation of motion is given by the wave equation:
\[\frac{\partial^{2} u(x, t)}{\partial t^{2}}=v_{\mathrm{w}}^{2} \frac{\partial^{2} u(x, t)}{\partial x^{2}} \label{9.6}\]
In Equation \ref{9.6}, \(v_{\mathrm{w}}=\sqrt{\frac{K L^{2}}{M}}\) (sometimes also denoted by c) is the wave speed.
For a wave in a taut string, the one-dimensional description is accurate, and we can relate our quantities \(K, L\) and \(M\) to more familiar properties of the string: its tension \(T = KL\) with the dimension of a force (this is simply Hooke’s law again) and its mass per unit length \(\mu = \frac{M}{L}\), so we get
\[v_{\mathrm{string}}=\sqrt{\frac{T}{\mu}}\]
In two or three dimensions, the spatial derivative in Equation \ref{9.6} becomes a Laplacian operator, and the wave equation is given by:
\[\frac{\partial^{2} u(\boldsymbol{x}, t)}{\partial t^{2}}=v_{\mathrm{w}}^{2} \nabla^{2} u(\boldsymbol{x}, t) \label{9.8}\]
As can be readily seen by writing Equation \ref{9.8} in terms of spherical coordinates, if the wave is radial (i.e., only depends on the distance to the source \(r\), and not on the angle), the quantity \(ru(r)\) obeys the one-dimensional wave equation, so we can write down the equation for \(u(r)\) immediately. An important application are sound waves, which spread uniformly in a uniform medium. To find their speed, we characterize the medium in a similar fashion as we did for the string: we take the mass per unit volume, which is simply the density \(\rho\), and the medium’s bulk modulus, which is a measure for the medium’s resistance to compression (i.e., a kind of three-dimensional analog of the spring constant), defined as:
\[B=-V \frac{\mathrm{d} p}{\mathrm{d} V}=\rho \frac{\mathrm{d} p}{\mathrm{d} \rho}\]
where \(p\) is the pressure (force per unit area) and \(V\) the volume. The bulk modulus is also sometimes denoted as \(K\). The dimensions of the bulk modulus are those of a pressure, or force per unit area, and those of the density are mass per unit volume, so their ratio has the dimension of a speed squared, and the speed of sound is given by:
\[v_{\text {sound }}=\sqrt{\frac{B}{\rho}}\]
Equation \ref{9.8} describes a wave characterized by a one-dimensional displacement (either longitudinal or transverse) in three dimensions. In general a wave can have components of both, and the displacement itself becomes a vector quantity, \(\boldsymbol{u} (x,t)\). In that case the three-dimensional wave equation takes on a more complex form:
\[\rho \frac{\partial^{2} \boldsymbol{u}(\boldsymbol{x}, t)}{\partial t^{2}}=\boldsymbol{f}+\left(B+\frac{4}{3} G\right) \nabla(\nabla \cdot \boldsymbol{u}(\boldsymbol{x}, t))-G \nabla \times(\nabla \times \boldsymbol{u}(\boldsymbol{x}, t)) \label{9.11}\]
where \(\boldsymbol{f}\) is the driving force (per unit volume), \(B\) again the bulk modulus, and \(G\) the material’s shear modulus. Equation \ref{9.11} is used for the description of seismic waves in the Earth and the ultrasonic waves with which solid materials are probed for defects.


