15.8: Problems

Last updated
Save as PDF

Page ID: 33206

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Given a four-potential \(\underline{a}=(C y t,-C x t, 0,0)\) where \(C \) is a constant:
1. Determine whether this four-potential satisfies the Lorenz condition.
2. Compute the electric and magnetic fields from this four-potential.
Given \(\underline{a}_{1}=\left(C_{1} z t, 0,0, C_{2} x\right)\), find the electric and magnetic field components. Compare with the fields you get from \(\underline{a}_{2}=\left(C_{1} z t, C_{3} y,-C_{3} z, C_{2} x\right) . C_{1}, C_{2}, \text { and } C_{3}\) are constants. Can one have more than one four-potential field giving rise to the same electric and magnetic fields?
Suppose that in the rest frame we have a four-potential of the form \(\underline{a}=(0,0,0, K y)\) where \(K \) is a constant.
1. Find the electric and magnetic fields in this frame.
2. Find the components of \(a\) in a reference frame moving in the -\(x\) direction at speed \(U\). Hint: Draw a spacetime diagram showing the \(a\) vector and resolve into components in the moving frame using the spacetime Pythagorean theorem.
3. Find the electric and magnetic fields in the moving frame.
Assume a four-potential of the form \(\underline{a}=(\mathbf{A}, \phi / c), \text { where } \mathbf{A}=(K y, 0,0) \text { and } \phi=0\) in the rest frame, \(K \) being a constant.
1. Compute the electric and magnetic fields in the rest frame.
2. Find the components of the four-potential in a reference frame moving in the -\(x\) direction at speed \(U\).
3. Compute the electric and magnetic fields in the moving frame using the above results.
Using the right-hand rule, show that the electric torque acting on an electric dipole tries to align the dipole so that it is in its state of lowest potential energy.
The net electric force on an electric dipole is zero in a uniform electric field. However, if the field varies with position, this is not necessarily true. Consider an electric field that has the form \(\mathbf{E}=E_{0}(1+\alpha z) \mathbf{k}\) along the \(z\) axis, where \(E\) ₀ and \(α \) are positive constants.
1. An electric dipole consisting of charges ±\(q \) spaced by a distance \(d\) is centered at the origin. If the dipole is aligned with the electric field, determine the direction and magnitude of the net force on the dipole.
2. Determine the force on the dipole if it is anti-aligned with (i. e., pointing in the opposite direction from) the electric field.
Suppose that a charged particle is moving under the influence of electric and magnetic fields such that it periodically returns to some point P. If the four-potential is independent of time, will the kinetic energy of the particle be the same or different every time it returns to P? Explain.
Given constant electric and magnetic fields \(E\) = \(E\) \(j\) and \(B\) = \(B\) \(k\) :
1. Find the velocity (magnitude and direction) of a charged particle for which the Lorentz force is zero.
2. Using this result, describe how you would build a setup to select out only those particles in a beam moving at a certain velocity.
Determine qualitatively how a charged particle moves in crossed electric and magnetic fields in the general case in which it is not moving at constant velocity. For the sake of definiteness, assume that the magnetic field points in the +\(z \) direction and the electric field in the +\(x\) direction. Hint: Is there a reference frame in which the electric field vanishes? If there is, describe the motion in this reference frame and then determine how this motion looks in the original reference frame.
A horizontal wire of mass per unit length 0\(.\) 1 kg m^-1 passes through a horizontal magnetic field of strength \(B \) = 0\(.\) 1 T with an orientation of 45^∘ to the field as shown in figure 15.10. What current must the wire carry for the magnetic force on the wire to just balance gravity?
Figure 15.10: Horizontal wire with current \(i\) in a magnetic field.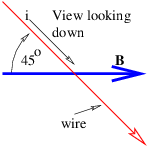
_____________________________________

Figure 15.11: Magnetic dipole (current loop) in an inhomogeneous magnetic field.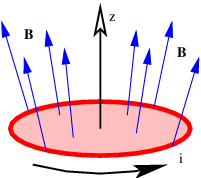
_____________________________________
Figure 15.11 shows a current loop in a magnetic field. The magnetic field diverges with increasing \(z\), so that its magnitude decreases with height.
1. Which way does the magnetic dipole vector due to the current loop point?
2. Is this dipole oriented so as to have maximum or minimum potential energy, or is it somewhere in between?
3. Is there a net force on the dipole? If so, what direction does it point? Hint: Determine the direction of the \(\mathbf{v} \times \mathbf{B}\) force at each point on the current loop. What direction does the sum of all these forces point?
Figure 15.12: A moving crossbar on a U-shaped wire in a magnetic field.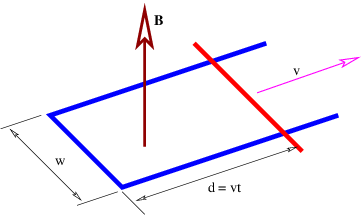
_____________________________________
A charged particle moving in a circle in a magnetic field constitutes a circular current which forms a magnetic dipole.
1. Determine whether the dipole moment produced by this current is aligned or anti-aligned with the initial magnetic field.
2. Do charged particles moving in a non-uniform magnetic field as shown in figure 15.11 tend to accelerate toward regions of stronger or weaker field?
Why do electric motors have many turns of wire around the loop that cuts the magnetic field, instead of just one? Hint: Magnetic fields in normal motors are of order 0\(.\) 1 T and currents are typically a few amps. Estimate the torque on a reasonably sized current loop for these conditions. Compare this to the torque you could expect to exert with your hand acting on a 1 m moment arm.
Imagine a stationary U-shaped conductor with a moving conducting bar in contact with the U as shown in figure 15.12. A uniform magnetic field exists normal to the plane of the U and has magnitude \(B\). The bar is moving outward along the U at speed \(v \) as shown.
1. Using the fact that the charged particles in the moving bar are subject to a Lorentz force due to the motion of the bar through a magnetic field, compute the EMF around the closed loop consisting of the bar and the U. Hint: Recall that the EMF is the work done per unit charge on a charged particle moving around the loop.
2. Compute the EMF around the above loop using Faraday’s law. Is the answer the same as obtained above?
Figure 15.13: The charged bead continuously accelerates around the loop due to electromagnetic fields.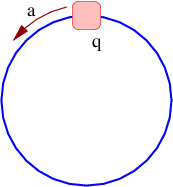
_____________________________________
A bead on a loop has a positive charge \(q\) and accelerates continuously around the loop in the counterclockwise direction, as shown in figure 15.13. Explain qualitatively what this information tells you about
1. the vector potential in the vicinity of the loop, and
2. the magnetic flux through the loop.