16.3: Gauss’s Law for Magnetism

By analogy with Gauss’s law for the electric field, we could write a Gauss’s law for the magnetic field as follows:

$$\Phi_{B}=C q_{\text{magnetic inside }}\label{16.11}$$

where $Φ_B$ is the outward magnetic flux through a closed surface, $C$ is a constant, and $q_{\text{magnetic inside}}$ is the “magnetic charge” inside the closed surface. Extensive searches have been made for magnetic charge, generally called a magnetic monopole. However, none has ever been found. Thus, Gauss’s law for magnetism can be written

$$\Phi_{B}=0 \quad \text { (Gauss's law for magnetism). }\label{16.12}$$

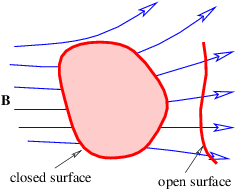
This of course doesn’t preclude non-zero values of the magnetic flux through open surfaces, as illustrated in Figure $\PageIndex{3}$:.

Figure $\PageIndex{3}$:: Illustration for Gauss’s law for magnetism. The net flux out of the closed surface is zero, but the flux through the open surface is not.