17.6: Problems

Last updated
Save as PDF

Page ID: 32854

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Compute the capacitance of an isolated conducting sphere of radius \(R\). Hint: Consider the other electrode to be a spherical shell surrounding the conducting sphere at very large radius.
Given a parallel plate capacitor with plate area \(S\), fixed charge ±\(q \) on the plates, and the possibly variable plate separation \(x\) :
1. Is the force between the plates attractive or repulsive?
2. Compute the magnitude of the force of each plate on the other. Hint: You know both the electric field and the charge.
3. Make an alternate computation of the force as follows: Compute the energy \(U \) in the electric field between the plates. The force is \(F \) = -\(dU∕dx\).
4. You probably found that the above two calculations of the force didn’t agree. Which is correct? Explain. Hint: In doing part (b), what part of the electric field acting on (say) the negative charge is due to itself, and what part is due to the positive charge? Only the latter part can exert a net force on the negative charge!
Compute the circulation of the vector field around the illustrated circle in the left panel of figure 17.3. Assume that the magnitude of the vector field equals \(Kr \) where \(K \) is a constant.
Compute the circulation of the vector field around the illustrated rectangle in the right panel of figure 17.3. Assume that the \(x \) component of the vector field equals \(Ky \) where \(K \) is a constant.
The solar wind consists of a plasma (a gas consisting of charged particles with equal amounts of positive and negative charge) streaming out from the sun. In certain sectors of the solar wind the magnetic field points away from the sun while in other sectors it points toward the sun. What is the magnitude and direction of the current flowing through the loop defined by the dashed rectangle that spans a sector boundary as shown in figure 17.9? Assume that the displacement current is negligible.
Figure 17.9: Magnetic field at a solar wind sector boundary.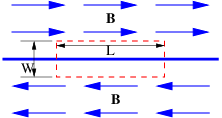
A superconducting parallel plate inductor with plate dimensions 0\(.\) 1 m by 0\(.\) 1 m and spacing 0\(.\) 01 m is held together by connectors with maximum breaking strength 500 N and has the input and the output connected by a superconducting wire. A current \(i \) is circulating through the inductor.
1. Is the force between the plates attractive or repulsive?
2. What is the maximum magnetic field that the inductor can have between the plates without blowing apart? Hint: Find the energy in the magnetic field as a function of plate separation and compute the force between the plates as for the capacitor. The magnetic flux through the inductor remains constant as the plates move in this case, which means that the current can change.
3. What is the current corresponding to the above maximum field?
Figure 17.10: Resistors in parallel and in series.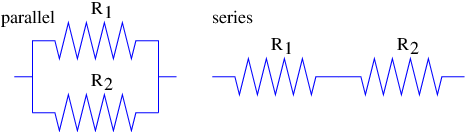
Use Kirchhoff’s laws to compute the net resistance of
1. resistors in parallel, and
2. resistors in series,
as shown in figure 17.10. Hint: In the first case the voltage drop across the resistors is the same, in the second, the current through the resistors is the same. Recall that Ohm’s law relates the current through a device to the voltage drop across it. (If you already know the answers, derive them; don’t just write them down.)

Figure 17.11: Battery in parallel with an inductor.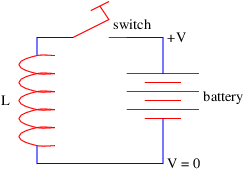
Try to explain in physical terms why doubling the length of a resistor doubles its resistance, while doubling its cross-sectional area halves its resistance. Use this argument to justify equation 17.18}.
Describe qualitatively what happens when
1. the switch is closed in the circuit in figure 17.11, and
2. when it is abruptly opened.
The battery produces a voltage difference \(V \), but also may be thought of as having a small internal resistance \(R\).

Figure 17.12: Circuit consisting of a shorted resistor.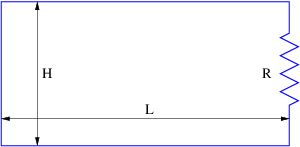
Given the circuit shown in figure 17.12:
1. What do Kirchhoff’s laws tell you about Δ\(ϕ \) across the resistor?
2. Suppose a time-varying magnetic field \(B \) = \(B\) ₀ sin(\(ωt\) ) is applied normal to the circuit loop, where \(B\) ₀ is a constant. What is the (time-dependent) voltage drop Δ\(ϕ \) across the resistor in this situation?
3. Given the above Δ\(ϕ\), what is the current through the resistor as a function of time?
You may ignore the effect of the current in creating an additional magnetic field.
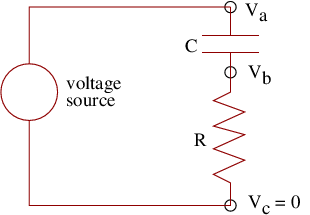
In the circuit shown in figure 17.13, the voltage source is switched on at time \(t \) = 0, at which the voltage \(V\) _A goes from zero to some constant positive value. The capacitor initially has no charge.
1. Just after the source is switched on what is the voltage \(V\) _B? Hint: Can the potential difference across the capacitor change instantaneously with the resistor in the circuit? Explain why or why not.
2. After a very long time, what is the voltage \(V\) _B?
3. Make a qualitative sketch of \(V\) _B as a function of time.
  Figure 17.13: Simple RC circuit.