18.3: The Geiger-Marsden Experiment

Figure 18.3: Schematic of Geiger-Marsden experiment. The radioactive source produces alpha particles that are collimated into a beam and directed at a gold foil. The alpha particles scatter off the foil and are detected by a flash of light when they hit the scintillation screen.

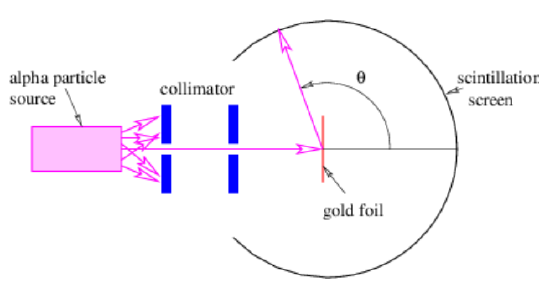
In 1908 Hans Geiger and Ernest Marsden, working with Ernest Rutherford of the Physical Laboratories at the University of Manchester, measured the angular distribution of alpha particles scattered from a thin gold foil in an experiment illustrated in figure 18.3. In order to understand this experiment, we need to compute the de Broglie wavelength of alpha particles resulting from radioactive decay. Typical alpha particle kinetic energies are of order \(5 \mathrm{MeV}=8 \times 10^{-13} \mathrm{~J}\). Since the alpha particle consists of two protons and two neutrons, its mass is about \(\mathrm{M}_{\mathrm{a}}=6.7 \times 10^{-27} \mathrm{~kg}\). This implies a velocity of about \(\mathrm{v}=1.1 \times 10^{7} \mathrm{~m} \mathrm{~s}^{-1}\), a momentum of about p = mv = 7.4 × 10^-20 N s, and a de Broglie wavelength of about \(\lambda=\mathrm{h} / \mathrm{p}=9.0 \times 10^{-15} \mathrm{~m}\).

Other evidence indicates that atoms have dimensions of order \(10^-10 m\), so the de Broglie wavelength of an alpha particle is about a factor of \(10^{4}\) smaller than a typical atomic dimension. Thus, the typical diffraction scattering angle of alpha particles off of atoms ought to be very small, of order \(a=\lambda /(2 d) \approx 10^{-4} \text { radian } \approx 0.01^{\circ}\).

Imagine the surprise of Geiger and Marsden when they found that while most alpha particles suffered only small deflections when passing through the gold foil, a small fraction of the incident particles scattered through large angles, some in excess of 90^∘!

Figure 18.4: Illustration of alpha particle trajectory in Rutherford’s model of the atom. The momentum transfer q from the nucleus to the alpha particle is equal to the change in the alpha particle’s momentum.

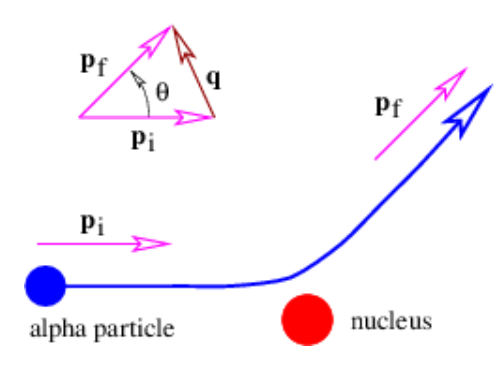
Ernest Rutherford calculated the probability for an alpha particle, considered to be a positive point charge, to be scattered through various angles by a stationary atomic nucleus, assumed also to be a positive point charge. The calculation was done classically, though interestingly enough a quantum mechanical calculation gives the same answer. The relative probability for scattering with a momentum transfer to the alpha particle of q is proportional to |q|^-4 ≡ q^-4 according to Rutherford’s calculation. (Do not confuse this q with charge!) As figure 18.4 indicates, a larger momentum transfer corresponds to a larger scattering angle. The maximum momentum transfer for an incident alpha particle with momentum p is 2|p|, or just twice the initial momentum. This corresponds to a head-on collision between the alpha particle and the nucleus followed by a recoil of the alpha particle directly backwards. Since this collision is elastic, the kinetic energy of the alpha particle after the collision is approximately the same as before, as long as the nucleus is much more massive than the alpha particle.

Rutherford’s calculation agreed quite closely with the experimental results of Geiger and Marsden. Though the probability for scattering through a large angle is small even in the Rutherford theory, it is still much larger than would be expected if there were no small scale atomic nucleus.