22.2: Heat

Two types of experiments suggest that heating is a form of energy transfer. First of all, on the macroscopic or everyday scale of things, there are forces that are apparently nonconservative. This is in marked contrast to the microscopic world, where forces are either conservative (gravity, electrostatics), don’t change a particle’s energy (magnetic force), or convert energy from one known form to another (non-static electric forces). With these fundamental forces all energy is accounted for — it is neither created or destroyed.

In contrast, macroscopic energy routinely disappears in the everyday world. Cars once set in motion don’t continue in motion forever on a level road once the engine is stopped; a soccer ball once kicked eventually comes to rest; electrical energy powering a light bulb appears to be lost. Careful measurements show that whenever this type of energy loss is found, heating occurs. Since we believe that macroscopic forces are really just large scale manifestations of fundamental microscopic forces, we do not believe that energy really disappears as a result of these forces — it must simply be converted from a form visible to us into an invisible form. We now know that such forces convert macroscopic energy to internal energy, a form of energy that is just the kinetic and potential energy of atomic and molecular motions. Thus, the apparent disappearance of macroscopic energy is just a consequence of the conversion of this energy into microscopic form.

Figure 22.2: Conversion of internal energy of gas in the cylinder to macroscopic energy. The work done by the force of the gas on the piston as it moves outward results in a decrease in temperature of the gas.

The second type of experiment that suggests that heating converts macroscopic energy to internal energy is one in which this energy is converted back to macroscopic form. An example of this process is illustrated in figure 22.2. As the piston moves out of the cylinder under the force exerted on it by the gas, work is done that can be stored or used by, say, compressing a spring or running an electric generator. As the piston moves out, the gas in the cylinder decreases in temperature, which indicates that the gas is losing microscopic energy.

Specific Heat

Conversion of macroscopic energy to microscopic kinetic energy thus tends to raise the temperature, while the reverse conversion lowers it. It is easy to show experimentally that the amount of heating needed to change the temperature of a body by some amount is proportional to the amount of matter in the body. Thus, it is natural to write

\[\Delta Q=M C \Delta T\label{22.4}\]

where \(M\) is the mass of material, \(\Delta \mathrm{Q}\) is the amount of energy transferred to the material, and \(\Delta \mathrm{T}\) is the change of the material’s temperature. The quantity \(C\) is called the specific heat of the material in question and is the amount of heating needed to raise the temperature of a unit mass of material by one degree. \(C\) varies with the type of material. Values for common materials are given in table 22.2.

Material	C (J kg^-1 K^-1)
brass	385
glass	669
ice	2092
steel	448
methyl alcohol	2510
glycerine	2427
water	4184

Table 22.2: Specific heats of common materials.

First Law of Thermodynamics

We now address some questions of terminology. The use of the terms “heat” and “quantity of heat” to indicate the amount of microscopic kinetic energy inhabiting a body has long been out of favor due to their association with the discredited “caloric” theory of heat. Instead, we use the term internal energy to describe the amount of microscopic energy in a body. The word heat is most correctly used only as a verb, e. g., “to heat the house”. Heat thus represents the transfer of internal energy from one body to another or conversion of some other form of energy to internal energy. Taking into account these definitions, we can express the idea of energy conservation in some material body by the equation

\[\Delta E=\Delta Q-\Delta W \quad \text { (first law of thermodynamics), }\label{22.5}\]

where \(\Delta \mathrm{E}\) is the change in internal energy resulting from the addition of heat \(\Delta \mathrm{Q}\) to the body and the work \(\Delta W\) done by the body on the outside world. This equation expresses the first law of thermodynamics. Note that the sign conventions are inconsistent as to the direction of energy flow. However, these conventions result from thinking about heat engines, i. e., machines that take in heat and put out macroscopic work. Examples of heat engines are steam engines, coal and nuclear power plants, the engine in your automobile, and the engines on jet aircraft.

Heat Conduction

Figure 22.3: Geometry of heat flow problem. Heat flows from higher to lower temperature.

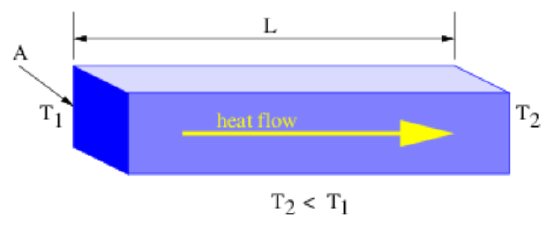
As noted earlier, internal energy may be transferred through a material from higher to lower temperature by a process known as heat conduction. The rate at which internal energy is transferred through a material body is known empirically to be proportional to the temperature difference across the body. For a rectangular body, the rate of transfer is also known to scale in proportion to the cross sectional area of the body perpendicular to the temperature gradient and to scale inversely with the distance over which the temperature difference exists. This is known as the law of heat conduction and is expressed in the following mathematical form:

\[F_{\text {heat }}=\frac{\kappa A \Delta T}{L}\label{22.6}\]

where \(F_{heat}\) is the internal energy per unit time flowing down the temperature gradient, A is the cross sectional area of the body normal to the internal energy flow direction, L is the length of the body in the direction of heat flow, \(\Delta \mathrm{T}\) is the temperature difference along its length, and κ is a constant characteristic of the material known as the thermal conductivity. The geometry is illustrated in figure 22.3 and the thermal conductivities of common materials are shown in table 22.3.

Material	κ (W m^-1 K^-1)
brass	109
brick	0.50
concrete	1.05
ice	2.2
paper	0.050
steel	46

Table 22.3: Values of thermal conductivity for common materials.

Thermal Radiation

Energy can also be transmitted though empty space by thermal radiation. This is nothing more than photons with a mixture of frequencies near a frequency \(\omega_{thermal}\) that is a function only of the temperature \(T\) of the body that is emitting them:

\[\omega_{\text {thermal }}=K T\label{22.7}\]

where the constant \(\mathrm{K}=3.67 \times 10^{11} \mathrm{~s}^{-1} \mathrm{~K}^{-1}\). The amount of thermal energy per unit area per unit time emitted by a material surface is called the flux of radiation and is given by Stefan’s law:

\[J_{E}=\varepsilon \sigma T^{4} \quad \text { (Stefan's law), }\label{22.8}\]

where \(\sigma=5.67 \times 10^{-8} \mathrm{~W} \mathrm{~m}^{-2} \mathrm{~K}^{-4}\) is the Stefan-Boltzmann constant and ε is the emissivity of the material surface. The emissivity lies in the range 0 ≤ ε ≤ 1 and depends on the type of material and the temperature of the surface.

Surfaces that emit thermal radiation at a particular frequency can also reflect radiation at that frequency. If \(J_{I}\) is the flux of radiation incident on the surface, then the reflected radiation is just

\[J_{R}=(1-\varepsilon) J_{I} \quad \text { (reflected radiation) }\label{22.9}\]

and the balance of the radiation is absorbed by the surface:

\[J_{A}=\varepsilon J_{I} \quad \text { (absorbed radiation). }\label{22.10}\]

Thus, high thermal emissivity goes along with high absorbed fraction and vice versa. A little thought indicates why this has to be so. If the emissivity were high and the absorption were low, then the object would spontaneously cool relative to its environment. If the reverse were true, it would spontaneously warm up. Thus, the universally observed behavior that internal energy flows from higher to lower temperatures would be violated.

Figure 22.4: Two surfaces facing each other, each with emissivity \(\varepsilon\) and temperature \(T\).

Imagine two surfaces of equal temperature \(T\) facing each other. The radiation emitted by one surface is partially absorbed and partially reflected from the other surface, as illustrated in figure 22.4. The total radiative flux, \(\mathrm{J}_{\text {tot }}\), coming from each surface is the sum of the reflected radiation originating from the other surface, \((1-\varepsilon)J_{\text {tot }}\), and the emitted thermal radiation, \(\varepsilon \sigma T^{4}\). Thus,

\[J_{t o t}=(1-\varepsilon) J_{t o t}+\varepsilon \sigma T^{4}\label{22.11}\]

Solving for \(\mathrm{J}_{\text {tot }}\), we find that

\[J_{t o t} \equiv J_{B B}=\sigma T^{4}\label{22.12}\]

Note that the total radiation originating from each surface, \(\mathrm{J}_{\text {tot }}\), is independent of the emissivity of the surfaces and depends only on the temperature. This radiative flux is called the black body flux. We give it the special name \(\mathrm{J}_{\mathrm{BB}}\). Because it no longer depends on \(\varepsilon\), it is independent of the character of the material making up the emitting surfaces. Different materials result in different fractions of thermal and reflected radiation, but the sum is always equal to the black body flux if both surfaces are at the same temperature. Planck’s arguments that led to the energy-frequency relationship of quantum mechanics, \(\mathrm{E}=\hbar \omega\), came from his attempt to explain black body radiation. The laws of black body radiation presented here can be derived from quantum mechanics.