6.4: Acceleration in Special Relativity

As noted above, acceleration is just the time rate of change of velocity. We use the above results to determine how acceleration transforms from one reference frame to another. Figure \(\PageIndex{4}\): shows the world line of an accelerated reference frame, with a time-varying velocity \(\mathrm{U}(\mathrm{t})\) relative to the unprimed inertial rest frame. Defining \(\Delta \mathrm{U}=\mathrm{U}(\mathrm{T})-\mathrm{U}(0)\) as the change in the velocity of the accelerated frame (relative to the unprimed frame) between events A and C, we can relate this to the change of velocity, \(\Delta \mathrm{U}^{\prime}\), of the accelerated frame relative to an inertial frame moving with the initial velocity, \(\mathrm{U}(0)\).

Figure \(\PageIndex{4}\):: World line of the origin of an accelerated reference frame.

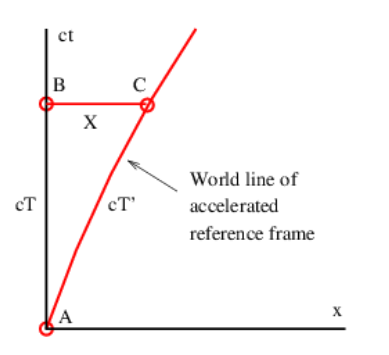
Applying the equation for the relativistic addition of velocities, we find

\[U(T)=U(0)+\Delta U=\frac{U(0)+\Delta U^{\prime}}{1+U(0) \Delta U^{\prime} / c^{2}}\label{6.10}\]

We now note that the mean acceleration of the reference frame between events A and C in the rest frame is just \(\mathrm{a}=\Delta \mathrm{U} / \mathrm{T}\), whereas the mean acceleration in the primed frame between the same two events is \(\mathrm{a}^{\prime}=\Delta \mathrm{U}^{\prime} / \mathrm{T}^{\prime}\). From equation (\ref{6.10}) we find that

\[\Delta U=\frac{\Delta U^{\prime}\left[1-U(0)^{2} / c^{2}\right]}{1+U(0) \Delta U^{\prime} / c^{2}}\label{6.11}\]

and the acceleration of the primed reference frame as it appears in the unprimed frame is

\[a=\frac{\Delta U}{T}=\frac{\Delta U^{\prime}\left[1-U(0)^{2} / c^{2}\right]}{T\left[1+U(0) \Delta U^{\prime} / c^{2}\right]}\label{6.12}\]

Since we are interested in the instantaneous rather than the average acceleration, we let \(T\) become small. This has three consequences. First, \(\Delta \mathrm{U} \text { and } \Delta \mathrm{U}^{\prime}\) become small, which means that the term \(\mathrm{U}(0) \Delta \mathrm{U}^{\prime} / \mathrm{c}^{2}\) in the denominator of Equation \ref{6.12} can be ignored compared to 1. This means that

\[a \approx \frac{\Delta U^{\prime}\left[1-U(0)^{2} / c^{2}\right]}{T}\label{6.13}\]

with the approximation becoming exact as T → 0. Second, the “triangle” with the curved side in Figure \(\PageIndex{4}\): becomes a true triangle, with the result that \(\mathrm{T}^{\prime}=\mathrm{T}\left[1-\mathrm{U}(0)^{2} / \mathrm{c}^{2}\right]^{1 / 2}\). The acceleration of the primed frame with respect to an inertial frame moving at speed \(\mathrm{U}(0)\) can therefore be written

\[a^{\prime}=\frac{\Delta U^{\prime}}{T^{\prime}}=\frac{\Delta U^{\prime}}{T\left[1-U(0)^{2} / c^{2}\right]^{1 / 2}}\label{6.14}\]

Third, we can replace U(0) with U, since the velocity of the accelerated frame doesn’t change very much over a short time interval.

Dividing equation (\ref{6.13}) by equation (\ref{6.14}) results in a relationship between the two accelerations:

\[a=a^{\prime}\left(1-U^{2} / c^{2}\right)^{3 / 2}\label{6.15}\]

which shows that the acceleration of a rapidly moving object, a, as observed from the rest frame, is less than its acceleration relative to an inertial reference frame in which the object is nearly stationary, \(\mathrm{a}^{\prime}\), by the factor \(\left(1-U^{2} / c^{2}\right)^{3 / 2}\). We call this latter acceleration the intrinsic acceleration. This difference in observed acceleration between the two inertial reference frames is purely the result of the geometry of space time, but it has interesting consequences.

Identifying a with \(\mathrm{dU} / \mathrm{dt}\), we can integrate the acceleration equation assuming that the intrinsic acceleration \(\mathrm{a}^{\prime}\) is constant and that the velocity \(U = 0\) at time \(t = 0\). We get the following result (verify this by differentiating with respect to time):

\[a^{\prime} t=\frac{U}{\left(1-U^{2} / c^{2}\right)^{1 / 2}}\label{6.16}\]

which may be solved for \(\mathrm{U} / \mathrm{c}\):

\[\frac{U}{c}=\frac{a^{\prime} t / c}{\left[1+\left(a^{\prime} t / c\right)^{2}\right]^{1 / 2}}\label{6.17}\]

This is plotted in Figure \(\PageIndex{5}\):. Classically, the velocity U would reach the speed of light when \(a^{\prime} t / c=1\). However, as figure 6.5 shows, the rate at which the velocity increases with time slows as the object moves faster, such that U approaches \(c\) asymptotically, but never reaches it.

Figure \(\PageIndex{5}\):: Velocity divided by the speed of light as a function of the product of the time and the (constant) acceleration divided by the speed of light.

The results for this section are valid only for acceleration components in the direction of motion. The components perpendicular to this direction behave differently and are treated in more advanced texts.