6.8: Problems

1. An object moves as described in figure 6.8, which shows its position x as a function of time t.
   1. Is the velocity positive, negative, or zero at each of the points A, B, C, D, E, and F?
   2. Is the acceleration positive, negative, or zero at each of the points A, B, C, D, E, and F? 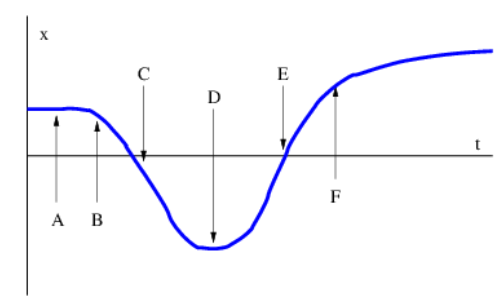Figure 6.8: Position of an object as a function of time.
2. An object is moving counterclockwise at constant speed around the circle shown in figure 6.9 due to the fact that it is attached by a string to the center of the circle at point O.
   1. Sketch the object’s velocity vectors at points A, B, and C.
   2. Sketch the object’s acceleration vectors at points A, B, and C.
   3. If the string breaks at point A, sketch the subsequent trajectory followed by the object. 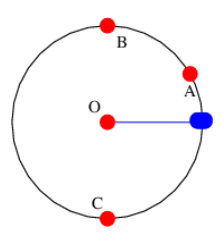Figure 6.9: Object in circular motion.
3. How fast are you going after accelerating from rest with intrinsic acceleration \(a=10 m s^{-2}\) after the given times measured in the rest frame:
   1. 10 y?
   2. 100000 y? Express your answer as the speed of light minus your actual speed. Hint: You may have a numerical problem on the second part, which you should try to resolve using the approximation \((1+\epsilon)^{\mathrm{X}} \approx 1+\mathrm{x} \epsilon\), which is valid for \(|\epsilon| \ll 1\).
4. An object’s world line is defined by \(x(t)=\left(d^{2}+c^{2} t^{2}\right)^{1 / 2}\) where d is a constant and c is the speed of light.
   1. Find the object’s velocity as a function of time.
   2. Using the above result, find the slope of the tangent to the world line as a function of time.
   3. Find where the line of simultaneity corresponding to each tangent world line crosses the x axis.
5. A car accelerates in the positive x direction at 3 m s^-2.
   1. What is the net force on a 100 kg man in the car as viewed from an inertial reference frame?
   2. What is the inertial force experienced by this man in the reference frame of the car?
   3. What is the net force experienced by the man in the car’s (accelerated) reference frame?
6. A person is sitting in a comfortable chair in her home in Bogotá, Colombia, which is essentially on the equator.
   1. What would the rotational period of the earth have to be to make this person weightless?
   2. What is her acceleration according to the equivalence principle in the earth frame in this situation?
7. At time t = 0 a Zork (a creature from the planet Zorkheim) accelerating to the right at a = 10³ m s^-2 in a spaceship accidently drops its stopwatch from the spaceship just when its velocity is zero.
   1. Describe qualitatively how the hands of the watch appear to move to the Zork as it observes the watch through a powerful telescope.
   2. After a very long time what does the watch read? Hint: Draw a spacetime diagram with the world lines of the spaceship and the watch. Then send light rays from the watch to the spaceship.
8. Using a spacetime diagram, show why signals from events on the hidden side of the event horizon from an accelerating spaceship cannot reach the spaceship.
9. Approximate equation (6.26) to first order in X′ for the case in which \(X^{\prime} \ll L\).
10. Imagine two identical clocks, one on top of the volcano Chimborazo in Ecuador (6300 m above sea level), the other in the Ecuadorian city of Guayaquil (at sea level).
    1. From the perspective of Chimborazo, does the clock in Guayaquil appear to be running faster or slower than the Chimborazo clock? Explain.
    2. Compute the fractional frequency difference \(\left(\omega-\omega^{\prime}\right) / \omega\) in this case, where ω is the freqency of the Guayaquil clock as observed in Guayaquil (and the frequency of the Chimborazo clock on Chimborazo) and \(\omega^{\prime}\) is the frequency of the Guayaquil clock as observed from Chimborazo. You may wish to use the results of the previous problem.