8.8: Problems

Last updated
Save as PDF

Page ID: 32976

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Suppose the dispersion relation for a matter wave under certain conditions is \(\omega=\mu+(\mathrm{k}-\mathrm{a})^{2} \mathrm{c}^{2} /(2 \mu)\) where k is the wavenumber of the wave, \(\mu=m c^{2} / \hbar\), m is the associated particle’s mass, a is a constant, c is the speed of light, and ℏ is Planck’s constant divided by 2\(\Pi\).
1. Use this disperson relation and the Planck and de Broglie relations to determine the relationship between energy E, momentum \(\Pi\), and mass m.
2. Compute the group velocity of the wave and use this to determine how the group velocity depends on mass and momentum in this case.
A matter wave function associated with a particle of definite (constant) total energy E takes the form shown in figure 8.5. Make a sketch showing how the kinetic, potential, and total energies of the particle vary with x. 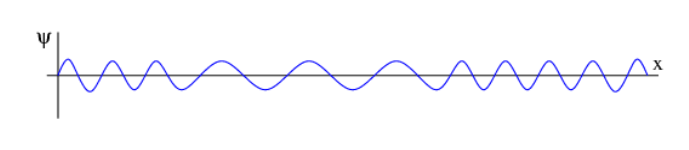Figure 8.5: A wave function in which the wavelength varies with position.
Compute \(\partial / \partial x \text { and } \partial / \partial y\) of the following functions. Other symbols are constants.
1. \(f(x, y)=a x^{2}+b y^{3}\)
2. \(f(x, y)=a x^{2} y^{2}\)
3. \(f(x, y)=(x+a)(y+b)\)
Given a potential energy for a particle of mass M of the form \(U(x)=A x^{3}-B x\) where A and B are positive constants:
1. Find the force on the particle.
2. Find the values of x where the force is zero.
3. Sketch U(x) versus x and graphically compare the slope of U(x) to the force computed above. Do the two qualitatively match?
4. If the total energy of the particle is zero, where are its turning points?
5. What is the particle’s speed as a function of position assuming that the total energy E is known?
Given a potential energy function \(U(x, y)=A\left(x^{2}+y^{2}\right)\) where A is a positive constant:
1. Sketch lines of constant U in the x-y plane.
2. Compute the components of force as a function of x and y and draw sample force vectors in the x-y plane on the same plot used above. Do the force vectors point “uphill” or “downhill”?
Do the same as in the previous question for the potential energy function \(U(x, y)=A x y\)
Suppose that the components of the force vector in the x-y plane are \(\mathbf{F}=\left(2 \mathrm{Axy}^{3}, 3 \mathrm{Ax}^{2} \mathrm{y}^{2}\right)\) where A is a constant. See if you can find a potential energy function U(x,y) which gives rise to this force.
You are standing on top of a cliff of height H with a rock of mass M.
1. If you throw the rock horizontally outward at speed u₀, what will its speed be when it hits the ground below?
2. If you throw the rock upward at 45^∘ to the horizontal at speed u₀, what will its speed be when it hits the ground? Hint: Can you use conservation of energy to solve this problem? Ignore air friction.
A car of mass 1200 kg initially moving \(30 \mathrm{~m} \mathrm{~s}^{-1}\) brakes to a stop.
1. What is the net work done on the car due to all the forces acting on it during the indicated period?
2. Describe the motion of the car relative to an inertial reference frame initially moving with the car.
3. In the above reference frame, what is the net work done on the car during the indicated period?Is work a relativistically invariant quantity? 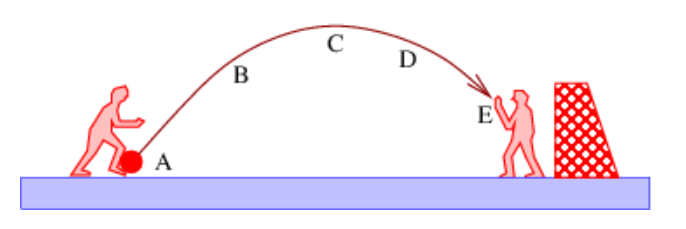Figure 8.6: The trajectory of a soccer ball.
A soccer player kicks a soccer ball, which is caught by the goal keeper as shown in figure 8.6. At various points forces exerted by gravity, air friction, the foot of the offensive player, and the hands of the goal keeper act on the ball.
1. List the forces acting on the soccer ball at each of the points A, B, C, D, and E.
2. State whether the instantaneous power being applied to the soccer ball due to each of the forces listed above is positive, negative, or zero at each of the labeled points.
A cannon located at \((x, z)=(0,0)\) shoots a cannon ball upward at an angle of θ from the horizontal at initial speed \(\mathrm{u}_{0}\). Hint: In order to solve this problem you must first obtain the x and z components of acceleration from Newton’s second law. Second, you must find the velocity components as a function of time from the components of acceleration. Third, you must find x and z as a function of time from the the components of velocity. Only then should you attempt to answer the questions below.
1. How long does it take the cannon ball to reach its peak altitude?
2. How high does the cannon ball go?
3. At what value of x does the cannon ball hit the ground (z = 0)?
4. Determine what value of θ yields the maximum range.