9.4: Problems

1. Suppose that a particle is represented by the wave function \(\Psi=\sin (\mathrm{kx}-\omega \mathrm{t})+\sin (-\mathrm{kx}-\omega \mathrm{t})\).
   1. Use trigonometry to simplify this wave function.
   2. Compute the x and t dependence of the probability of finding the particle by squaring the wave function.
   3. Explain what this result says about the time dependence of the probability of finding the particle. Does this make sense?
2. Repeat the above problem for a particle represented by the wave function \(\Psi=\exp [\mathrm{i}(\mathrm{kx}-\omega \mathrm{t})]+\exp [\mathrm{i}(-\mathrm{kx}-\omega \mathrm{t})]\).
3. Determine if the wavefunction \(\psi(x)=\exp \left(i C x^{2}\right)\) is invariant under displacement in the sense that the displaced wave function differs from the original wave function by just a phase factor.
4. Just as invariance under the substitution \(x \rightarrow x+D\) is associated with momentum, invariance under the substitution \(x \rightarrow-x\) is associated with a quantum mechanical variable called parity, denoted \(P\). However, unlike momentum, which can take on any numerical value, parity can take on only two possible values, \(\pm 1\). The parity of a wave function \(\Psi(x) \text { is }+1 \text { if } \Psi(-x)=\psi(x)\), while the parity is \(-1 \text { if } \Psi(-\mathrm{x})=-\Psi(\mathrm{x}) . \text { If } \Psi(\mathrm{x})\) satisfies neither of these conditions, then it has no definite value of parity.
   1. What is the parity of \(\Psi=\sin (\mathrm{kx}) ? \text { Of } \Psi=\cos (\mathrm{kx})\)? The quantity k is a constant.
   2. Is \(\psi(x)=\cos (k x)\) invariant under the substitution x = x + D for all possible values of D? Does this wave function have a definite value of the momentum?
   3. Show that a wave function with a definite value of the momentum does not have a definite value of parity. Are momentum and parity compatible variables?
5. Realizing that \(\cos (k x-\omega t)\) can be written in terms of complex exponential functions, give a physical interpretation of the meaning of the above cosine wave function. In particular, what are the possible values of the associated particle’s momentum and energy?
6. The time reversal operation T makes the substitution \(\mathrm{t} \rightarrow-\mathrm{t}\). Similar to parity, time reversal can only take on values \(\pm 1\). Is symmetry of a wave function under time reversal, i. e., \(\text { i. e., } \psi(-t)=\Psi(t)\), consistent with a definite value of the energy? Hint: Any wave function corresponding to a definite value of energy E must have the form \(\Psi=A \exp (-\mathrm{iEt} / \hbar)\) where A is not a function of time t. (Why?)
7. The operation C takes the complex conjugate of the wave function, i. e., it makes the substitution \(\mathrm{i} \rightarrow-\mathrm{i}\). In modern quantum mechanics this corresponds to interchanging particles and antiparticles, and is called charge conjugation. What does the combined operation CPT do to a complex plane wave, i. e., one with definite wave vector and frequency?
8. Make an energy level diagram for the case of a massless particle in a box.
9. Compare |Π| for the ground state of a non-relativistic particle in a box of size a with ΔΠ obtained from the uncertainty principle in this situation. Hint: What should you take for \(\Delta \mathrm{x}\)?
10. Imagine that a billiard table has an infinitely high rim around it. For this problem assume that \(\hbar=1 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}\).
    1. If the table is 1.5 m long and if the mass of a billiard ball is M = 0.5 kg, what is the billiard ball’s lowest or ground state energy? Hint: Even though the billiard table is two dimensional, treat this as a one-dimensional problem. Also, treat the problem nonrelativistically and ignore the contribution of the rest energy to the total energy.
    2. The energy required to lift the ball over a rim of height H against gravity is \(\mathrm{U}=\mathrm{MgH} \text { where } \mathrm{g}=9.8 \mathrm{~m} \mathrm{~s}^{-2}\). What rim height makes the gravitational potential energy equal to the ground state energy of the billiard ball calculated above.
    3. If the rim is actually twice as high as calculated above but is only 0.1 m thick, determine the probability of the ball penetrating the rim. 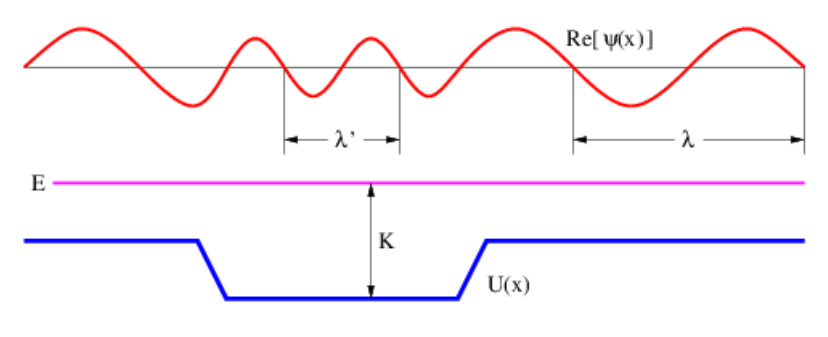Figure \(\PageIndex{7}\):: Real part of the wave function ψ, corresponding to a fixed total energy E, occurring in a region of spatially variable potential energy \(\mathrm{U}(\mathrm{x})\). Notice how the wavelength \(\lambda\) changes as the kinetic energy \(\mathrm{K}=\mathrm{E}-\mathrm{U}\) changes.
11. The real part of the wave function of a particle with positive energy E passing through a region of negative potential energy is shown in Figure \(\PageIndex{7}\):.
    1. If the total energy is definitely E, what is the dependence of this wave function on time?
    2. Is the wave function invariant under displacement in space in this case? Why or why not?
    3. Does this wave function correspond to a definite value of momentum? Why or why not?
    4. Is the momentum compatible with the energy in this case? Why or why not?
12. Assuming again that \(\hbar=1 \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-1}\), what are the possible speeds of a toy train of mass 3 kg running around a circular track of radius 0.8 m?
13. If a particle of zero mass sliding around a circular loop of radius R can take on angular momenta \(\mathrm{L}_{\mathrm{m}}=\mathrm{m} \hbar\) where \(m\) is an integer, what are the possible kinetic energies of the particle? Hint: Remember that \(\mathrm{L}=\Pi \mathrm{R}\).