11.8: Evolution of the Early Universe
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the evolution of the early universe in terms of the four fundamental forces
- Use the concept of gravitational lensing to explain astronomical phenomena
- Provide evidence of the Big Bang in terms of cosmic background radiation
- Distinguish between dark matter and dark energy
In the previous section, we discussed the structure and dynamics of universe. In particular, the universe appears to be expanding and even accelerating. But what was the universe like at the beginning of time? In this section, we discuss what evidence scientists have been able to gather about the early universe and its evolution to present time.
The Early Universe
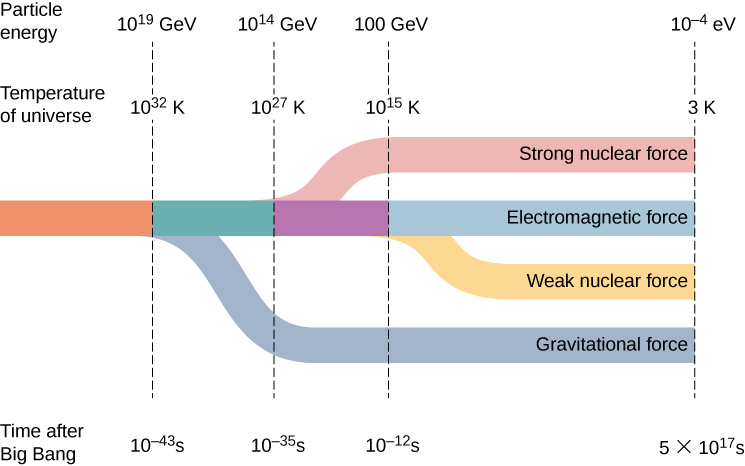
Before the short period of cosmic inflation, cosmologists believe that all matter in the universe was squeezed into a space much smaller than an atom. Cosmologists further believe that the universe was extremely dense and hot, and interactions between particles were governed by a single force. In other words, the four fundamental forces (strong nuclear, electromagnetic, weak nuclear, and gravitational) merge into one at these energies (Figure 11.8.1). How and why this “unity” breaks down at lower energies is an important unsolved problem in physics.
Scientific models of the early universe are highly speculative. Figure 11.8.2 shows a sketch of one possible timeline of events.
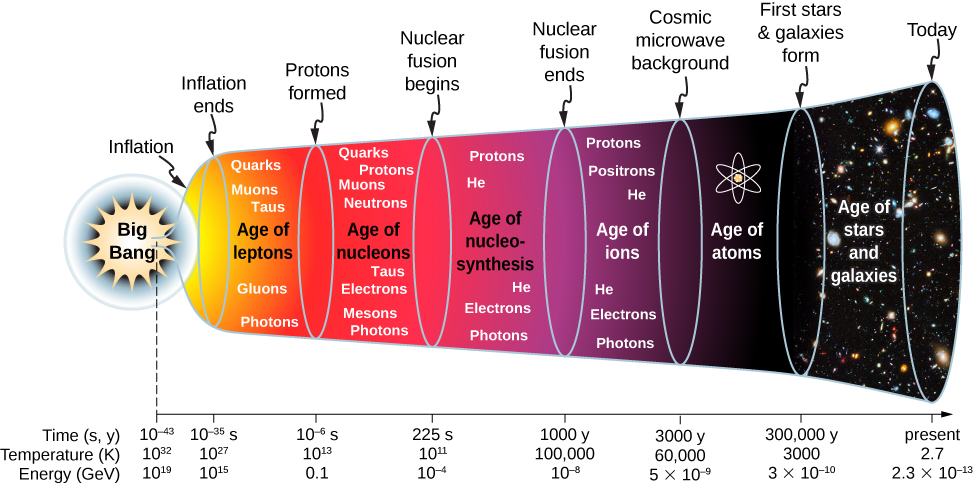
- Big Bang (t<10−43s): The current laws of physics break down. At the end of the initial Big Bang event, the temperature of the universe is approximately T=1032K.
- Inflationary phase (t=10−43to10−35): The universe expands exponentially, and gravity separates from the other forces. The universe cools to approximately T=1027K.
- Age of leptons (t=10−35to10−6s): As the universe continues to expand, the strong nuclear force separates from the electromagnetic and weak nuclear forces (or electroweak force). Soon after, the weak nuclear force separates from the electromagnetic force. The universe is a hot soup of quarks, leptons, photons, and other particles.
- Age of nucleons (t=10−6to225s): The universe consists of leptons and hadrons (such as protons, neutrons, and mesons) in thermal equilibrium. Pair production and pair annihilation occurs with equal ease, so photons remain in thermal equilibrium: γ+γ⇌e−+e+ γ+γ⇌p+¯p γ+γ⇌n+¯n. The number of protons is approximately equal to the number of neutrons through interactions with neutrinos: νe+n⇌e−+p ¯νe+p⇌e++n. The temperature of the universe settles to approximately 1011K —much too cool for the continued production of nucleon-antinucleon pairs. The numbers of protons and neutrons begin to dominate over their anti-particles, so proton-antiproton (p¯p) and neutron-antineutron (n¯n) annihilations decline. Deuterons (proton-neutron pairs) begin to form.
- Age of nucleosynthesis (t=225s to 1000 years): As the universe continues to expand, deuterons react with protons and neutrons to form larger nuclei; these larger nuclei react with protons and neutrons to form still larger nuclei. At the end of this period, about 1/4 of the mass of the universe is helium. (This explains the current amount of helium in the universe.) Photons lack the energy to continue electron-positron production, so electrons and positrons annihilate each other to photons only.
- Age of ions (t=1000 to 3000 years): The universe is hot enough to ionize any atoms formed. The universe consists of electrons, positrons, protons, light nuclei, and photons.
- Age of atoms (3000 to 300,000 years): The universe cools below 105K and atoms form. Photons do not interact strongly with neutral atoms, so they “decouple” (separate) from atoms. These photons constitute the cosmic microwave background radiation to be discussed later.
- Age of stars and galaxies (t=300,000 years to present): The atoms and particles are pulled together by gravity and form large lumps. The atoms and particles in stars undergo nuclear fusion reaction.
Watch this video to learn more about Big Bang cosmology.
To describe the conditions of the early universe quantitatively, recall the relationship between the average thermal energy of particle (E) in a system of interacting particles and equilibrium temperature (T) of that system: E=kBT, where kB is Boltzmann’s constant. In the hot conditions of the early universe, particle energies were unimaginably large.
Strategy
The average thermal energy of a particle in a system of interacting particles depends on the equilibrium temperature of that system. We are given this approximate temperature in the above timeline.
Solution
Cosmologists think the temperature of the universe just after the Big Bang was approximately T=1032K. Therefore, the average thermal energy of a particle would have been
kBT≈(10−4eV/K)(1032K)=1028eV=1019GeV.
Significance
This energy is many orders of magnitude larger than particle energies produced by human-made particle accelerators. Currently, these accelerators operate at energies less than 104GeV.
Compare the abundance of helium by mass 10,000 years after the Big Bang and now.
- Answer
-
about the same
Nucleons form at energies approximately equal to the rest mass of a proton, or 1000 MeV. The temperature corresponding to this energy is therefore
T=1000MeV8.62×1011MeV⋅K−1=1.2×1013K.
Temperatures of this value or higher existed within the first second of the early universe. A similar analysis can be done for atoms. Atoms form at an energy equal to the ionization energy of ground-state hydrogen (13 eV). The effective temperature for atom formation is therefore
T=13eV8.62×105eV⋅K−1=1.6×105K.
This occurs well after the four fundamental forces have separated, including forces necessary to bind the protons and neutrons in the nucleus (strong nuclear force), and bind electrons to the nucleus (electromagnetic force).
Nucleosynthesis of Light Elements
The relative abundances of the light elements hydrogen, helium, lithium, and beryllium in the universe provide key evidence for the Big Bang. The data suggest that much of the helium in the universe is primordial. For instance, it turns out that that 25% of the matter in the universe is helium, which is too high an abundance and cannot be explained based on the production of helium in stars.
How much of the elements in the universe were created in the Big Bang? If you run the clock backward, the universe becomes more and more compressed, and hotter and hotter. Eventually, temperatures are reached that permit nucleosynthesis, the period of formation of nuclei, similar to what occurs at the core of the Sun. Big Bang nucleosynthesis is believed to have occurred within a few hundred seconds of the Big Bang.
How did Big Bang nucleosynthesis occur? At first, protons and neutrons combined to form deuterons, 2H. The deuteron captured a neutron to form triton, 3H - the nucleus of the radioactive hydrogen called tritium. Deuterons also captured protons to make helium 3He. When 3H captures a proton or 3He captures a neutron, helium 4He results. At this stage in the Big Bang, the ratio of protons to neutrons was about 7:1. Thus, the process of conversion to 4He used up almost all neutrons. The process lasted about 3 minutes and almost 25% of all the matter turned into 4He, along with small percentages of 2H, 3H and 3He. Tiny amounts of 7Li and 7Be were also formed. The expansion during this time cooled the universe enough that the nuclear reactions stopped. The abundances of the light nuclei 2H, 4He, and 7Li created after the Big Bang are very dependent on the matter density.
The predicted abundances of the elements in the universe provide a stringent test of the Big Bang and the Big Bang nucleosynthesis. Recent experimental estimates of the matter density from the Wilkinson Microwave Anisotropy Probe (WMAP) agree with model predictions. This agreement provides convincing evidence of the Big Bang model.
Cosmic Microwave Background Radiation
According to cosmological models, the Big Bang event should have left behind thermal radiation called the cosmic microwave background radiation (CMBR). The intensity of this radiation should follow the blackbody radiation curve (Photons and Matter Waves). Wien’s law states that the wavelength of the radiation at peak intensity is
λmax=2.898×10−3m⋅KT,
where T is temperature in kelvins. Scientists expected the expansion of the universe to “stretch the light,” and the temperature to be very low, so cosmic background radiation should be long-wavelength and low energy.
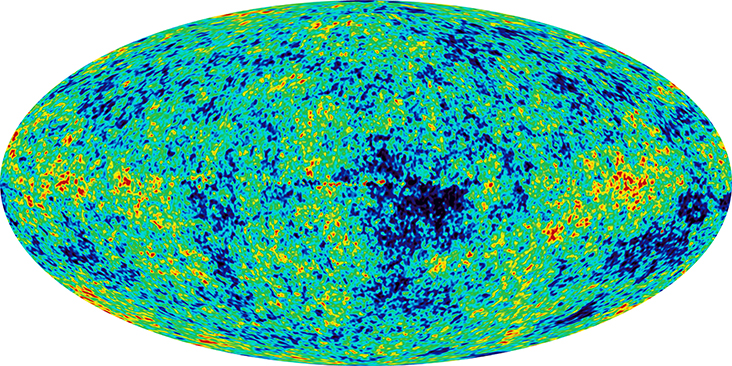
In the 1960s, Arno Penzias and Robert Wilson of Bell Laboratories noticed that no matter what they did, they could not get rid of a faint background noise in their satellite communication system. The noise was due to radiation with wavelengths in the centimeter range (the microwave region). Later, this noise was associated with the cosmic background radiation. An intensity map of the cosmic background radiation appears in Figure 11.8.3. The thermal spectrum is modeled well by a blackbody curve that corresponds to a temperature T=2.7K (Figure 11.8.4).

The formation of atoms in the early universe makes these atoms less likely to interact with light. Therefore, photons that belong to the cosmic background radiation must have separated from matter at a temperature T associated with 1 eV (the approximate ionization energy of an atom) . The temperature of the universe at this point was
kBT∼1eV⇒T=1eV8.617×105eV/K∼104K.
According to cosmological models, the time when photons last scattered off charged particles was approximately 380,000 years after the Big Bang. Before that time, matter in the universe was in the plasma form and the photons were “thermalized.”
Antimatter and Matter
We know from direct observation that antimatter is rare. Earth and the solar system are nearly pure matter, and most of the universe also seems dominated by matter. This is proven by the lack of annihilation radiation coming to us from space, particularly the relative absence of 0.511-MeV γ rays created by the mutual annihilation of electrons and positrons. (Antimatter in nature is created in particle collisions and in β+ decays, but only in small amounts that quickly annihilate, leaving almost pure matter surviving.)
Despite the observed dominance of matter over antimatter in the universe, the Standard Model of particle interactions and experimental measurement suggests only small differences in the ways that matter and antimatter interact. For example, neutral kaon decays produce only slightly more matter than antimatter. Yet, if through such decay, slightly more matter than antimatter was produced in the early universe, the rest could annihilate pair by pair, leaving mostly ordinary matter to form the stars and galaxies. In this way, the vast number of stars we observe may be only a tiny remnant of the original matter created in the Big Bang.
Dark Matter and Dark Energy
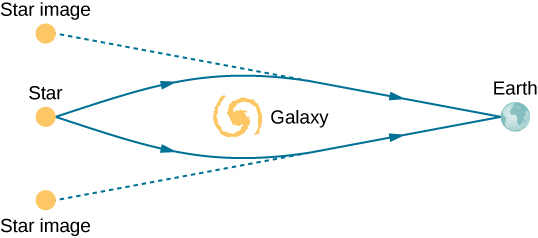
In the last two decades, new and more powerful techniques have revealed that the universe is filled with dark matter. This type of matter is interesting and important because, currently, scientists do not know what it is! However, we can infer its existence by the deflection of distant starlight. For example, if light from a distant galaxy is bent by the gravitational field of a clump of dark matter between us and the galaxy, it is possible that two images of the same galaxy can be produced (Figure 11.8.5). The bending of light by the gravitational field of matter is called gravitational lensing. In some cases, the starlight travels to an observer by multiple paths around the galaxy, producing a ring (Figure 11.8.6).
Based on current research, scientist know only that dark matter is cold, slow moving, and interacts weakly with ordinary matter. Dark matter candidates include neutralinos (partners of Z bosons, photons, and Higgs bosons in “supersymmetry theory”) and particles that circulate in tiny rings set up by extra spatial dimensions.

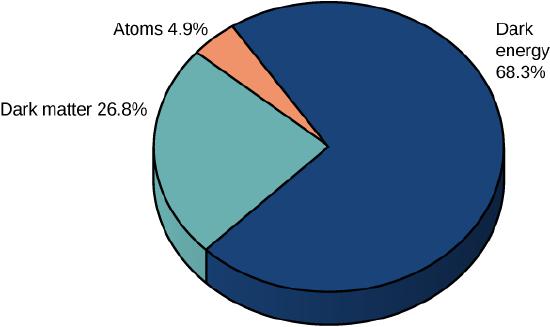
Increasingly precise astronomical measurements of the expanding universe also reveal the presence of a new form of energy called dark energy. This energy is thought to explain larger-than-expected values for the observed galactic redshifts for distant galaxies. These redshifts suggest that the universe is not only expanding, but expanding at an increasing rate. Virtually nothing is known about the nature and properties of dark energy. Together, dark energy and dark matter represent two of the most interesting and unsolved puzzles of modern physics. Scientists attribute 68.3% of the energy of the universe to dark energy, 26.8% to dark matter, and just 4.9% to the mass-energy of ordinary particles (Figure 11.8.7).
Given the current great mystery over the nature of dark matter and dark energy, Isaac Newton’s humble words are as true now as they were centuries ago: “I do not know what I may appear to the world, but to myself I seem to have been only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me.”


