1.6: Phase Changes
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe phase transitions and equilibrium between phases
- Solve problems involving latent heat
- Solve calorimetry problems involving phase changes
Phase transitions play an important theoretical and practical role in the study of heat flow. In melting (or “fusion”), a solid turns into a liquid; the opposite process is freezing. In evaporation, a liquid turns into a gas; the opposite process is condensation.
A substance melts or freezes at a temperature called its melting point, and boils (evaporates rapidly) or condenses at its boiling point. These temperatures depend on pressure. High pressure favors the denser form, so typically, high pressure raises the melting point and boiling point, and low pressure lowers them. For example, the boiling point of water is 100oC at 1.00 atm. At higher pressure, the boiling point is higher, and at lower pressure, it is lower. The main exception is the melting and freezing of water, discussed in the next section.
Phase Diagrams
The phase of a given substance depends on the pressure and temperature. Thus, plots of pressure versus temperature showing the phase in each region provide considerable insight into thermal properties of substances. Such a pT graph is called a phase diagram.
Figure 1.6.1 shows the phase diagram for water. Using the graph, if you know the pressure and temperature, you can determine the phase of water. The solid curves—boundaries between phases—indicate phase transitions, that is, temperatures and pressures at which the phases coexist. For example, the boiling point of water is 100oC at 1.00 atm. As the pressure increases, the boiling temperature rises gradually to 374oC at a pressure of 218 atm. A pressure cooker (or even a covered pot) cooks food faster than an open pot, because the water can exist as a liquid at temperatures greater than 100oC without all boiling away. (As we’ll see in the next section, liquid water conducts heat better than steam or hot air.) The boiling point curve ends at a certain point called the critical point—that is, a critical temperature, above which the liquid and gas phases cannot be distinguished; the substance is called a supercritical fluid. At sufficiently high pressure above the critical point, the gas has the density of a liquid but does not condense. Carbon dioxide, for example, is supercritical at all temperatures above 31oC. Critical pressure is the pressure of the critical point.
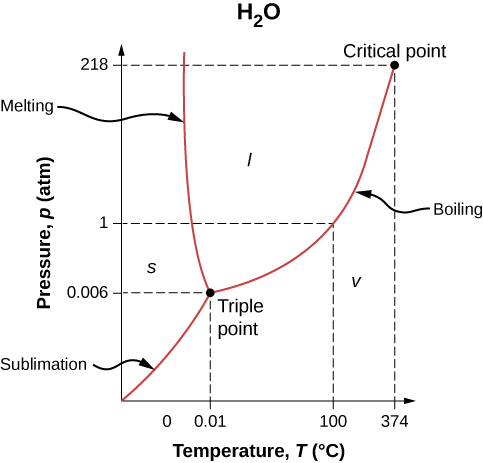
Similarly, the curve between the solid and liquid regions in Figure 1.6.1 gives the melting temperature at various pressures. For example, the melting point is 0oC at 1.00 atm, as expected. Water has the unusual property that ice is less dense than liquid water at the melting point, so at a fixed temperature, you can change the phase from solid (ice) to liquid (water) by increasing the pressure. That is, the melting temperature of ice falls with increased pressure, as the phase diagram shows. For example, when a car is driven over snow, the increased pressure from the tires melts the snowflakes; afterwards, the water refreezes and forms an ice layer.
As you learned in the earlier section on thermometers and temperature scales, the triple point is the combination of temperature and pressure at which ice, liquid water, and water vapor can coexist stably—that is, all three phases exist in equilibrium. For water, the triple point occurs at 273.16K(0.01oC) and 611.2 Pa; that is a more accurate calibration temperature than the melting point of water at 1.00 atm, or 273.15K(0.0oC).
View this video to see a substance at its triple point.
At pressures below that of the triple point, there is no liquid phase; the substance can exist as either gas or solid. For water, there is no liquid phase at pressures below 0.00600 atm. The phase change from solid to gas is called sublimation. You may have noticed that snow can disappear into thin air without a trace of liquid water, or that ice cubes can disappear in a freezer. Both are examples of sublimation. The reverse also happens: Frost can form on very cold windows without going through the liquid stage. Figure 1.6.2 shows the result, as well as showing a familiar example of sublimation. Carbon dioxide has no liquid phase at atmospheric pressure. Solid CO2 is known as dry ice because instead of melting, it sublimes. Its sublimation temperature at atmospheric pressure is −78oC. Certain air fresheners use the sublimation of a solid to spread a perfume around a room. Some solids, such as osmium tetroxide, are so toxic that they must be kept in sealed containers to prevent human exposure to their sublimation-produced vapors.

Equilibrium
At the melting temperature, the solid and liquid phases are in equilibrium. If heat is added, some of the solid will melt, and if heat is removed, some of the liquid will freeze. The situation is somewhat more complex for liquid-gas equilibrium. Generally, liquid and gas are in equilibrium at any temperature. We call the gas phase a vapor when it exists at a temperature below the boiling temperature, as it does for water at 20.0oC. Liquid in a closed container at a fixed temperature evaporates until the pressure of the gas reaches a certain value, called the vapor pressure, which depends on the gas and the temperature. At this equilibrium, if heat is added, some of the liquid will evaporate, and if heat is removed, some of the gas will condense; molecules either join the liquid or form suspended droplets. If there is not enough liquid for the gas to reach the vapor pressure in the container, all the liquid eventually evaporates.
If the vapor pressure of the liquid is greater than the total ambient pressure, including that of any air (or other gas), the liquid evaporates rapidly; in other words, it boils. Thus, the boiling point of a liquid at a given pressure is the temperature at which its vapor pressure equals the ambient pressure. Liquid and gas phases are in equilibrium at the boiling temperature (Figure 1.6.3). If a substance is in a closed container at the boiling point, then the liquid is boiling and the gas is condensing at the same rate without net change in their amounts.
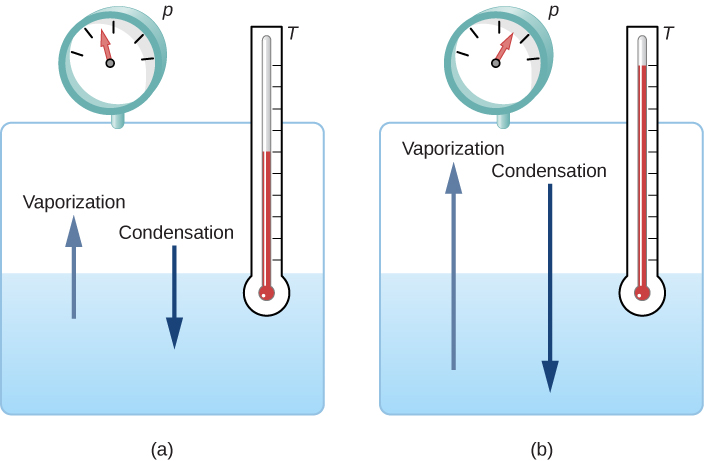
For water, 100oC is the boiling point at 1.00 atm, so water and steam should exist in equilibrium under these conditions. Why does an open pot of water at 100oC boil completely away? The gas surrounding an open pot is not pure water: it is mixed with air. If pure water and steam are in a closed container at 100oC and 1.00 atm, they will coexist—but with air over the pot, there are fewer water molecules to condense, and water boils away. Another way to see this is that at the boiling point, the vapor pressure equals the ambient pressure. However, part of the ambient pressure is due to air, so the pressure of the steam is less than the vapor pressure at that temperature, and evaporation continues. Incidentally, the equilibrium vapor pressure of solids is not zero, a fact that accounts for sublimation.
Explain why a cup of water (or soda) with ice cubes stays at 0oC even on a hot summer day.
- Answer
-
The ice and liquid water are in thermal equilibrium, so that the temperature stays at the freezing temperature as long as ice remains in the liquid. (Once all of the ice melts, the water temperature will start to rise.)
Phase Change and Latent Heat
So far, we have discussed heat transfers that cause temperature change. However, in a phase transition, heat transfer does not cause any temperature change.
For an example of phase changes, consider the addition of heat to a sample of ice at −20oC (Figure 1.6.4) and atmospheric pressure. The temperature of the ice rises linearly, absorbing heat at a constant rate of 2090J/kg⋅oC until it reaches 0oC. Once at this temperature, the ice begins to melt and continues until it has all melted, absorbing 333 kJ/kg of heat. The temperature remains constant at 0oC during this phase change. Once all the ice has melted, the temperature of the liquid water rises, absorbing heat at a new constant rate of 4186J/kg⋅oC. At 100oC the water begins to boil. The temperature again remains constant during this phase change while the water absorbs 2256 kJ/kg of heat and turns into steam. When all the liquid has become steam, the temperature rises again, absorbing heat at a rate of 2020J/kg⋅oC. If we started with steam and cooled it to make it condense into liquid water and freeze into ice, the process would exactly reverse, with the temperature again constant during each phase transition.
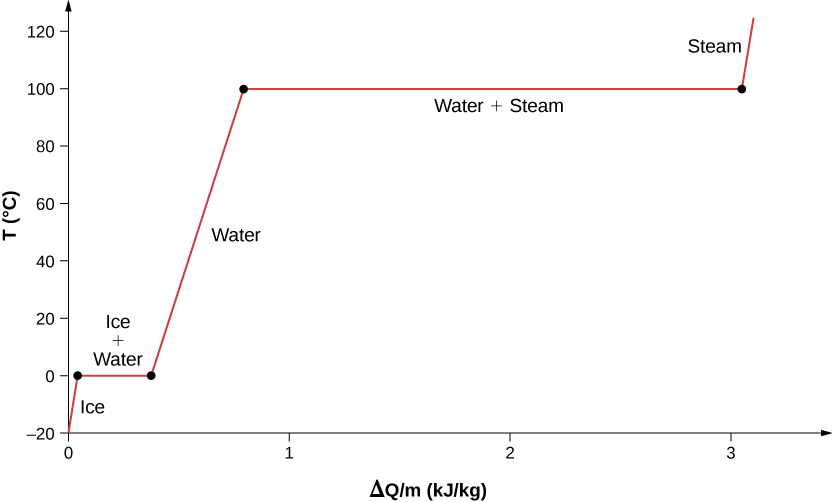
Where does the heat added during melting or boiling go, considering that the temperature does not change until the transition is complete? Energy is required to melt a solid, because the attractive forces between the molecules in the solid must be broken apart, so that in the liquid, the molecules can move around at comparable kinetic energies; thus, there is no rise in temperature. Energy is needed to vaporize a liquid for similar reasons. Conversely, work is done by attractive forces when molecules are brought together during freezing and condensation. That energy must be transferred out of the system, usually in the form of heat, to allow the molecules to stay together (Figure 1.6.4). Thus, condensation occurs in association with cold objects—the glass in Figure 1.6.5, for example.

The energy released when a liquid freezes is used by orange growers when the temperature approaches 0oC. Growers spray water on the trees so that the water freezes and heat is released to the growing oranges. This prevents the temperature inside the orange from dropping below freezing, which would damage the fruit (Figure 1.6.6).

The energy involved in a phase change depends on the number of bonds or force pairs and their strength. The number of bonds is proportional to the number of molecules and thus to the mass of the sample. The energy per unit mass required to change a substance from the solid phase to the liquid phase, or released when the substance changes from liquid to solid, is known as the heat of fusion. The energy per unit mass required to change a substance from the liquid phase to the vapor phase is known as the heat of vaporization. The strength of the forces depends on the type of molecules. The heat Q absorbed or released in a phase change in a sample of mass m is given by
Q=mLf(melting/freezing)
Q=mLv(vaporization/condensation)
where the latent heat of fusion Lf and latent heat of vaporization Lv are material constants that are determined experimentally. (Latent heats are also called latent heat coefficients and heats of transformation.) These constants are “latent,” or hidden, because in phase changes, energy enters or leaves a system without causing a temperature change in the system, so in effect, the energy is hidden.
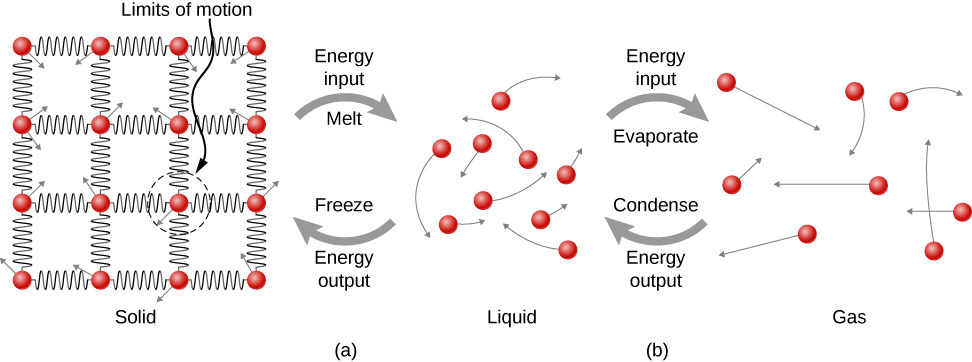
Table 1.6.1 lists representative values of Lf and Lv in kJ/kg, together with melting and boiling points. Note that in general, Lv>Lf. The table shows that the amounts of energy involved in phase changes can easily be comparable to or greater than those involved in temperature changes, as Figure 1.6.7 and the accompanying discussion also showed.
| Lf | Lv | |||||
|---|---|---|---|---|---|---|
| Substance | Melting Point (oC) | kJ/kg | kcal/kg | Boiling Point (oC) | kJ/kg | kcal/kg |
| Helium[2] | −272.2(0.95K) | 5.23 | 1.25 | −268.9(4.2K) | 20.9 | 4.99 |
| Hydrogen | −259.3(13.9K) | 58.6 | 14.0 | −252.9(20.2K) | 452 | 108 |
| Nitrogen | −210.0(63.2K) | 25.5 | 6.09 | −195.8(77.4K) | 201 | 48.0 |
| Oxygen | −218.8(54.4K) | 13.8 | 3.30 | −183.0(90.2K) | 213 | 50.9 |
| Ethanol | –114 | 104 | 24.9 | 78.3 | 854 | 204 |
| Ammonia | –75 | 332 | 79.3 | –33.4 | 1370 | 327 |
| Mercury | –38.9 | 11.8 | 2.82 | 357 | 272 | 65.0 |
| Water | 0.00 | 334 | 79.8 | 100.0 | 2256[3] | 539[4] |
| Sulfur | 119 | 38.1 | 9.10 | 444.6 | 326 | 77.9 |
| Lead | 327 | 24.5 | 5.85 | 1750 | 871 | 208 |
| Antimony | 631 | 165 | 39.4 | 1440 | 561 | 134 |
| Aluminum | 660 | 380 | 90 | 2450 | 11400 | 2720 |
| Silver | 961 | 88.3 | 21.1 | 2193 | 2336 | 558 |
| Gold | 1063 | 64.5 | 15.4 | 2660 | 1578 | 377 |
| Copper | 1083 | 134 | 32.0 | 2595 | 5069 | 1211 |
| Uranium | 1133 | 84 | 20 | 3900 | 1900 | 454 |
| Tungsten | 3410 | 184 | 44 | 5900 | 4810 | 1150 |
| Values quoted at the normal melting and boiling temperatures at standard atmospheric pressure (1atm). [2]Helium has no solid phase at atmospheric pressure. The melting point given is at a pressure of 2.5 MPa. [3]At 37.0oC (body temperature), the heat of vaporization Lv for water is 2430 kJ/kg or 580 kcal/kg. [4]At 37.0oC (body temperature), the heat of vaporization, Lv for water is 2430 kJ/kg or 580 kcal/kg. | ||||||
Phase changes can have a strong stabilizing effect on temperatures that are not near the melting and boiling points, since evaporation and condensation occur even at temperatures below the boiling point. For example, air temperatures in humid climates rarely go above approximately 38.0oC because most heat transfer goes into evaporating water into the air. Similarly, temperatures in humid weather rarely fall below the dew point—the temperature where condensation occurs given the concentration of water vapor in the air—because so much heat is released when water vapor condenses.
More energy is required to evaporate water below the boiling point than at the boiling point, because the kinetic energy of water molecules at temperatures below 100oC is less than that at 100oC, so less energy is available from random thermal motions. For example, at body temperature, evaporation of sweat from the skin requires a heat input of 2428 kJ/kg, which is about 10% higher than the latent heat of vaporization at 100oC. This heat comes from the skin, and this evaporative cooling effect of sweating helps reduce the body temperature in hot weather. However, high humidity inhibits evaporation, so that body temperature might rise, while unevaporated sweat might be left on your brow.
Three ice cubes are used to chill a soda at 20oC with mass msoda=0.25kg. The ice is at 0oC and each ice cube has a mass of 6.0 g. Assume that the soda is kept in a foam container so that heat loss can be ignored and that the soda has the same specific heat as water. Find the final temperature when all ice has melted.
Strategy
The ice cubes are at the melting temperature of 0oC. Heat is transferred from the soda to the ice for melting. Melting yields water at 0oC, so more heat is transferred from the soda to this water until the water plus soda system reaches thermal equilibrium.
The heat transferred to the ice is
Qice=miceLf+micecw(Tf−0oC).
The heat given off by the soda is
Qsoda=msodacw(Tf−20oC).
Since no heat is lost, Qice=−Qsoda, as in Example 1.5.3, so that
miceLf+micecw(Tf−0oC)=−msodacw(Tf−20oC).
Solve for the unknown quantity
Tf=msodacw(20oC)−miceLf(msoda+mice)cw
Solution
First we identify the known quantities. The mass of ice is mice=3×6.0g=0.018kg and the mass of soda is msoda=0.25kg. Then we calculate the final temperature:
Tf=20,930J−6012J1122J/oC=13oC.
Significance This example illustrates the large energies involved during a phase change. The mass of ice is about 7% of the mass of the soda but leads to a noticeable change in the temperature of the soda. Although we assumed that the ice was at the freezing temperature, this is unrealistic for ice straight out of a freezer: The typical temperature is −6oC. However, this correction makes no significant change from the result we found. Can you explain why?
Like solid-liquid and liquid-vapor transitions, direct solid-vapor transitions or sublimations involve heat. The energy transferred is given by the equation Q=mLs, where Ls is the heat of sublimation, analogous to Lf and Lv. The heat of sublimation at a given temperature is equal to the heat of fusion plus the heat of vaporization at that temperature.
We can now calculate any number of effects related to temperature and phase change. In each case, it is necessary to identify which temperature and phase changes are taking place. Keep in mind that heat transfer and work can cause both temperature and phase changes.
- Examine the situation to determine that there is a change in the temperature or phase. Is there heat transfer into or out of the system? When it is not obvious whether a phase change occurs or not, you may wish to first solve the problem as if there were no phase changes, and examine the temperature change obtained. If it is sufficient to take you past a boiling or melting point, you should then go back and do the problem in steps—temperature change, phase change, subsequent temperature change, and so on.
- Identify and list all objects that change temperature or phase.
- Identify exactly what needs to be determined in the problem (identify the unknowns). A written list is useful.
- Make a list of what is given or what can be inferred from the problem as stated (identify the knowns). If there is a temperature change, the transferred heat depends on the specific heat of the substance (Heat Transfer, Specific Heat, and Calorimetry), and if there is a phase change, the transferred heat depends on the latent heat of the substance (Table 1.6.1).
- Solve the appropriate equation for the quantity to be determined (the unknown).
- Substitute the knowns along with their units into the appropriate equation and obtain numerical solutions complete with units. You may need to do this in steps if there is more than one state to the process, such as a temperature change followed by a phase change. However, in a calorimetry problem, each step corresponds to a term in the single equation Qhot+Qcold=0.
- Check the answer to see if it is reasonable. Does it make sense? As an example, be certain that any temperature change does not also cause a phase change that you have not taken into account.
Why does snow often remain even when daytime temperatures are higher than the freezing temperature?
Snow is formed from ice crystals and thus is the solid phase of water. Because enormous heat is necessary for phase changes, it takes a certain amount of time for this heat to be transferred from the air, even if the air is above 0oC


