1.5: Heat Transfer, Specific Heat, and Calorimetry
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain phenomena involving heat as a form of energy transfer
- Solve problems involving heat transfer
We have seen in previous chapters that energy is one of the fundamental concepts of physics. Heat is a type of energy transfer that is caused by a temperature difference, and it can change the temperature of an object. As we learned earlier in this chapter, heat transfer is the movement of energy from one place or material to another as a result of a difference in temperature. Heat transfer is fundamental to such everyday activities as home heating and cooking, as well as many industrial processes. It also forms a basis for the topics in the remainder of this chapter.
We also introduce the concept of internal energy, which can be increased or decreased by heat transfer. We discuss another way to change the internal energy of a system, namely doing work on it. Thus, we are beginning the study of the relationship of heat and work, which is the basis of engines and refrigerators and the central topic (and origin of the name) of thermodynamics.
Internal Energy and Heat
A thermal system has internal energy (also called thermal energy), which is the sum of the mechanical energies of its molecules. A system’s internal energy is proportional to its temperature. As we saw earlier in this chapter, if two objects at different temperatures are brought into contact with each other, energy is transferred from the hotter to the colder object until the bodies reach thermal equilibrium (that is, they are at the same temperature). No work is done by either object because no force acts through a distance (as we discussed in Work and Kinetic Energy). These observations reveal that heat is energy transferred spontaneously due to a temperature difference. Figure 1.5.1 shows an example of heat transfer.
The meaning of “heat” in physics is different from its ordinary meaning. For example, in conversation, we may say “the heat was unbearable,” but in physics, we would say that the temperature was high. Heat is a form of energy flow, whereas temperature is not. Incidentally, humans are sensitive to heat flow rather than to temperature.
Since heat is a form of energy, its SI unit is the joule (J). Another common unit of energy often used for heat is the calorie (cal), defined as the energy needed to change the temperature of 1.00 g of water by 1.00oC—specifically, between 14.5oC and 15.5oC since there is a slight temperature dependence. Also commonly used is the kilocalorie (kcal), which is the energy needed to change the temperature of 1.00 kg of water by 1.00oC. Since mass is most often specified in kilograms, the kilocalorie is convenient. Confusingly, food calories (sometimes called “big calories,” abbreviated Cal) are actually kilocalories, a fact not easily determined from package labeling.
Mechanical Equivalent of Heat
It is also possible to change the temperature of a substance by doing work, which transfers energy into or out of a system. This realization helped establish that heat is a form of energy. James Prescott Joule (1818–1889) performed many experiments to establish the mechanical equivalent of heat—the work needed to produce the same effects as heat transfer. In the units used for these two quantities, the value for this equivalence is
1.000kcal=4186J. We consider this equation to represent the conversion between two units of energy. (Other numbers that you may see refer to calories defined for temperature ranges other than 14.5oC to 15.5oC.)
Figure 1.5.2 shows one of Joule’s most famous experimental setups for demonstrating that work and heat can produce the same effects and measuring the mechanical equivalent of heat. It helped establish the principle of conservation of energy. Gravitational potential energy (U) was converted into kinetic energy (K), and then randomized by viscosity and turbulence into increased average kinetic energy of atoms and molecules in the system, producing a temperature increase. Joule’s contributions to thermodynamics were so significant that the SI unit of energy was named after him.
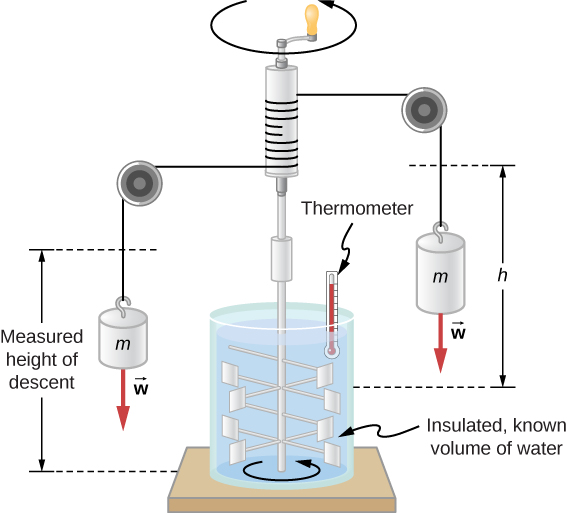
Increasing internal energy by heat transfer gives the same result as increasing it by doing work. Therefore, although a system has a well-defined internal energy, we cannot say that it has a certain “heat content” or “work content.” A well-defined quantity that depends only on the current state of the system, rather than on the history of that system, is known as a state variable. Temperature and internal energy are state variables. To sum up this paragraph, heat and work are not state variables.
Incidentally, increasing the internal energy of a system does not necessarily increase its temperature. As we’ll see in the next section, the temperature does not change when a substance changes from one phase to another. An example is the melting of ice, which can be accomplished by adding heat or by doing frictional work, as when an ice cube is rubbed against a rough surface.
Temperature Change and Heat Capacity
We have noted that heat transfer often causes temperature change. Experiments show that with no phase change and no work done on or by the system, the transferred heat is typically directly proportional to the change in temperature and to the mass of the system, to a good approximation. (Below we show how to handle situations where the approximation is not valid.) The constant of proportionality depends on the substance and its phase, which may be gas, liquid, or solid. We omit discussion of the fourth phase, plasma, because although it is the most common phase in the universe, it is rare and short-lived on Earth.
We can understand the experimental facts by noting that the transferred heat is the change in the internal energy, which is the total energy of the molecules. Under typical conditions, the total kinetic energy of the molecules Ktotal is a constant fraction of the internal energy (for reasons and with exceptions that we’ll see in the next chapter). The average kinetic energy of a molecule Kave is proportional to the absolute temperature. Therefore, the change in internal energy of a system is typically proportional to the change in temperature and to the number of molecules, N. Mathematically, ΔU∝ΔKtotal=NKave∝NΔT. The dependence on the substance results in large part from the different masses of atoms and molecules. We are considering its heat capacity in terms of its mass, but as we will see in the next chapter, in some cases, heat capacities per molecule are similar for different substances. The dependence on substance and phase also results from differences in the potential energy associated with interactions between atoms and molecules.
A practical approximation for the relationship between heat transfer and temperature change is:
Q=mcΔT,
where Q is the symbol for heat transfer (“quantity of heat”), m is the mass of the substance, and ΔT is the change in temperature. The symbol c stands for the specific heat (also called “specific heat capacity”) and depends on the material and phase. The specific heat is numerically equal to the amount of heat necessary to change the temperature of 1.00kg of mass by 1.00oC. The SI unit for specific heat is J/(kg×K) or J/(kg×oC). (Recall that the temperature change ΔT is the same in units of kelvin and degrees Celsius.)
Values of specific heat must generally be measured, because there is no simple way to calculate them precisely. Table 1.5.1 lists representative values of specific heat for various substances. We see from this table that the specific heat of water is five times that of glass and 10 times that of iron, which means that it takes five times as much heat to raise the temperature of water a given amount as for glass, and 10 times as much as for iron. In fact, water has one of the largest specific heats of any material, which is important for sustaining life on Earth.
The specific heats of gases depend on what is maintained constant during the heating—typically either the volume or the pressure. In the table, the first specific heat value for each gas is measured at constant volume, and the second (in parentheses) is measured at constant pressure. We will return to this topic in the chapter on the kinetic theory of gases.
| Substance | Specific Heat (c) J/kg⋅oC | Specific Heat (c) kcal/kg⋅oC|2| |
|---|---|---|
| Solids | ||
| Aluminum | 900 | 0.215 |
| Asbestos | 800 | 0.19 |
| Concrete, granite (average) | 840 | 0.20 |
| Copper | 387 | 0.0924 |
| Glass | 840 | 0.20 |
| Gold | 129 | 0.0308 |
| Human body (average at 37oC) | 3500 | 0.83 |
| Ice (average −50oC to 0oC) | 2090 | 0.50 |
| Iron, steel | 452 | 0.108 |
| Lead | 128 | 0.0305 |
| Silver | 235 | 0.0562 |
| Wood | 1700 | 0.40 |
| Liquids | ||
| Benzene | 1740 | 0.415 |
| Ethanol | 2450 | 0.586 |
| Glycerin | 2410 | 0.576 |
| Mercury | 139 | 0.0333 |
| Water (15.0oC) | 4186 | 1.000 |
| Gases[3] | ||
| Air (dry) | 721 (1015) | 0.172 (0.242) |
| Ammonia | 1670 (2190) | 0.399 (0.523) |
| Carbon dioxide | 638 (833) | 0.152 (0.199) |
| Nitrogen | 739 (1040) | 0.177 (0.248) |
| Oxygen 1.5.1 | 651 (913) | 0.156 (0.218) |
| Steam (100oC) | 1520 (2020) | 0.363 (0.482) |
|
The values for solids and liquids are at constant volume and 25oC, except as noted. [2]These values are identical in units of cal/g⋅oC.[3] Specific heats at constant volume and at 20.0oC except as noted, and at 1.00 atm pressure. Values in parentheses are specific heats at a constant pressure of 1.00 atm. |
||
In general, specific heat also depends on temperature. Thus, a precise definition of c for a substance must be given in terms of an infinitesimal change in temperature. To do this, we note that c=1mΔQΔT and replace Δ with d:
c=1mdQdT.
Except for gases, the temperature and volume dependence of the specific heat of most substances is weak at normal temperatures. Therefore, we will generally take specific heats to be constant at the values given in the table.
A 0.500-kg aluminum pan on a stove and 0.250 L of water in it are heated from 20.0oC to 80.0oC. (a) How much heat is required? What percentage of the heat is used to raise the temperature of (b) the pan and (c) the water?
Strategy
We can assume that the pan and the water are always at the same temperature. When you put the pan on the stove, the temperature of the water and that of the pan are increased by the same amount. We use the equation for the heat transfer for the given temperature change and mass of water and aluminum. The specific heat values for water and aluminum are given in Table 1.5.1.
Solution
- Calculate the temperature difference: Δt=Tf−Ti=60.0oC.
- Calculate the mass of water. Because the density of water is 1000kg/m3, 1 L of water has a mass of 1 kg, and the mass of 0.250 L of water is mw=0.250kg.
- Calculate the heat transferred to the water. Use the specific heat of water in Table 1.5.1: Qw=mwcwΔT=(0.250kg)(4186J/kgoC)(60.0oC)=62.8kJ.
- Calculate the heat transferred to the aluminum. Use the specific heat for aluminum in Table 1.5.1: QA1=mA1cA1ΔT=(0.500kg)(900J/kgoC)(60.0oC)=27.0kJ.
- Find the total transferred heat: QTotal=QW+QA1=89.8kJ.
Significance
In this example, the heat transferred to the container is a significant fraction of the total transferred heat. Although the mass of the pan is twice that of the water, the specific heat of water is over four times that of aluminum. Therefore, it takes a bit more than twice as much heat to achieve the given temperature change for the water as for the aluminum pan.
Example 1.5.2 illustrates a temperature rise caused by doing work. (The result is the same as if the same amount of energy had been added with a blowtorch instead of mechanically.)
Truck brakes used to control speed on a downhill run do work, converting gravitational potential energy into increased internal energy (higher temperature) of the brake material (Figure 1.5.3). This conversion prevents the gravitational potential energy from being converted into kinetic energy of the truck. Since the mass of the truck is much greater than that of the brake material absorbing the energy, the temperature increase may occur too fast for sufficient heat to transfer from the brakes to the environment; in other words, the brakes may overheat.

Calculate the temperature increase of 10 kg of brake material with an average specific heat of 800J/kg⋅C if the material retains 10% of the energy from a 10,000-kg truck descending 75.0 m (in vertical displacement) at a constant speed.
Strategy
We calculate the gravitational potential energy (Mgh) that the entire truck loses in its descent, equate it to the increase in the brakes’ internal energy, and then find the temperature increase produced in the brake material alone.
Solution
First we calculate the change in gravitational potential energy as the truck goes downhill:
Mgh=(10,000kg)(9.80m/s2)(75.0m)=7.35×106J.
Because the kinetic energy of the truck does not change, conservation of energy tells us the lost potential energy is dissipated, and we assume that 10% of it is transferred to internal energy of the brakes, so take Q=Mgh/10. Then we calculate the temperature change from the heat transferred, using
ΔT=7.35×105J(10kg)(800J/kgoC)=92oC.
Significance
If the truck had been traveling for some time, then just before the descent, the brake temperature would probably be higher than the ambient temperature. The temperature increase in the descent would likely raise the temperature of the brake material very high, so this technique is not practical. Instead, the truck would use the technique of engine braking. A different idea underlies the recent technology of hybrid and electric cars, where mechanical energy (kinetic and gravitational potential energy) is converted by the brakes into electrical energy in the battery, a process called regenerative braking.
In a common kind of problem, objects at different temperatures are placed in contact with each other but isolated from everything else, and they are allowed to come into equilibrium. A container that prevents heat transfer in or out is called a calorimeter, and the use of a calorimeter to make measurements (typically of heat or specific heat capacity) is called calorimetry.
We will use the term “calorimetry problem” to refer to any problem in which the objects concerned are thermally isolated from their surroundings. An important idea in solving calorimetry problems is that during a heat transfer between objects isolated from their surroundings, the heat gained by the colder object must equal the heat lost by the hotter object, due to conservation of energy:
Qcold+Qhot=0.
We express this idea by writing that the sum of the heats equals zero because the heat gained is usually considered positive; the heat lost, negative.
Suppose you pour 0.250 kg of 20.0oC water (about a cup) into a 0.500-kg aluminum pan off the stove with a temperature of 150oC. Assume no heat transfer takes place to anything else: The pan is placed on an insulated pad, and heat transfer to the air is neglected in the short time needed to reach equilibrium. Thus, this is a calorimetry problem, even though no isolating container is specified. Also assume that a negligible amount of water boils off. What is the temperature when the water and pan reach thermal equilibrium?
Strategy
Originally, the pan and water are not in thermal equilibrium: The pan is at a higher temperature than the water. Heat transfer restores thermal equilibrium once the water and pan are in contact; it stops once thermal equilibrium between the pan and the water is achieved. The heat lost by the pan is equal to the heat gained by the water—that is the basic principle of calorimetry.
Solution
- Use the equation for heat transfer Q=mcΔT to express the heat lost by the aluminum pan in terms of the mass of the pan, the specific heat of aluminum, the initial temperature of the pan, and the final temperature: Qhot=mA1cA1(Tf−150oC).
- Express the heat gained by the water in terms of the mass of the water, the specific heat of water, the initial temperature of the water, and the final temperature: Qcold=mwcw(Tf−20.0oC).
- Note that Qhot<0 and Qcold>0 and that as stated above, they must sum to zero: Qcold+Qhot=0Qcold=−Qhotmwcw(Tf−20.0C)=−mA1cA1(Tf−150oC).
- This a linear equation for the unknown final temperature, Tf. Solving for Tf, Tf=mA1cA1(150oC)+mwcw(20.0oC)mA1cA1+mwcw, and insert the numerical values: Tf=(0.500kg)(900J/kgoC)(150oC)+(0.250kg)(4186J/kgoC)(20.0oC)(0.500kg)(900J/kgoC)+(0.250kg)(4186J/kgoC)=59.1oC.
Significance Why is the final temperature so much closer to 20.0oC than to 150oC? The reason is that water has a greater specific heat than most common substances and thus undergoes a smaller temperature change for a given heat transfer. A large body of water, such as a lake, requires a large amount of heat to increase its temperature appreciably. This explains why the temperature of a lake stays relatively constant during the day even when the temperature change of the air is large. However, the water temperature does change over longer times (e.g., summer to winter).
If 25 kJ is necessary to raise the temperature of a rock from 25oC to 30oC, how much heat is necessary to heat the rock from 45oC to 50oC?
- Answer
-
To a good approximation, the heat transfer depends only on the temperature difference. Since the temperature differences are the same in both cases, the same 25 kJ is necessary in the second case. (As we will see in the next section, the answer would have been different if the object had been made of some substance that changes phase anywhere between 30oC and 50oC.)
At low temperatures, the specific heats of solids are typically proportional to T3. The first understanding of this behavior was due to the Dutch physicist Peter Debye, who in 1912, treated atomic oscillations with the quantum theory that Max Planck had recently used for radiation. For instance, a good approximation for the specific heat of salt, NaCl, is c=3.33×104Jkg⋅k(T321K)3. The constant 321 K is called the Debye temperature of NaCl, ΘD and the formula works well when T<0.04ΘD. Using this formula, how much heat is required to raise the temperature of 24.0 g of NaCl from 5 K to 15 K?
Solution
Because the heat capacity depends on the temperature, we need to use the equation c=1mdQdT.
We solve this equation for Q by integrating both sides: Q=m∫T2T1cdT.
Then we substitute the given values in and evaluate the integral:
Q=(0.024kg)∫T2T13.33×104Jkg⋅K(T321K)3dT=(6.04×10−6JK4)T4|15K5K=0.302J.
Significance If we had used the equation Q=mcΔT and the room-temperature specific heat of salt, 880J/kg⋅K, we would have gotten a very different value.


